Прогнозирование значений

Анализ данных связан с выработкой прогнозных оценок значений наблюдаемых показателей. Методы прогнозирования учитывают характер процессов. Для установления формы связи факторов модели традиционно используется регрессионно–корреляционный анализ, строится уравнения регрессии.

Процессы с незначительной вариацией средних значений на коротких интервалах времени прогнозируются с помощью метода скользящего среднего. Все наблюдения временного ряда имеют одинаковый «вес» для прогноза. Каждое значение, кроме начальных, участвует в формировании нескольких прогнозных значений:

где - сглаженное значение;- исходное значение;- интервал сглаживания.

Результат прогноза выводится в виде таблицы и графика для сопоставления фактических и прогнозных значений, вычисляется стандартная погрешность для каждой точки ряда Прогноз.

Последовательность действий для прогноза методом скользящего среднего (все исходные данные представлены на рабочем листе):

1. Подготовить вектор–строку или вектор–столбец исходных данных для анализа.

Таблица 15

Год эксплуатации оборудования	Затраты на ремонт, т.руб
1	0,12
2	1,1
3	2,3
4	0
5	0
6	1,1
7	1,8
8	7,8
9	7,1
10	0,67
11	6,75
12	1,75

2. Команда меню СервисАнализ данных – вызов Пакета анализа.

3. Выбор метода Скользящее среднее.

4. Указать параметры:

• Входной интервал – блок ячеек, содержащий исходные значения, – Затраты на ремонт оборудования.

• Флажок Метки в первой строке выбран/не выбран (зависит от выделения входного интервала).

• Интервал – 3 (расчет среднего из 3 смежных значений).

• Выходной интервал – любая ячейка на рабочем листе с данными.

 Выходной диапазон и данные входного диапазона должны быть расположены на одном листе.

• Флажок Вывод графика (если выбран, выводится график для сравнения фактических и прогнозных значений).

• Флажок Стандартные погрешности (если выбран, вычисляются стандартные погрешности прогнозных значений по сравнению с фактическими значениями).

• Нажать кнопку ОК.

На рис. 17 представлена диаграмма скользящего среднего. Очевидна тенденция возрастания затрат на ремонт.

Рисунок 17

Если более поздние значения анализируемых показателей имеют больший «вес» для прогноза, применяется метод экспоненциального сглаживания. Каждое значение ряда участвует в формировании прогнозных значений с переменным «весом», который убывает по мере «устаревания» данных:

• Y_i – прогнозное значение;

• Y_i-1 – прогнозное значение предыдущего периода;

• y_i – фактическое значение;

• α – фактор затухания.

Чем больше α, тем более значимы фактические (последние) данные для прогноза.

Последовательность действий для метода экспоненциального сглаживания:

1. Подготовить вектор–строку или вектор–столбец исходных данных для анализа (см. табл. 15).

2. Команда меню СервисАнализ данных – вызов Пакета анализа.

3. Выбор метода Экспоненциальное сглаживание.

4. Указать параметры:

• Входной интервал – блок ячеек, содержащий исходные значения.

• Флажок Метки в первой строке выбран/не выбран (зависит от выделения входного интервала).

• Фактор затухания – 0,3.

• Выходной интервал – любая ячейка на рабочем листе с данными.

 Выходной диапазон и данные входного диапазона должны быть расположены на одном листе.

• Флажок Вывод графика (если выбран, выводится график для сравнения фактических и прогнозных значений).

• Флажок Стандартные погрешности (если выбран, вычисляются стандартные погрешности прогнозных значений по сравнению с фактическими значениями).

• Нажать кнопку ОК.

На рис. 18 представлена диаграмма экспоненциального сглаживания. Очевидна тенденция возрастания затрат на ремонт.

 Для рассмотренного примера значение экспоненциального сглаживания несколько выше, чем для скользящего среднего.

Рисунок 18

Метод регрессии дает оценку корреляционной зависимости между различными случайными величинами (признаками), среди которых выделяется результативный признак, прочие величины считаются независимыми факторами. Зависимость результативного признака от факторов выражается с помощью коэффициента корреляции.

По числу факторов различают простую (парную) и множественную (несколько факторов) регрессию. Вид и параметры уравнения регрессии устанавливаются с помощью метода наименьших квадратов отклонений фактических данных от выровненных значений. По виду уравнения регрессии различают: линейную и нелинейную.

Статистическая оценка тесноты связи показателя и факторов основана на показателях вариации:

• Общая дисперсия результативного признака, обусловленная влиянием всех факторов в совокупности – ;

• Факторная дисперсия результативного признака, отражающая вариацию результативного признака от воздействия фактора – .

• Остаточная дисперсия результативного признака от воздействия всех прочих факторов, кроме выделенного фактора, – .

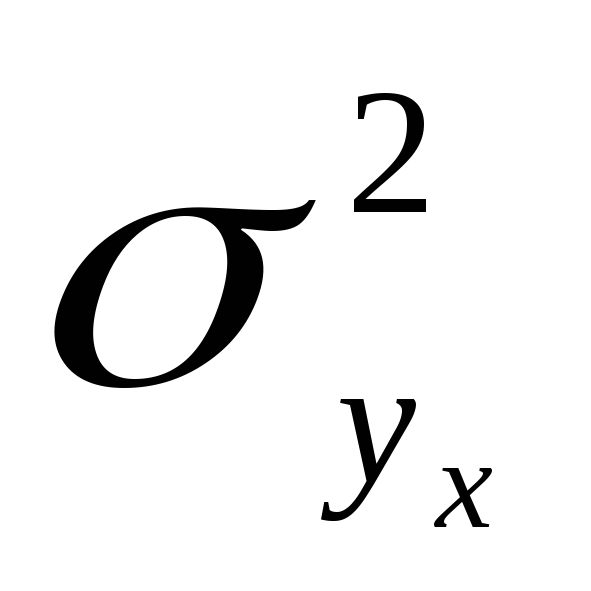Основное соотношение: =+

Коэффициент детерминации – R² вычисляется как отношение факторной дисперсии к общей дисперсии. Индекс корреляции – R.

Для оценки значимости величины R рассчитывается:

где n – размер выборки, m – число факторов.

Используется F-критерий Фишера для определения критического значения приk₁.=m, k₂ = n–m. Вычисленное критическое значение сравнивается с фактическим значением. Если>, величинаR признается существенной. Величинавычисляется с помощью встроенной функцииFРАСПРОБР.

На практике используется порог 0,7: связь считается сильной и уравнение регрессии пригодно для прогнозирования, если R больше 0,7.

Стандартное уравнение парной регрессии линейного вида:

.

Для каждого коэффициента уравнения регрессии вычисляются оценки t-критерия Стьюдента для определения их значимости:

• Стандартная ошибка коэффициента регрессии.

• t-статистика как отношение коэффициента к стандартной ошибке.

Критическое значение t–статистики вычисляется с помощью встроенной функции СТЬЮДРАСПОБР. Если t–статистика значима, коэффициенты принимаются для построения уравнения регрессии, в противном случае – отбрасываются как незначимые факторы.

Последовательность действий:

1. Подготовить исходные данные для анализа – табл. 16.

Таблица 16

Срок эксплуатации оборудования, лет	Выпуск продукции, т.руб./год	Затраты на ремонт, т.руб/год
1,3	1200	0,12
2,1	2100	1,1
4,1	5000	2,3
1	4500	0
0	5000	0
1,75	6000	1,1
2,3	3200	1,8
12,1	1000	7,8
10	6700	7,1
1	1200	0,67
8,6	4300	6,75
3,4	2670	1,75

2. Команда меню СервисАнализ данных – вызов Пакета анализа.

3. Выбрать метод Регрессия.

4. Указать параметры регрессии:

• Входной интервал Y – блок ячеек, содержащий значения результирующего признака – Затраты на ремонт.

• Входной интервал X – блоки ячеек, содержащие значения факторных признаков – Срок эксплуатации и Выпуск продукции.

• Флажок Метки выбран/не выбран (зависит от выделения входного интервала).

• Флажок Константа 0 выбран/не выбран (линия регрессии проходит/не проходит через начало координат).

• Уровень надежности – любой (уровень 95% – по умолчанию).

• Выходной интервал – ячейка листа.

• Флажок Остатки выбран/не выбран (для расчета отклонений прогнозного значения от фактического).

• Флажок Стандартизованные остатки выбран/не выбран.

• Флажок График остатков выбран/не выбран.

• Флажок График подбора выбран/не выбран.

• Флажок График нормальной вероятности выбран/не выбран.

• Нажать кнопку ОК.

Регрессионная статистика для оценки коэффициента детерминации (силы связи результирующего и факторных признаков) приведена в табл. 17. Поскольку коэффициент R-квадрат близок к 1, затраты на ремонт оборудования зависят от срока его эксплуатации и объема выпуска продукции.

Таблица 17

Множественный R	0,985
R-квадрат		0,970
Нормированный R-квадрат		0,867
Стандартная ошибка		0,528
Наблюдения		12

Дисперсионный анализ представлен в табл. 18.

Таблица 18

	Df		SS		MS		F		Значимость F
Регрессия		2		91,030		45,515		163,244		2,57E-08
Остаток		9		2,788		0,279
Итого		11		93,818

Df – число независимых переменных для регрессии, остатка, итого (размерность выборки минус 1).

SS – сумма квадратов отклонений для регрессии, остатка и общая.

MS – дисперсия регрессии и остатка.

F – отношение дисперсии регрессии и дисперсии остатка.

Значимость F – уровень значимости. Уравнение регрессии значимо для прогнозирования, если выражение (1- Значимость F) близко к 1.

Параметры уравнения регрессии представлены в табл. 19 (в данном случае не была задана константа 0).

Таблица 19

	Y-пересечение		Переменная 1		Переменная 2 ….
Коэффициенты		-0,62695		0,718853		8,77E-05
Стандартная ошибка		0,313437		0,034967		7,15E-05
t-статистика		-2,00024		20,55806		1,227356
P-Значение		0,076524		7,12E-09		0,250823
Нижние 95%		-1,33599		0,639752		-7,4E-05
Верхние 95%		0,082096		0,797954		0,000249
Нижние 67,0%		-0,94971		0,682845		1,41E-05
Верхние 67,0%		-0,30418		0,754861		0,000161

Переменная 2 уравнения регрессии не является значимой (остаток 1–P-значение не приближается к 1), поэтому вид уравнения регрессии:

.

Коэффициенты в уравнении регрессии могут выбираться из интервала (верхние, нижние для указанного уровня надежности), например, для 95% :

Различные графики иллюстрируют вычисленные параметры регрессии:

• График подбора – диаграмма типа График (линия), в качестве оси Х используется один из параметров модели. Содержит ряды данных: фактическое и модельное (регрессионное) значение результативного признака.

• График остатков – диаграмма Точечного типа, в качестве оси Х используется один из параметров модели, в качестве ряда – остатки, вычисляемые как разность фактического и прогнозного значения результативного признака.

• График нормального распределения – диаграмма Точечного типа, в качестве оси Х используется персентиль выборки, в качестве оси Y – значения результативного признака.