mathan@answer
.docx
[q]3:1:
Найти
производную функции
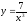
[a][+]
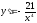
[a]
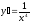
[a]
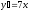
[a]
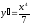
[a]
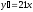
[q]3:1:
Найти
производную функции
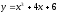
[a][+]
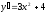
[a]
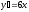
[a]
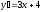
[a]
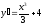
[a]
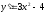
[q]3:1:
Найти
производную функции
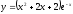
[a][+]
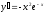
[a]
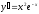
[a]
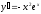
[a]
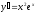
[a] 0
[q]3:1:
Найти
производную функции
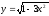
[a][+]

[a]
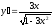
[a]
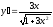
[a]
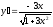
[a]
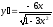
[q]3:1:
Найти
производную функции
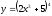
[a][+] 24х2(2х3+5)3
[a] 24х2(2х3-5)3
[a] -24х2(2х3+5)3
[a] 24х2(2х3+5)4
[a] 48х
[q]3:1:
Найти
производную функции
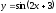
[a][+] 2cos (2x+3)
[a] 2cos (2x-3)
[a] -2cos (2x+3)
[a] cos (2x+3)
[a] -2xcos (2x+3)
[q]3:1:
Найти
производную функции
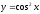
[a][+]
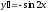
[a]
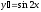
[a]
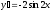
[a]
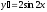
[a]
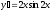
[q]3:1:
Найти
производную функции

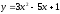
[a][+] 6х-5
[a] -6х+5
[a] -6х-5
[a] 6х+5
[a] 6х2
[q]3:1:
Найти
производную функции
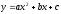
[a][+] 2ax+b
[a] 2ax-b
[a] -2ax+b
[a] -2ax-b
[a] 2ax+b+c
[q]3:1:
Найти
производную функции
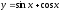
[a][+]

[a]
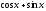
[a]
-
[a]
2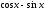
[a]
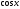
[q]3:1: Найти производную функции (1+2х)30
[a][+] 60(1+2х)29
[a] -6(1+2х)29
[a] -60(1+2х)29
[a] 60(1-2х)29
[a] 60(1+2х)30
[q]3:1: Найти производную функции (1-х2)10
[a][+] -20х(1-х2)9
[a] 20х(1-х2)9
[a] -20х(1+х2)9
[a] 20х(1+х2)9
[a] -20х(1-х2)10
[q]3:1:
Найти
производную функции

[a][+]
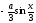
[a]
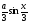
[a]
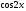
[a]
-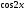
[a] 1
[q]3:1:
Найти
производную функции
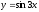
[a][+] 3cos3x
[a] -3cos3x
[a]
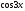
[a]
-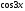
[a] 1
[q]3:1:
Найти
производную функции
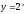
[a][+]
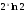
[a]
-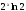
[a] 0
[a]
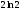
[a] 1
[q]3:1:
Найти
производную функции
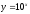
[a][+]
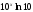
[a]
-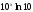
[a] 0
[a]
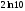
[a] 1
[q]3:1:
Найти
предел:
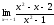
[a][+]
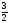
[a] 3
[a] 2
[a] 1
[a] 0
[q]3:1:
Найти
предел:
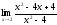
[a][+] 0
[a] 1
[a] 2
[a] 5
[a] 6
[q]3:1:
Найти
предел:
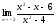
[a][+]
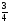
[a] 0
[a] 3
[a] 8
[a] 9
[q]3:1:
Найти
предел:
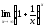
[a][+]

[a] 1
[a]

[a] 0
[a] -1
[q]3:1:
Найти
предел:
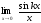
[a][+]
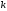
[a] 0
[a] 1
[a]
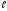
[a] -1
[q]3:1:
Вычислить
интеграл

[a][+]
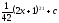
[a]
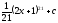
[a]
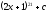
[a]
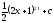
[a]
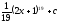
[q]3:1:
Вычислить
интеграл
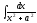
[a][+]
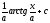
[a]
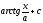
[a]

[a]
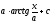
[a]
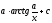
[q]3:1:
Вычислить
интеграл

[a][+]
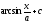
[a]
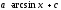
[a]
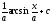
[a]
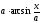
[a]
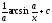
[q]3:1:
Вычислить
интеграл
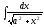
[a][+]
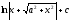
[a]
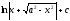
[a]
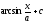
[a]
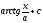
[a]
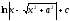
[q]3:1:
Вычислить
интеграл
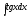
[a][+]
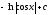
[a]
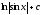
[a]
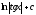
[a]
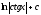
[a]
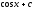
[q]3:1:
Вычислить
интеграл
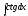
[a][+]
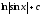
[a]
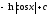
[a]
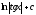
[a]
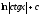
[a]
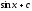
[q]3:1:
Вычислить
интеграл

[a][+]
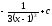
[a]
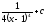
[a]
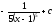
[a]
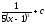
[a]
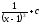
[q]3:1:
Вычислить
интеграл
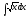
[a][+]
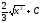
[a]
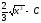
[a]
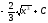
[a]
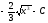
[a]
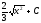
[q]3:1:
Вычислить
интеграл
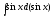
[a][+]
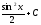
[a] cosx+C
[a]
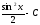
[a]
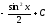
[a] 1
[q]3:1:
Вычислить интеграл
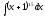
[a][+]
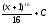
[a]
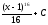
[a]
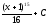
[a]
-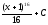
[a] 1
[q]3:1:
Вычислить
интеграл
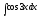
[a][+]
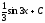
[a]
-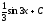
[a]
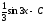
[a]
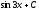
[a] 1
[q]3:1:
Вычислить
интеграл
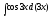
[a][+]
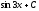
[a]
-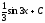
[a]
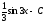
[a]
-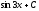
[a] 1
[q]3:1:
Вычислить
интеграл
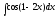
[a][+]
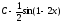
[a]
-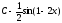
[a]
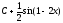
[a]
-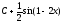
[a] 1
[q]3:1:
Вычислить
интеграл
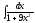
[a][+]
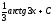
[a]
-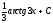
[a]

[a]
-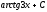
[a] 1
[q]3:1:
Вычислить
интеграл
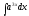
[a][+]
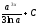
[a]
-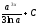
[a]
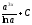
[a]
-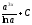
[a] 1
[q]3:1:
Вычислить
интеграл
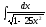
[a][+]
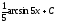
[a]
-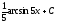
[a]
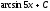
[a]
-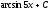
[a] 1
[q]3:1:
Вычислить
интеграл
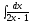
[a][+]
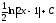
[a]
-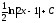
[a]

[a]
-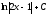
[a] 1
[q]3:1:
Вычислить
интеграл
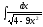
[a][+]
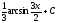
[a]
-
[a]
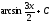
[a]
-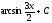
[a] 1
[q]3:1:
Вычислить
интеграл
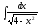
[a][+]
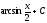
[a]
-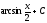
[a]
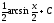
[a]
-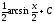
[a] 1
[q]3:1:
Вычислить
интеграл
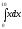
[a][+] 50
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
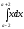
[a][+] 4a
[a] 6a
[a] 7a
[a] 3a
[a] 5a
[q]3:1:
Вычислить
интеграл
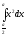
[a][+] 7a3/24
[a] 6a2
[a] 7a2
[a] 3a
[a] 5a
[q]3:1:
Вычислить
интеграл
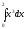
[a][+] 4
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
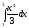
[a][+]
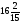
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
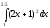
[a][+] 31,5
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
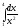
[a][+] 3/4
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
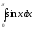
[a][+] 2
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
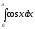
[a][+] 0
[a] 6
[a] 7
[a] 3
[a] 5
[q]3:1:
Вычислить
интеграл
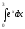
[a][+] e3-1
[a] -e3-1
[a] e3+1
[a] -e3+1
[a] 0
[q]3:1:
Вычислить
интеграл
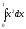
[a][+] 1/3
[a] 6
[a] 7
[a]
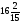
[a] 5
[q]3:1:
Вычислить
интеграл
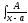
[a][+]
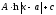
[a]
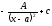
[a]
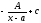
[a]
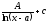
[a]
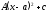
[q]3:1:
Вычислить
интеграл
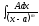 где
где
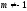
[a][+]
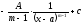
[a]
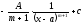
[a]
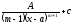
[a]
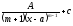
[a]
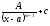
[q]3:1:
найти
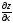 если
если
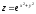
[a][+]
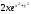
[a]
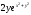
[a]
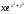
[a]
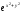
[a]
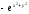
[q]3:1:
Найти
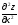 если
если
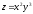
[a][+]
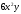
[a]

[a]
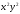
[a]
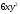
[a] 0
[q]3:1:
Вычислить
интеграл
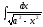
[a][+]
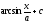
[a]
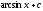
[a]
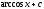
[a]
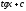
[a]
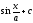
q]3:1:
Найти полный дифференциал функции
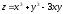
[a][+]
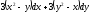
[a]

[a]
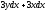
[a]
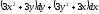
[a]
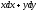
[q]3:1:
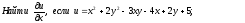
[a][+] 2x-3y-4
[a] 2x+3y-4
[a] 2x-3y+4
[a] 2x+y+4
[a] 0
[q]3:1:
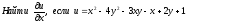
[a][+] 2x-3y-1
[a] 2x+3y-1
[a] 2x-3y+1
[a] 2x+y+1
[a] 0
[q]3:1:
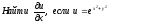
[a][+]
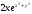
[a]
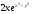

[a]
-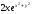
[a]
-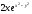
[a] 0
[q]3:1:
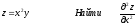
[a][+] 2y
[a] 2x
[a] -2x
[a] -2y
[a] 0
[q]3:1:
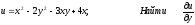
[a][+] -4y-3x
[a] 2x+3y-4
[a] 2x-3y+4
[a] 2x+y+4
[a] 0
[q]3:1:
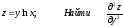
[a][+] 0
[a] -y/x
[a] x/y
[a] -x/y
[a] 1
[q]3:1:
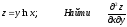
[a][+] 1/x
[a] -y/x
[a] x/y
[a] -x/y
[a] 1
[q]3:1:
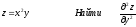
[a][+] 0
[a] 2x
[a] -2x
[a] -2y
[a] 1
[q]3:1: Дифференциальным уравнением называется уравнение в которое неизвестная функция входит:
[a][+] под знаком производной, или дифференциала
[a] под знаком функции у
[a] под знаком производной аргумента х
[a] под знаком дифференциала аргумента х
[a] под знаком аргумента х
[q]3:1: Порядком дифференциального уравнения называется
[a][+] максимальный порядок входящий в уравнение производной, или дифференциала
[a] порядок входящих в уравнение производных
[a] наименьший порядок входящей в уравнение производной
[a] порядок присутствующей производной
[a] сумма порядков присутствующих производных в уравнении
[q]3:1: Дифференциальным уравнением с разделенными переменными называется уравнение
[a][+]
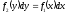
[a]
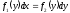
[a]
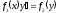
[a]
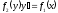
[a]
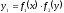
[q]3:1: Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
[a][+]
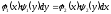
[a]
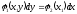
[a]
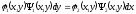
[a]
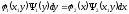
[a]
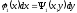
[q]3:1: Линейным дифференциальным уравнением первого порядка называется уравнение
[a][+]
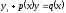
[a]
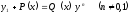
[a]
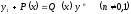
[a]
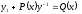
[a]
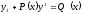
[q]3:1:
Решение линейного дифференциального
уравнения первого порядка
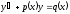 имеет вид:
имеет вид:
[a][+]
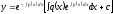
[a]
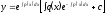
[a]
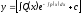
[a]
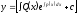
[a]
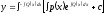
[q]3:1: Уравнение Бернулли имеет вид:
[a][+]
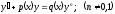
[a]
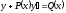
[a]
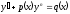
[a]
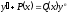
[a]
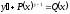
[q]3:1:
Дифференциальное уравнение
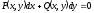 является
уравнением в полных дифференциалах,
если:
является
уравнением в полных дифференциалах,
если:
[a][+]
левая часть является полным дифференциалом,
некоторой функции
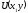
[a]
выполняется условие
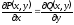
[a]
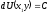
[a]
выполняется условие

[a]
выполняется условие
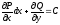
[q]3:1:
Для того, чтобы уравнение
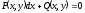 являлось уравнением в полных дифференциалах,
необходимо и достаточно выполнения
условия
являлось уравнением в полных дифференциалах,
необходимо и достаточно выполнения
условия
[a][+]
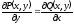
[a]
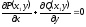
[a]
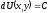
[a]
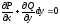
[a]
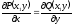
[q]3:1:
Функция
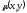 называется
интегрирующим множителем для уравнения
называется
интегрирующим множителем для уравнения
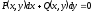 ,
если:
,
если:
[a][+]
уравнение
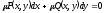 является
уравнением в полных дифференциалах
является
уравнением в полных дифференциалах
[a]
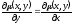
[a]
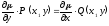
[a]

[a]
выполняется условие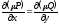
[q]3:1:
Решение уравнения в полных дифференциалах
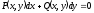 записывается в виде
записывается в виде
[a][+]
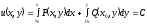
[a]
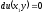
[a]
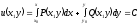
[a]
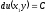
[a]
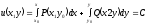
[q]3:1:
Характеристическим уравнением
дифференциального уравнения
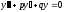 является:
является:
[a][+]
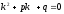
[a]
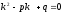
[a]
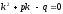
[a]
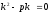
[a]
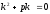
[q]3:1:
Если характеристическое уравнение
дифференциального уравнения
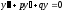 имеет различные действительные корни
имеет различные действительные корни
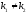 ,
то общее решение запишется в виде:
,
то общее решение запишется в виде:
[a][+]
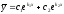
[a]
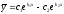
[a]
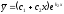
[a]
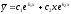
[a]
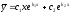
[q]3:1:
Если характеристическое уравнение
дифференциального уравнения
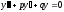 имеет двукратный корень
имеет двукратный корень
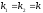 ,
то его общее решение запишется:
,
то его общее решение запишется:
[a][+]
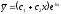
[a]
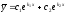
[a]

[a]
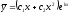
[a]

[q]3:1:
Если характеристическое уравнение
дифференциального уравнения
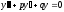 имеет
комплексно-сокращенные корни
имеет
комплексно-сокращенные корни
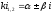 ,
то его общее решение запишется:
,
то его общее решение запишется:
[a][+]
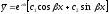
[a]
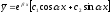
[a]
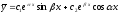
[a]
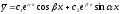
[a]
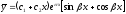
[q]3:1:
Уравнение Бернулли
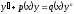 сводится к линейному уравнению с помощью
подстановки
сводится к линейному уравнению с помощью
подстановки
[a][+]
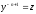
[a]
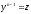
[a]
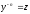
[a]
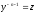
[a]
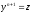
[q]3:1:
Найти общее решение уравнения
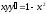
[a][+]
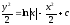
[a]
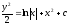
[a]
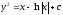
[a]
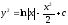
[a]
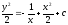
[q]3:1:
Дифференциальное уравнения
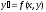 называется
однородным, если выполняется условие:
называется
однородным, если выполняется условие:
[a][+]
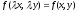
[a]
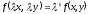
[a]
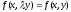
[a]
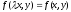
[a]
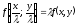
[q]3:1:
Дифференциальное однородное уравнения
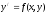 приводится
к уравнению с разделяющимся переменными
с помощью замены:
приводится
к уравнению с разделяющимся переменными
с помощью замены:
[a][+]
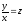
[a]
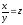
[a]
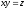
[a]
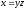
[a]
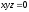
[q]3:1:
Порядок уравнения
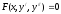 можно
понизить с помощью замены:
можно
понизить с помощью замены:
[a][+]
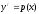
[a]
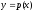
[a]
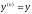
[a]
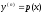
[a]
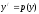
[q]3:1:
Порядок уравнения
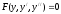 можно понизить с помощью замены:
можно понизить с помощью замены:
[a][+]
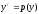
[a]
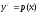
[a]
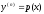
[a]
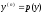
[a]
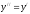
[q]3:1:
Найти общее решение уравнения
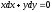
[a][+]
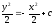
[a]
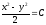
[a]
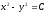
[a]
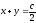
[a]
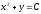
[q]3:1:
Найти общее решение уравнения
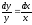
[a][+]
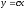
[a]
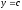
[a]
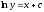
[a]
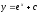
[a]
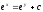
[q]3:1:
Найти общее решение уравнения
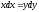
[a][+]
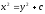
[a]
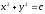
[a]
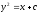
[a]
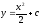
[a]
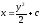
[q]3:1:
Найти общее решение уравнения

[a][+]
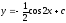
[a]
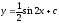
[a]
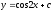
[a]
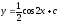
[a]
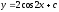
[q]3:1:
Найти общее решение уравнения
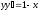
[a][+]
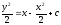
[a]
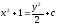
[a]
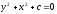
[a]
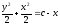
[a]
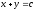
[q]3:1:
Найти общее решение уравнения
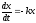
[a][+]
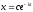
[a]
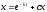
[a]
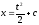
[a]
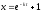
[a]
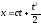
[q]3:1:
Найти общее решение уравнения
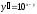
[a][+]
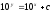
[a]
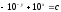
[a]
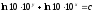
[a]

[a]
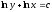
[q]3:1:
Уравнение
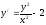 является уравнением
является уравнением
[a][+] однородным
[a] линейным
[a] с разделяющимся переменными
[a] в полных дифференциалах
[a] Бернулли
[q]3:1:
Уравнение
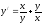 является уравнением
является уравнением
[a][+] однородным
[a] линейным
[a] с разделяющимися переменными
[a] в полных дифференциалах
[a] Бернулли
[q]3:1:
Уравнение
 является
уравнением
является
уравнением
[a][+] линейным
[a] однородным
[a] в полных дифференциалах
[a] Клеро
[a] Бернулли
[q]3:1:
Уравнение
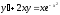 является
уравнением
является
уравнением
[a][+] линейным
[a] однородным
[a] в полных дифференциалах
[a] Клеро
[a] Бернулли
[q]3:1:
Уравнение
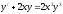 является
уравнением
является
уравнением
[a][+] Бернулли
[a] Клеро
[a] в полных дифференциалах
[a] линейным
[a] однородным
[q]3:1:
Уравнение
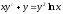 является
уравнением
является
уравнением
[a][+] Бернулли
[a] в полных дифференциалах
[a] Клеро
[a] Лагранжа
[a] однородное
[q]3:1:
Уравнения
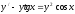 является
уравнением
является
уравнением
[a][+] Бернулли
[a] в полных дифференциалах
[a] Клеро
[a] Лагранжа
[a] однородное
[q]3:1:
Уравнения
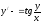 является уравнением
является уравнением
[a][+] однородным
[a] в полных дифференциалах
[a] Бернулли
[a] Клеро
[a] линейным
[q]3:1:
Найти общее решение уравнения
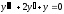
[a][+]
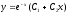
[a]
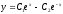
[a]
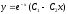
[a]
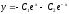
[a]
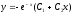
[q]3:1:
Решите дифференциальное уравнение
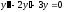 .
.
[a][+]
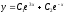
[a]
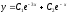
[a]
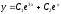
[a]
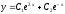
[a]
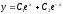
[q]3:1:
Решите дифференциальное уравнение
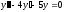 .
.
[a][+]
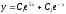
[a]
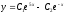
[a]
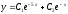
[a]

[a]
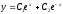
[q]3:1:
Решите дифференциальное уравнение
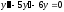 .
.
[a][+]
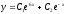
[a]
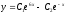
[a]
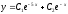
[a]
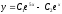
[a]
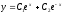
[q]3:1:
Решите дифференциальное уравнение
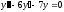 .
.
[a][+]
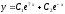
[a]
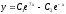
[a]
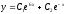
[a]
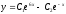
[a]
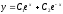
[q]3:1:
Решите дифференциальное уравнение
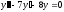 .
.
[a][+]
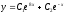
[a]
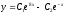
[a]
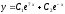
[a]
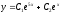
[a]
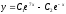
[q]3:1:
Решите дифференциальное уравнение
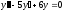 .
.
[a][+]
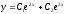
[a]
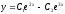
[a]

[a]
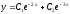
[a]
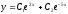
[q]3:1:
Решите дифференциальное уравнение
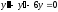 .
.
[a][+]

[a]
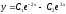
[a]
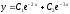
[a]
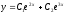
[a]
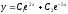
[q]3:1:
Решите дифференциальное уравнение
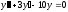 .
.
[a][+]
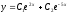
[a]
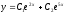
[a]
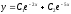
[a]

[a]
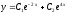
[q]3:1:
Вычислить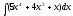
[a][+]
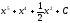
[a]
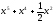
[a]
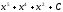
[a]
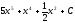
[a]
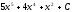
[q]3:1:
Вычислить производную функции:
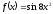
[a][+]