3.11 Синтез астатических систем

Одно из важных требований, предъявляемых к системам регулирования, заключается в том, чтобы постоянное входное воздействие отрабатывалось без установившейся ошибки. Для статических систем при классическом синтезе этого можно добиться с помощью включения ПИ-регулятора.

Аналогичный подход можно использовать и при синтезе путем размещения полюсов. Разумеется, введение в систему ПИ-регулятора будет увеличивать ее порядок на единицу: если порядок объекта равен n, то система будет иметь порядок.

Будем считать, что синтезируемая система имеет структуру, изображенную на рис.3.29. Тогда передаточная функция от кравна

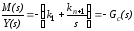, (3-86)

где через обозначена передаточная функция ПИ-регулятора. При необходимости коэффициентможет быть введен в прямую цепь параллельно с интегратором и коэффициентом; характеристическое уравнение системы при этом не изменится.

На рис.3.29 уравнения состояния объекта имеют вид:

, (3-87)

.

Уравнение для интегратора:

. (3-88)

Входной сигнал объекта:

. (3-89)

Составляющие векторов ивыбираются исходя из желаемого размещения полюсов передаточной функции замкнутой системы. Процедура синтеза заключается в следующем. Подставляя (3-89) в (3-87), получим:

. (3-90)

Затем мы объединим переменную с вектороми образуем таким способом вектор состояния системы с обратной связью. Тогда на основании (3-87), (3-88) и (3-90) можно записать:

(3-91)

Этому уравнению можно придать иную форму:

(3-92)

где

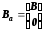,,. (3-93)

Уравнению (3-92) соответствует характеристическое уравнение , которое имеет стандартную форму, используемую при синтезе систем путем размещения полюсов. Характеристическое уравнение имеет порядок; следовательно, желаемое характеристическое уравнениемы должны задать в виде:

. (3-94)

Таким образом,

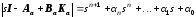. (3-95)

В данном уравнении значенийизвестны, а неизвестным являетсякоэффициент. Для их определения можно либо в (3-95) приравнять коэффициента при одинаковых степеняхв левой и правой части и получить таким образом систему излинейных уравнений, либо воспользоваться формулой Аккермана. Формула Аккермана для решения уравнения (3-95) имеет вид:

. (3-96)

После определения значения формируются обратные связи по компонентам вектора. При этом следует убедиться, что математическая и физическая модель представлены в одном базисе. Часто математические модели задаются в формеtf(передаточные функции). ВMatLabимеется командаss, которая позволяет от формыtfперейти к уравнениям системы, заданным в формеss(матричные уравнения). Однако пользоваться командойssследует осторожно, так какMatLab, за исключением командыcanon, сам выбирает базис, в котором определяются матрицы, и поэтому элементы матрицы, полученные путем преобразования исходной передаточной функции командойss, могут не соответствовать элементам матрицыфизической модели. Например, в физической модели координатахарактеризует ток двигателя, а в математической модели координатаможет и не характеризовать ток двигателя.

Поэтому для определения компонент вектора матричные уравнения системы регулирования следует получать из физической модели.

Пример 3.20.

Разберем эти положения на конкретном примере. Как известно, двигатель постоянного тока независимого возбуждения описывается следующей системой уравнений

, (3-97)

, (3-98)

, (3-99)

, (3-100)

где, - напряжение якоря (вход);- противо ЭДС;- ток якорной цепи;- вращающий момент;- угол поворота вала двигателя;- угловая скорость (выход).

В качестве переменных состояния выберем и. Эти переменные легко поддаются измерению и обычно системы проектируются таким образом, что по этим координатам реализуются обратные связи.

Подставляя уравнение (3-99) в (3-100), получим:

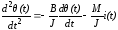
или

.

Из уравнений (3-97) и (3-98) имеем:

.

Выход системы . Следовательно, уравнения состояния принимают вид:

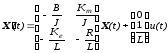, (3-101)

.

Для придания расчетам конкретных значений принимаем, что Гн;Ом;Н∙м/а;В∙с;кг∙м²;Н∙м∙с;В∙об/мин. В систему управления двигателя входит усилитель мощности с коэффициентом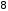. С учетом численных значений матрицы коэффициентов принимают вид:

Заметим, что полученная модель не соответствует ни одной из канонических форм, но зато фазовые координаты модели совпадают с измеряемыми координатами физической системы. Ошибки в выборе базиса приводят к певерным результатам. Этому вопросу будет уделено боль внимания при синтезе дискретных систем.

Предположим, что замкнутая система должна иметь время установления ; тогда постоянная времени должна равняться; а желаемое характеристическое уравнения системы имеет вид

.

Запишем на основании (3-93) расширенные матрицы с учетом уравнений состояния объекта:

,.

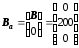Тогда

а характеристический полином, согласно (3-95),

Отсюда определяем неизвестные коэффициенты:

;

Синтез можно проверить с помощью программы MatLab, в которой использована формула Аккермана.

Пример 3.21.

%---------Начало программы Pr_03_21---------

%Формирование матриц Aa, Ba по исходным уравнениям

Aa=[-2.5,1,0;-0.75,-0.5,0;1,0,0];%Исходные данные

Ba=[0;200;0]; %Исходные данные

Pp=[-5,-5,-5]; %Корни замкнутой системы

Ka=acker(Aa,Ba,Pp); %Применение формулы Аккермана

B=[0;0;-1];C=[1,0,0];D=0; %Матрица коэффициентов замкнутой

c10=ss((Aa-Ba*Ka),B,C,D); %системы.

c11=tf(c10) %Переход от формы SS к форме TF.

step(c11) %Переходная функция.

Передаточную функцию замкнутой системы по структуре рис.3.27 (интегральный регулятор) можно определить с помощью командыtfили через характеристическое уравнение замкнутой системы

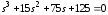. (3-102)

Учитывая единичную обратную связь, из уравнения (3-102) получим

Как отмечалось выше, коэффициент 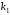можно ввести в цепь параллельно интегратору. При таком соединении в системе будет реализован ПИ-регулятор. Так как характеристическое уравнение замкнутой системы и величина коэффициентаостанутся неизменными (изменяются коэффициентыиза счет изменения структуры), то имеется возможность определить новые значения коэффициентовииз соотношения:

,

,

.

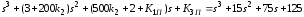Используя значения и, запишем передаточную функцию замкнутой системы с ПИ-регулятором

Переходные функции для двух реализаций системы приведены на рис.3.30. Во втором случае, при передаточной функции , реакция быстрее, т.к. имеется канал прямой передачи от ступенчатой входной функции к напряжению, подаваемому на двигатель. В первом же случае, при передаточной функции, ступенчатая функция интегрируется, так что напряжение, подаваемое на двигатель, в начале процесса аппроксимируется линейной функцией. На практике можно использовать обе реализации; первая из них предпочтительнее тогда, когда нежелательно подвергать объект «удару» со стороны ступенчатого воздействия.