3.10. Сравнительная характеристика методик определения коэффициентов регуляторов в разных базисах

При определении коэффициентов регулятора используется преобразование подобия. В зависимости от исходных данных предложено несколько подходов к определению коэффициентов регуляторов.

1.Уравнение системы регулирования задано в форме УКП, а уравнение наблюдателя задано в форме ИКП. В этом случае целесообразно использовать частные случаи преобразования подобия, связанные со свойствами матриц заданных в базисах УКП и ИКП.

2.Уравнение системы задано в произвольном базисе и его надо привести к канонической форме (УКП и ИКП), используя общую формулу преобразования базисов.

Синтезируемые этими методиками регуляторы будут иметь одну и ту же передаточную функцию, но их структурные схемы будут иметь разное представление. Поэтому для исключения ошибок, которые могут возникнуть при реализации структурных схем регуляторов, рассмотрим более подробно вопросы синтеза систем, обращая внимание на согласование базисов.

1. Пусть система задана в произвольном базисе. По паре матриц 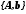определяем матрицу(исходные данные для пределяем матрицу перехода)

.

2. Используя характеристическое уравнение или передаточную функцию системы, определяем пару матриц в форме УКП, а затем вычисляем матрицу(исходные данные для пределяем матрицу перехода)

.

Считаем, что система управляема и наблюдаема. Поэтому матрицы иимеют полный ранг.

3. Определяем матрицу обратную матрице

.

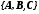4. Определяем матрицу перехода , которая преобразует матрицы, заданные в произвольном базисе, к представлению, заданному в форме УКП

.

5. По известной матрице перехода от произвольного базиса к базису в форме УКП определяем все матрицы системы в форме УКП

:

6. Определяем матрицу перехода от формы УКП к форме ИКП

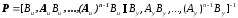
Учитывая, что , а, то имеются все данные для определения матрицы перехода

7. С помощью матриц иосуществляем переход всех векторов от базиса УКП к базису ИКП.

Приведенная последовательность преобразования матриц обоснована для общего случая. Если исходные данные заданы в форме УКП, что часто имеет место, то нет необходимости определять матрицу . Исходные данные для определения матрицывычисляются по известному вектору,и матрице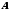, заданными в форме УКП.

Пример 3.17.

Исходная система задана уравнениями

,,.

Требуется, с использованием наблюдателя полного порядка, синтезировать систему регулирования.

Предположим, что по условию синтеза необходимо получить 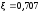, а время установления, т.е.

,.

В этом случае динамические свойства системы будут определяться характеристическим уравнением

.

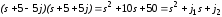Переходные процессы в наблюдателе должны заканчиваться в (2-4) раза быстрее, чем переходные процессы в системе. Принимаем, постоянную времени наблюдателя с., а. Тогда получим

.

Решим этот пример, используя преобразование подобия. Так как пара матриц задана в базисе УКП и известно характеристическое уравнение исходной системы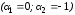, то компоненты векторасразу определяются по формулам

,;.

Для заданного характеристического многочлена, получаем

.

Вектор наблюдателя определяем в базисе ИКП. Переход от формы УКП к форме ИКП осуществляется через матрицыи(смотри пункты 6 и 7).

Можно получить пару матриц 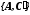в форме ИКП, используя свойство:

где - матрицы заданные в базисе ИКП;- матрицы заданные в базисе УКП.

Так как пара матриц задана в форме ИКП и известно характеристическое уравнение наблюдателя, из которого можно получить матрицу коэффициентов наблюдателя в форме ИКП, то компоненты вектораопределяются из матричного соотношения

. (3-73)

где - матрица коэффициентов исходной системы;- матрица коэффициентов, определяющая динамику наблюдателя.

Подставляя исходные данные в (3-73), получим

,

.

Таким образом, вектор определен в базисе УКП, векторопределен в базисе ИКП. Для правильного функционирования системы запишем все вектора в базисе ИКП.

Преобразования выполняем с помощью матриц 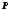и

,;

,;

,.

Таким образом, все матрицы и вектора записаны в одном базисе (форма ИКП), что позволяет определить динамику системы с наблюдателем полного порядка

. (3-74)

Подставляя численные значения в (3-74), имеем

(3-75)

Рис.3.21. Структурная схема системы с наблюдателем полного порядка для примера 3.17.

По уравнениям (3-75) в MatLabсоставлена структурная схема и вSimulink

исследованы динамические характеристики системы с наблюдателем полного порядка (рис.3.21).

Пример 3.18.

Используя данные примера 3.17, решим задачу, применив формулу Аккермана. Запишем выражение, определяющее матрицу обратных связей

. (3-76)

Находим все составляющие, входящие в выражение (3-76)

,

.

Определяем матричный полином

Затем применяем формулу Аккермана

Запишем выражение, определяющее матрицу наблюдателя

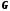
Затем определим матричный полином

.

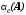
Подставляем исходные данные в формулу Аккермана и получим

Для уравнения наблюдателя

определим входящие в него матрицы

,

,

,

В результате преобразований получим, что регулятор-наблюдатель описывается следующими матричными уравнениями

(3-77)

По уравнениям (3-77) в MatLabсоставлена структурная схема и вSimulinkисследованы динамические характеристики системы (рис.3.20).

Сравнение результатов моделирования структурных схем, представленных на рис.3.21 и рис.3.22 показывают идентичность их динамических характеристик, хотя коэффициенты регуляторов и матричные уравнения систем регулирования различны. Это объясняется тем, что при расчетах с помощью формул Аккермана результаты представлены в базисе УКП, а при расчете вторым методом – в базисе ИКП. Различия в базисах приводит к изменениям внутренних связей внутри блока, но не влияет на характеристики вход – выход. Следовательно, результаты расчета вне зависимости от используемого базиса будут иметь один и тот же набор собственных чисел, а регулятор – наблюдатель будет иметь одну и ту же передаточную функцию, хотя внутренняя структура будет зависеть от выбранного базиса.

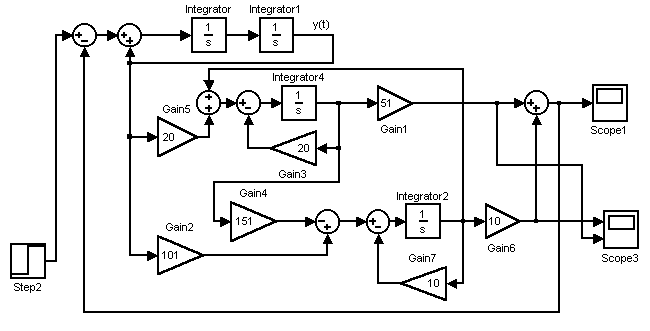
Рис.3.22. Структурная схема системы с наблюдателем полного порядка для примера 3.18.

Сравнение структурных схем наблюдателей, представленных на рис.3.21 и рис.3.22. показывают, что при одинаковых требованиях к динамическим характеристикам собственно системы регулирования и наблюдателя, структурные схемы наблюдателей имеют разный вид, что объясняется различием базисов, в которых синтезировались наблюдатели.

При синтезе было принято, что коэффициент демпфирования системы равен , а коэффициент демпфирования наблюдателя -1. При таких жестких требованиях в системе наблюдается большое перерегулирование. Это свойственно всем системам, использующие наблюдатели для оценки переменных состояния объекта.

Посмотрим, как изменятся динамические показатели системы примера 3.17, если принять коэффициент демпфирования системы . Тогда корни характеристического уравнения должны быть равны

что соответствует характеристическому уравнению

,

;

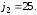
Так как динамика наблюдателя не изменилась, то коэффициенты иостались прежними. Изменение динамики системы будет связано только с изменением коэффициентови.

Подставляя новые значения коэффициентов ив выражение (3-77), получаем

.

Тогда запишем

.

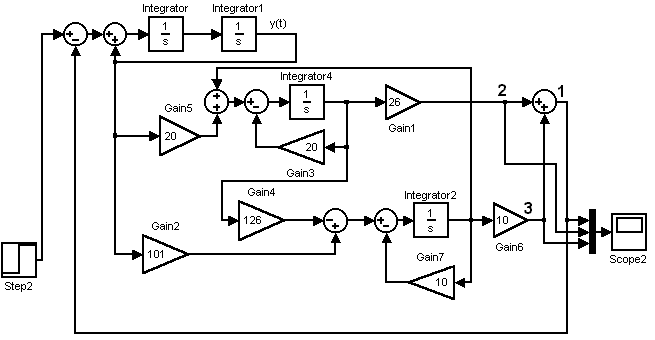
Рис.3.23. Структурная схема системы с наблюдателем полного порядка, в которой изменился коэффициент демпфирования примера 3.18.

Рис.3.24. Результаты моделирования систем по структуре 3.23 (1-выходная координата системы, 2- выход координаты X1, 3- выход координатыX2).

Система регулирования примера 3.18 с измененными требованиями, приводящими к изменению матрицы 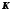, описывается следующими матричными уравнениями

(3-78)

По уравнениям (3-78) в MatLabсоставлена структурная схема (рис.3.23) и вSimulinkисследованы ее динамические характеристики (рис.3.24). Результаты моделирования показывают, что уменьшение коэффициента демпфирования несколько уменьшило величину перерегулирования (кривая 1). Но общая картина осталась неудовлетворительной: величина перерегулирования составляет 40 % и не соответствует требованиям, заложенным в систему. При коэффициенте демпфирования равным единице система вообще не должна иметь перерегулирования.

Пример 3.19.

В данном примере используются исходные данные примера 3.17, но синтезируется наблюдатель пониженного порядка.

Предположим, что постоянная времени наблюдателя . Тогда характеристическое уравнение наблюдателя имеет вид

. (3-79)

Сравнивая уравнения состояния объекта с уравнениями (3-42), имеем

Подготовим исходные данные для формулы Аккермана

тогда на основании (3-57) получим:

После подстановки матриц и коэффициентов получим уравнение первого порядка:

или

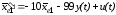. (3-80)

Оценку координаты получим на основании уравнения

.

Так как динамические свойства системы примера 3.19 совпадают с динамическими свойствами системы примера 3.17, то матрица коэффициентов не изменилась

.

(3-81)

По уравнениям (3-80) и (3-81) в MatLabсоставлена структурная схема и вSimulinkисследованы её динамические характеристики (рис.3.25).

Рис.3.25.Структурная схема системы с наблюдателем пониженного порядка

На рис.3.26 представлены переходные характеристики системы

Рис.3.26. Переходные характеристики системы (рис.3.25) по выходным координатам (1- выходная координата системы, 2- выход по координате X1, 3- выход по координатеX2).

Хотя требования к динамическим характеристикам систем с наблюдателями полного и пониженного порядка были одинаковыми, их переходные функции получились разными. В системах с наблюдателем пониженного порядка величина регулирования составила 20 %, что 2 раза меньше, чем в системе с наблюдателем полного порядка.

Определим структурную схему наблюдателя пониженного порядка примера 3.19, используя общую формулу преобразования базисов (формулу Аккермана). В примере 3.17 был определен вектор управления и с помощью преобразования подобия записаны все матрицы в форме ИКП

(3-82)

Учитывая, что динамические свойства наблюдателя заданы уравнением (3-79), запишем матрицу преобразования

;. (3-83)

Применяя (3-83) к матрицам (3-82) получим исходные данные для расчета системы с наблюдателем пониженного порядка

(3-84)

Используя числовые данные предыдущих примеров , получим:

матрицу наблюдателя

вектор управления

вектор обратных связей (3-85)

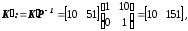
вектор выхода

По уравнениям (3-85) в MatLabсоставлена структурная схема и вSimulinkисследованы её динамические свойства (рис.3.27).

Рис.3.27.Структурная схема системы с наблюдателем пониженного порядка, синтезированным методом согласования базисов

На рис.3.25 и рис.3.27 представлены структурные схемы с наблюдателями пониженного порядка, которые по выходной координате системы (кривая 1 на рис.3.26 и рис.3.28) имеют одинаковые динамические характеристики. Однако структура наблюдателя и коэффициенты обратных связей у них разные. Больше того, у них разные переходные функции по фазовым координатам системы. Это связано с тем, что каждый метод расчета в пространстве состояния определяет свой базис (систему координат). Очевидно, предпочтение следует отдать базису, в котором восстановленные координаты совпадают с координатами реальных систем.

Рис.3.28. Переходные характеристики системы (рис.3.27) по выходным координатам (1- выходная координата системы, 2- выход по координате X1, 3- выход по координатеX2).

Согласно постановке задачи, исследовались уравнения, описывающие процессы в двигателе постоянного тока с наблюдателем, восстанавливающем координату тока. Сравнения кривых (рис.3.26 и рис.3.28) показывает, что при одинаковых выходных характеристиках (кривая 1), переходные характеристики по фазовым координатам различны. Для инженера важно синтезировать наблюдатель в таком базисе, в котором совпадали бы переходные процессы в физической системе и модели. Этим требованиям соответствует наблюдатель, представленный на рис.3.25: координата X1 (кривая 2) восстанавливает ток в физической системе.