11.2. Управляемость и наблюдаемость

Понятие управляемости связано, при подаче непрерывного управляющего воздействия , с переводом систем из некоторого начального состоянияв конечное состояниеза конечное время.

Понятие наблюдаемости связано с оценкой состояния системы в момент времени по известным входными выходнымвоздействиям, приложенным к системе ().

Это первые вопросы, которые следует рассмотреть при проектировании систем, и при их положительных решениях можно приступать к дальнейшим исследованиям. В данном изложении вопросы наблюдаемости и управляемости рассматриваются после исследования систем регулирования.

Отход от общепринятых методик изложения материала объясняется тем, что условия управляемости и наблюдаемости в традиционных учебных курсах вводятся без доказательства, а в данном изложении понятие управляемости и наблюдаемости получено как следствие применения формулы Аккермана.

Управлять системой – это иметь возможность получить заданный переходной процесс, т.е. синтезировать систему на основе требуемого размещения полюсов. Поэтому можно утверждать, что система управляема, когда удается разместить полюсы в заданных точках, т.е. выполнить преобразование матриц по формулам Аккермана

.

Матрица определена тогда, когда матрицаимеет себе обратную, что достигается при выполнении одного из условий:

- определитель этой матрицы не равен нулю;

- ранг этой матрицы должен быть равенn(n- степень характеристического уравнения системы).

MatLabимеет команды, которые определяют ранг матрицы и раскрывают определитель.

Наблюдать систему – это иметь возможность синтезировать наблюдатель на основе размещения полюсов. Поэтому можно утверждать, что система наблюдаема, когда удается разместить полюсы в заданных точках, т.е. выполнить преобразования Аккермана

.

Матрица будет определена только тогда, когда матрица

имеет обратную, т.е. её ранг равен или её определитель не равен нулю.

Если матрица не существует, то объект не управляем, и полюсы замкнутой системы не могут быть размещены в заданных точках. Если матрицане существует, то объект не наблюдаем, и нельзя синтезировать наблюдатель, который оценивал бы все переменные состояния объекта.

Рассмотрим понятия управляемости с позиций классической теории автоматического управления на примере структурной схемы, изображенной на рис.11.5.

Заметим, что полюс датчика совпадает с нулем объекта. Характеристическое уравнение системы имеет вид:

(11.24.)

или

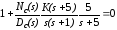.(11.25.)

Чтобы представить характеристическое уравнение в виде полинома, умножим (11.25.) на знаменатель дроби:

,

или

. (11.26.)

Однако, если в (11.25.) сократить члены перед умножением выражения на знаменатель, то характеристическое уравнение примет вид второго сомножителя в (11.26.)

. (11.27.)

Следовательно, мы получили два разных характеристических уравнения, (11.26.) и (11.27.), для одной и той же системы.

Для выражения (11.26.) переходной процесс, определяемый общим решением однородного линейного уравнения, имеет составляющую , а в выражении (11.27.) эта составляющая отсутствует. Поэтому на эту составляющую нельзя воздействовать входным сигналом и с помощью регулятора не удается сдвинуть данный корень характеристического уравнения в заданную точку. Это свидетельствует о том, что данная система по этой координате неуправляема.

Пример 11.5.

Предположим, имеется система, заданная уравнениями пространства состояния

.

Сначала произведем анализ управляемости:

и

.

Таким образом, получим

.

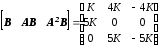Поскольку третий столбец этой матрицы равен второму столбцу с точностью до знака, то определитель матрицы равен нулю и, следовательно, обратной матрицы не существует. Следовательно, система является неуправляемой.

Теперь исследуем наблюдаемость относительно выходной переменной датчика, которая определяется уравнением:

.

Тогда

и

.

Окончательно имеем

.

Определитель этой матрицы равен 25, следовательно, обратная матрица существует, а значит, система является наблюдаемой.

Приведенные вычисления проверяются с помощью следующей программы MatLab.

Пример 11.5.

%-----------Начало программы Pr_03_14--------

А=[-1 1 0; 0 0 0; 5 0 -5]; %Исходные данные

В=[1; 5; 0]; С=[О О 1]; %Исходные данные

Со=ctrb(А, В) %Формирование матрицы управляемости Со.

det(Со), pause %Определение определителя матрицы Со.

Оb=obsv(А, С) %Формирование матрицы наблюдаемости Ob.

det(Оb) %Определение определителя матрицы Ob.

По команде ctrbвычисляется матрица управляемости, а по командеobsv— матрица наблюдаемости, а затем путем определения ранга этих матриц определяется управляемость и наблюдаемость систем регулирования. В большинстве систем, являющихся либо неуправляемыми, либо ненаблюдаемыми, либо и то и другое, происходит сокращение нуля и полюса.

Следовательно, в результате такого сокращения модель системы имеет более низкий порядок. Система, в которой число переменных состояния больше, чем ее минимальный порядок, будет либо неуправляемой, либо ненаблюдаемой, либо и то и другое. Для примера рассмотрим

электрическую схему, изображенную на рис.11.6. Для этой схемы справедливы следующие уравнения:

Эти уравнения можно привести к стандартной форме уравнений состояния:

По этим уравнениям запишем матрицы и:

,.

Следовательно,

,

и матрица управляемости принимает вид:

.

Определитель этой матрицы равен нулю, следовательно, система неуправляема.

Заметим, что в рассмотренной нами схеме две параллельные -ветви могут быть объединены в одну цепь с сопротивлениеми индуктивностью. Поэтому передаточная функция от входного напряжения к токуравна

.

Она имеет первый порядок, тогда как модель схемы в переменных состояния второй, что и определяет неуправляемость схемы.

Целесообразно отметить, что проблемы управляемости и наблюдаемости сформулированы относительно моделей, у которых можно достигнуть полного сокращения нулей и полюсов. Реальная система отличается от её математической модели и в ней не удается достичь полного сокращения нулей и полюсов. Они могут быть компенсированы только приблизительно. Но даже при приблизительной компенсации трудно влиять на свойства системы по приблизительно компенсируемым координатам или оценивать их.