ЛЕКЦИЯ_11. Синтез наблюдателей пониженного порядка

Содержание

11.1. Синтез наблюдателя, оценивающего переменные состояния, которые не могут быть измерены

11.2. Управляемость и наблюдаемость

11.3. Синтез системы при наличии входных воздействий

11.1. Синтез наблюдателя, оценивающего переменные состояния, которые не могут быть измерены. Наблюдатель, рассмотренный в предыдущем разделе, можно назвать наблюдателем полного порядка, т.к. с его помощью мы получаем оценки всех переменных состояния объекта. Однако обычно некоторые из этих переменных состояния доступны для измерения. Например, для двигателя измеряемой координатой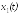является перемещение. Очевидно, что измерение переменной состоянияв этом случае будет более точным, нежели оценка этой переменной с помощью наблюдателя. Поэтому в большинстве случаев нелогично оценивать те переменные состояния, которые можно измерить. Единственным исключением является случай, когда измерение сопровождается большим шумом. В этом случае может оказаться использование оцениваемой переменной обоснованной, так как на измеряемую координату объекта действует помеха, и ошибки фильтрации могут превзойти ошибки оценивания.

По указанным причинам целесообразно синтезировать наблюдатель, дающий оценку только тех переменных состояния, которые не могут быть измерены. Подобное устройство называют наблюдателем пониженного порядка. Определим уравнения, позволяющие синтезировать такой наблюдатель. Причем для конкретности ограничимся случаем измерения переменной состояния 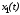. Это ограничение не является существенным, так как изменением матрицыможно измерить любую координату объекта.

При измерении 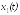уравнение выхода всегда будет иметь вид:

.

Сначала мы разделим вектор состояния на составляющие:

,

где - вектор состояния, подлежащий оценке. Затем мы разделим уравнения состояния:

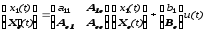. ( 11.1.)

На основании (11.1.) запишем уравнения относительно переменных состояния, подлежащих оценке:

,(11.2.)

а также уравнение относительно измеряемой переменной:

, (11.3.)

В этих уравнениях 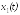и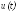известны, а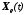неизвестно и подлежит оценке.

Чтобы получить уравнения наблюдателя, преобразуем (11.2.) и (11.3.) в ту же форму, что и уравнения объекта при полной оценке состояния. Поскольку уравнение наблюдателя полного порядка известно, то запишем уравнение наблюдателя пониженного порядка, а затем сравним их. Для наблюдателя полного порядка

(11.4.)

а для наблюдателя пониженного порядка, согласно (11.2.),

. (11.5.)

При полной оценке состояния

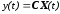, (11.6.)

а для наблюдателя пониженного порядка, согласно (11.3.),

. (11.7.)

Сравнивая (11.4.) с (11.5.) и (11.6.) с (11.7.), обнаружим, что эти уравнения эквивалентны, если сделать следующие замены:

,

,

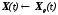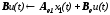, (11.8.)

,

.

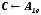Произведя эти подстановки в уравнение наблюдателя полного порядка (10-17),

,

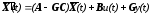получим уравнение наблюдателя пониженного порядка:

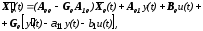(11.9.)

где 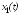заменено на, а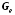есть матрица коэффициентов наблюдателя пониженного порядка. Тогда из (10-20) следует, что динамика изменения ошибки определяется уравнением:

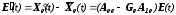. (11.10.)

Следовательно, характеристическое уравнение для наблюдателя и ошибок оценки имеет вид:

. (11.11.)

Если задать полином , определяющий желаемую динамику процесса оценки состояния, то можно найти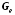, удовлетворяющую данному уравнению.

Используя формулу Аккермана для наблюдателя полного порядка (11-27)

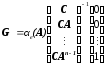, (11.12.)

и произведя замены, определяемые соотношениями (11.8.), получим формулу для синтеза наблюдателя пониженного порядка [10]:

. (11.13.)

Заметим, что порядок этого наблюдателя на единицу меньше, чем порядок наблюдателя полного порядка.

Предыдущие уравнения могут быть использованы для синтеза наблюдателя пониженного порядка, однако при этом существует одна проблема. Как следует из (11.9.), на вход такого наблюдателя должна подаваться производная сигнала . Хотя в принципе можно создать устройства, обладающие дифференцирующими свойствами (например, ПИ-регулятор), однако дифференциатор будет усиливать любой высокочастотный шум, содержащийся в сигнале, что не желательно. Можно исключить необходимость дифференцирования, изменив переменные состояния так, что вычисления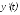не потребуется. Сначала введем новую переменную, которую обозначим:

, (11.14.)

или

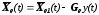(11.15.)

Подставляя это выражение в (11.9.), получим:

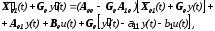
что можно переписать в виде:

(11.16.)

Это дифференциальное уравнение решается относительно переменных 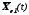, после чего, в соответствии с (11.15.), находятся оцениваемые переменные:

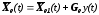.(11.17.)

Сигнал, поступающий на вход объекта,

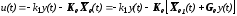, (11.18.)

где матрица коэффициентов разделена на две части

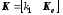, (11.19.)

а 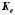имеет размерность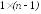. Обобщенная структурная схема замкнутой системы с наблюдением пониженного порядка показана на рис.11.8.

Пример 11.1.

На конкретном примере проиллюстрируем синтез наблюдателя пониженного порядка. Задана система управления двигателем постоянного тока, рассмотренная в примере 10.7.

Уравнения объекта имеют вид:

(11.20.)

Регулятор, синтезированный для этой системы в примере 11.7, обеспечивает выполнение характеристического уравнения:

из которого следует, что замкнутая система имеет постоянную времени 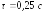и коэффициент затухания. В этом примере синтезируется наблюдатель с постоянной времени; следовательно, этот наблюдатель первого порядка должен иметь характеристическое уравнение

.

Сравнивая уравнения состояния двигателя (11.20.) с уравнениями 11.1., имеем:

,,,

,,.

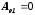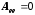По формуле Аккермана (11.13.):

и

.

Тогда на основании (11.16.):

После подстановки матриц и коэффициентов получим уравнение первого порядка:

или

.

Оцениваемое значение получим на основании (11.17.):

. (11.21.)

Уравнением (11.21.) завершена процедура синтеза наблюдателя пониженного порядка, который оценивает угловую скорость двигателя по результату измерения перемещения. Приведенные выше вычисления можно выполнить, используя программы MatLab.

Пример 11.2.

% -------Начало программы Pr_03_10--------

%Расчет одноконтурной системы с наблюдателем

% пониженного порядка.

A=[0,1;0,0];B=[0;1]; %Исходные данные

D=0; %располагаемой системы.

G1=[1,10] %Желаемые параметры

%наблюдателем пониженного порядка.

a11=A(1,1),Ae1=A(2,1),...%Составляющие матрицы коэффициентов,

A1e=A(1,2),Aee=A(2,2) %определяющие параметры наблюдателя

%пониженного порядка.

b1=B(1);Be=B(2); %Составляющие матрицы управления,

%определяющие параметры наблюдателя

%пониженного порядка

G=polyvalm(G1,Aee)*inv(A1e)*1 %Команда, вычисляющая полином

%от матричного аргумента.G1-

%-вектор коэффициентов

%характеристического уравнения.

%Aee-матричный аргумент.

Пример 11.3.

Используя обобщенную структурную схему (рис.10.8) и систему уравнений (11-62-А) определим передаточную функцию наблюдателя. Причем за выходную величину примем координату , а за входную – разность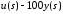

,

Учитывая численные значения коэффициентов () и передаточную функцию наблюдателя, определяем выходной сигнал регулятор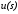а

(11-62-А)

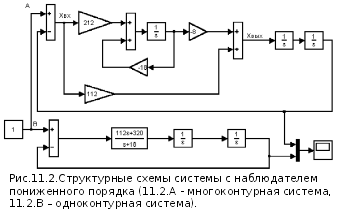
На основании уравнения (11-62-А) на рис.11.2.А представлена детализированная структурная схема исследуемой системы, а на рис.11.2.В структурная одноконтурная схема, полученная из исходной путем эквивалентных преобразований. Уравнение (11-62-А) позволяют определить передаточную функцию регулятора-наблюдателя, как отношение выходного сигнала 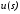к входному сигналу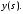

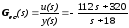. (11.22.)

Так как в выражении (11.22.) 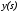- является входом, а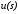– выходом, то систему можно представить в виде структуры с единичной обратной связью, как показано на рис.11.2.В. С учётом передаточных функций регулятораи объектаопределим передаточную функцию разомкнутой системы

и характеристическое уравнение замкнутой системы

,,

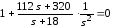. (11.23.)

Сравнение структурных схем рис.11.1 и рис.11.2 позволяет сделать вывод, что матрица коэффициентов, определяющая динамику систем с наблюдателем,- блочная, т.е. характеристические уравнения систем и наблюдателя развязаны. Поэтому коэффициенты матричных обратных связей, которые были определены для заданных динамических характеристик систем, не изменились. Передаточная функция наблюдателя включена последовательно с коэффициентом обратной связи по синтезируемым координатам

.

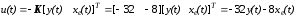Сравнение выражения (11-39) с (11.23.) показывает, что степень полинома числителя характеристического уравнения с наблюдателем пониженного порядка меньше, что положительно сказывается на динамических характеристиках системы.

Пример 11.4.

% -------Начало программы Pr_03_12--------

%Расчет одноконтурной системы с наблюдателем пониженного порядка

A=[0,1;0,0];B=[0;1]; %Исходные данные

D=0; %располагаемой системы.

G1=[1,10] %Желаемые параметры

%наблюдателем пониженного порядка.

a11=A(1,1),Ae1=A(2,1),...%Составляющие матрицы коэффициентов,

A1e=A(1,2),Aee=A(2,2) %определяющие параметры наблюдателя

%пониженного порядка.

b1=B(1);Be=B(2); %Составляющие матрицы управления,

%определяющие параметры наблюдателя

%пониженного порядка

G=polyvalm(G1,Aee)*inv(A1e)*1 %Команда, вычисляющая полином

%от матричного аргумента.

h1=tf([112,360],[1,18]); %Передаточная функция регулятора

h2=tf(1,[1,0,0]) %Передаточная функция объекта.

h=tf(h1*h2/(1+h1*h2)); %Передаточная функция

%замкнутой системы.

step(h,5); %Переходная функция замкнутой системы.

s=dcgain(h) %Коэффициент усиления замкнутой системы.

Комментарии к программе Pr_03_12.После того, как путём структурных эквивалентных преобразований системы с наблюдателями были преобразованы в одноконтурные системы регулирования, для их исследований могут применяться классические методы: определение запасов по фазе и амплитуде, диаграммы Найквиста, ЛАЧ характеристики. В частности, сравнение частотных характеристик систем, представленных на рис.11.5 и рис.11.9, показывают, что применение наблюдателя пониженного порядка увеличивает запас по фазе на 18°и уменьшает перерегулирование. (Для схемы рис.10.5 запас по фазе составляет 38°, а для схемы рис.11.3 запас по фазе составляет 46°).

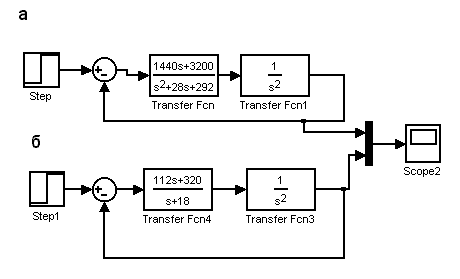
Рис.11.3 Структурные схемы систем с наблюдателями (а-полного порядка, б- пониженного порядка)

Рис.11.4. Переходные характеристики систем регулирования с наблюдателями (1-полного порядка, б – пониженного порядка).

Структурную схему с регуляторов-наблюдателей, расположенным в цепи обратной связи (рис.11.1), можно преобразовать в структурную одноконтурную схему с регуляторов-наблюдателей, расположенным в канале ошибки (рис.11.3). На рис.11.4 представлены результаты моделирования одноконтурных систем. Кривая 1 характеризует систему с регулятором-наблюдателем полного порядка, кривая 2 характеризует систему с регулятором-наблюдателем пониженного порядка. За счет увеличения запаса по фазе система с регулятором-наблюдателем пониженного имеет меньшее перерегулирование.