Синтез линейных непрерывных систем

ЛЕКЦИЯ_10. Расчет непрерывных систем методами современной теории управления

СОДЕРЖАНИЕ

10.1 Определение коэффициентов обратных связей для синтеза систем регулирования

10.2. Определение параметров модальных регуляторов

10.3. Оценка состояния

10.4. Синтез наблюдателя

10.5. Характеристики замкнутой системы

ЭССЕ

По уравнениям пространства состояния или матричным передаточным функциям синтезируются непрерывные системы по заданному расположению корней характеристического уравнения, описан синтез полного и редуцированного наблюдателя. Расчеты иллюстрируются программой MatLab из Simulink и Control System Toolbox. Цель – по заданным требованиям к системам регулирования уметь синтезировать модальные регуляторы и наблюдатели, полный и редуцированный. В пакете Simulink и Control System Toolbox уметь исследовать полученные системы.

Растительное превращение

10.1 Определение коэффициентов обратных связей для синтеза систем регулирования

Классически методы синтеза основаны на использовании передаточных функций, а в современной теории управления модели системы задаются в переменных состояния матричными уравнениями

Уравнения состояния записаны в предположении, что система имеет несколько входных и выходных переменных. Если система характеризуется только одним входом, то матрица имеет вид столбца, а векторпревращается в скалярную переменную. Если у системы только один выход, то векторпревращается в скалярную переменную, а матрицапринимает вид строки. Поэтому, при решении задач в общем виде, будут применены матричные обозначения, а при решении частных (одномерных) задач будут использованы скалярные обозначения.

Предположим, что все выходные координаты объекта поддаются непосредственному измерению и используются в качестве выходного сигнала объекта. Тогда матрица обращается в единичную матрицу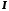, так что. Регулятор осуществляет линейные преобразования выходных сигналов, т.е. алгебраически суммирует сигналы обратных связейс весовыми коэффициентами.

,

где 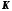- это вектор размерности, характеризующий весовые коэффициенты фазовых координат.

Задача синтеза заключается в том, чтобы поместить корни характеристического уравнения замкнутой системы в заданные точки комплексной плоскости корней путём конструирования матрицы коэффициентов [8].Учитывая, что задание на проектирования системы в виде расположения корней для инженера менее информативно, чем задание переходной или частотной характеристики системы, то в этой части современная теория уступает классической.

Структурная схема замкнутой системы с регулятором в обратных связях представлена на рис.10.1.

Для конструирования матрицы , придающей системе заданные свойства, существует следующая теорема.

Теорема. Задана линейная стационарная располагаемая система с одним входом и одним и одним выходом

и задан - произвольный нормированный многочленn-го порядка, который определяет динамические свойства желаемой системы. Тогда существует вектор обратной связитакой, что замкнутая системаимеетсвоим характеристическим многочленом.

Применение этой теоремы нуждается в комментариях. Исходными данными теоремы являются матрица коэффициентов и матрица управлениярасполагаемой системы. В результате ввода вектора обратных связей получаем характеристическое уравнение синтезируемой замкнутой системы. Таким образом, левые и правые части теоремы имеют разные представления. Поэтому следует или от характеристического уравнения замкнутой системы перейти к матрице коэффициентов желаемой системы, либо от матриц коэффициентовирасполагаемой системы перейти к характеристическому уравнению располагаемой системы.

В литературе освещены оба подхода [ ].Математики обычно задают правую часть в виде матрицы, а инженеры предпочитают использовать передаточные функции и характеристические уравнения желаемой системы. Но, как было показано ранее, переход от характеристического уравнения системы к матрице коэффициентов не однозначен, т.е. одному характеристическому уравнению соответствует множество матриц. Поэтому при решении поставленной задачи матрицы должны быть заданы в одном базисе. Наиболее просто записать матрицув форме УКП (управляемое каноническое представление), так как коэффициенты характеристического уравнения просто связаны с элементами матрицы и, кроме того, фазовые координаты математической модели совпадают с измеряемыми координатами физической модели. Но при записи матрицы желаемой системы в форме УКП необходимо, чтобы и матрицыирасполагаемой системы так же были также записаны в форме УКП, т.е. необходимо согласовать базисы для всех используемых матриц. Нарушения этого условия приводит к ошибкам.

Переходя от характеристического уравнения желаемой системы к матрице коэффициентов , получаем матричную запись теоремы

, (10-1)

где ,- располагаемая и желаемая матрицы системы, записанные в форме УКП.

,(10-2)

где ,-коэффициенты передаточной функции располагаемой и желаемой системы, соответственно.

Приравнивая соответствующие элементы матриц выражения (10-2), получим систему уравнений

( (10-3)

из которых определяются коэффициенты обратных связей (элементы матрицы ).

Пример 10.1.

Пусть задана система:

;.

Эта система полностью управляема, так как .

.

Так как матрицы и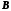представлены не в форме УКП, то нельзя непосредственно воспользоваться теоремой. По матрицеопределим характеристического уравнения располагаемой системы

,

а затем представим матрицы ив форме УКП.

;

Пусть корни желаемого характеристического многочлена замкнутой системы равны:

;;. (10-4)

По характеристическому уравнению (10-4) определяем желаемую матрицу коэффициентов и составляем матричное уравнение (10-1).Тогда компоненты вектора обратной связи определяются из тождества:

Матричное уравнение распадается на два уравнения

Решение этих уравнений дает значение коэффициентов обратной связи

.

Структурная схема скорректированной системы имеет вид (рис.10.2).

Используя теоремы соединения звеньев, получаем передаточную функцию замкнутой системы

.

Так как знаменатель передаточной функции совпадает с характеристическим многочленом замкнутой системы, то вводом коэффициентов обратной связи система получила заданные динамические свойства, что позволяет менять динамику системы, выбирая её характеристические числа (располагая корни на комплексной плоскости) по своему усмотрению.

Решим поставленную задачу, используя характеристическое уравнение замкнутой системы. Так как матрицы можно записать в развернутом виде

.

то имеется возможность определить характеристическое уравнение замкнутой системы через коэффициенты передаточной функции располагаемой системы и компоненты матрицы .

. (10-5)

Приравнивая коэффициенты при одинаковых степенях характеристического уравнения желаемой системы

с уравнением 10-5), получим выражения для определения составляющих вектора

(10-6)

Составляющие вектора , определенные через характеристический многочлен (10-6) и матричные уравнения (10-3), совпадают.

Пример 10.2.

Решим предыдущий пример, если исходные данные представлены в виде передаточной функции

.

Матричная передаточная функция замкнутой системы описывается выражением

,

из которого определяем характеристическое уравнение замкнутой системы

. (10-7)

Так как характеристическое уравнение замкнутой системы не зависит от выбора базиса, то имеется возможность определить компоненты вектора . Приравнивая коэффициенты при одинаковых степеняхвыражения 10-7) с 10-4), получаем

;.

В общем случае на вход системы подаётся векторная величина – матрица . В частном случае – это скаляр. На структурной схеме (рис.10.1) имеется блок, вход которого вектор, а выход скаляр. В этом блоке вектор строка матрицыумножается на вектор столбец фазовых координат, что определяет скалярный выходной сигнал.

Приведенные выше методики, основанные на использования выражения (10-1), требуют представления уравнений системы в одинаковых базисах, например УКП. Если уравнения системы заданы в отличном от УКП базисе, то для определения вектора обратных связей требуется дополнительные преобразования: следует определить матрицу преобразования базисов, перевести уравнения системы в базис УКП, определить в этом базисе вектор обратных связей, а затем полученное решение пересчитать обратно применительно к исходной структуре. Эти преобразования автоматически выполняются в формуле Аккермана [9,10].

, (10-8)

где - матричный полином, образованный путем использования коэффициентов желаемого характеристического уравнения замкнутой системы, т.е.

.

Выражение для матрицы может быть вычислено на компьютере. Проиллюстрируем применение формулы Аккермана следующим примером.