Практическое занятие 2 Исследование термодинамических процессов идеального газа

Рекомендуемая литература

1. Нащокин В.В. Техническая термодинамика и теплопередача. – М.: Высшая школа, 1980. – с. 45-63.

2. Рабинович О.М. Сборник задач по технической термодинамике – М.: Машиностроение, 1969. – с. 57-117.

3. Теплотехника/ М.М. Хазен, Г.А. Матвеев, М.Е. Грицевский, Ф.П.Казакевич/ Под ред. Г.А. Матвеева. – М.: Высшая школа, 1981. –с. 16-39.

4. Юдаев Б.Н. Техническая термодинамика. Теплопередача. – М.: Высшая школа, 1988. – с. 37-56.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Сформулируйте первый закон термодинамики и напишите его аналитическое выражение.

2. От каких параметров состояния зависит внутренняя энергия газов?

3. Чем являются теплота и работа - функцией процесса или состояния? Почему?

4. Что такое энтальпия и энтропия? В чем заключается их физический смысл?

5. Как определить приращение энтропии идеального газа в зависимости от основных термических параметров состояния?

6. Как определить работу и теплоту процесса на - и- диаграммах?

7. В каком случае теплота, работа, изменение внутренней энергии и энтропии считаются положительными? отрицательными?

8. В каком термодинамическом процессе вся теплота идет на совершение работы?

9. В каком термодинамическом процессе работа не совершается?

10. В каком термодинамическом процессе работа совершается за счет изменения внутренней энергии?

11. В каком термодинамическом процессе показатель политропы равен нулю?

Примеры решения задач

Задача 2.1. Воздух массой 10 кг расширяется изотермически при ^оС от начального давления = 800 кПа до конечного объема= 5 м³. Определить начальный объем, конечное давление, работу расширения, теплоту процесса, изменение энтропии, энтальпии и внутренней энергии.

_{Решение. Начальный объем определяем из уравнения состояния для кг газа:}

_м³_.

_{Конечное давление определяем из соотношения параметров в изотермическом процессе:}

_{, (11)}

_{тогда: кПа}

_{Работу расширения в изотермическом процессе определяем по формуле:}

_{. (12)}

_{После подстановки данных имеем:}

_кДж.

_{В изотермическом процессе вся теплота расходуется на совершение работы, поэтому в данном случае кДж.}

_{Изменение энтропии в изотермическом процессе находим по формуле:}

_{, (13)}

_{тогда кДж/кг·К.}

_{Энтальпия и внутренняя энергия идеального газа в изотермическом процессе не изменяются, таким образом, и .}

_{Ответ: м}³_{; кПа; кДж;}

_{кДж/кг·К; и .}

_{Задача 2.2. Сухой воздух массой 1 кг совершает прямой термодинамический цикл, состоящий из четырех последовательных термодинамических процессов.}

_{Заданные параметры для воздуха: МПа, 300 К, МПа, = 273 К. Процессы: 1-2 -} ; 2-3_-; 3-4 -; 4-1 -.

_{Требуется:}

_{1. Рассчитать давление Р, удельный объем v, температуру воздуха Т для основных точек цикла.}

_{2. Для каждого из процессов определить значения показателей политропы n, теплоемкости c, вычислить изменение внутренней энергии , энтальпии , энтропии , теплоту процесса q, работу процесса , располагаемую работу .}

_{3. Определить суммарные количества подведенной q1 и отведенной q2 теплоты, работу цикла ц, термический КПД цикла t.}

_{4. Построить цикл в vP - и sT - координатах.}

_{Принять газовую постоянную 287,3 Дж/(кгК), теплоемкость при постоянном давлении =1,025 кДж/(кгК), что соответствует свойствам сухого воздуха при Т=273 К.}

Решение.

1. Определим параметры в характерных точках.

_{Точка 1. К.}

_{Точка 2. Процесс 1-2 – адиабатный}

_{Показатель адиабаты:;}

_{кДж/(кгК)}

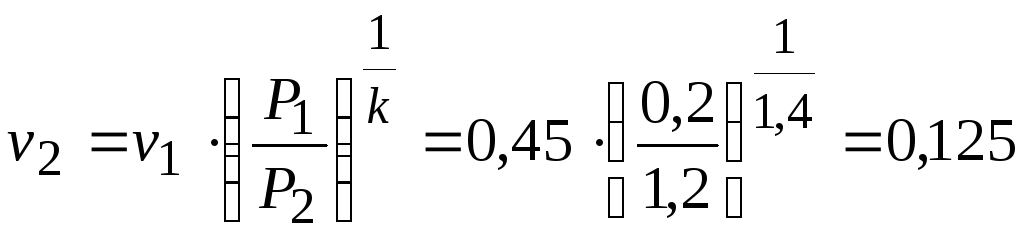_м³_{/кг. 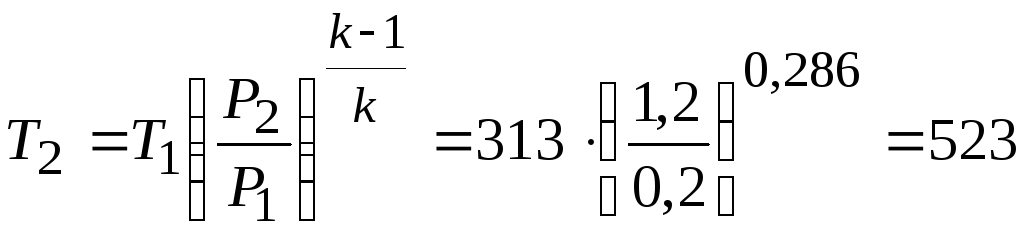К.}

_{Точка 3. Процесс 2-3 – изохорный => =0,125 м}³_/кг.

_МПа.

_{Точка 4. м}³_/кг.

_К

_{Таблица 2.1.}

_{Результаты вычислений}

Термические параметры	Точка цикла
	1	2	3	4
Р, МПа	0,2	1,2	1,3	0,2
v, м3/кг	0,45	0,125	0,125	0,5
Т, К	313	523	573	335

_{2. Рассчитаем параметры процессов.}

_{Процесс 1-2 – адиабатный:} .

Показатель политропы рассчитаем по формуле:

. (14)

Для данного процесса: .

Теплоемкость:

. (15)

В адиабатном процессе теплоемкость равна нулю, т.к. :

.

_{Изохорная теплоемкость: кДж/кг·К}

Изменение внутренней энергии и энтальпии:

кДж/кг;

=215,25 кДж/кг.

_{Изменение энтропии определяется по формуле:}

_{. (16)}

_{Т.к. в адиабатном процессе , то и} =0.

В адиабатном процессе работа совершается за счет изменения внутренней энергии:

=-, (17)

тогда: =-=-154,98 кДж/кг.

_{Располагаемая работа в адиабатном процессе в раз больше работы изменения объема:} = =1,4·кДж/кг.

_{Процесс 2-3 – изохорный: .}

_{В изохорном процессе показатель политропы равен бесконечности:}

.

= 0,738 кДж/(кг·К).

Изменение внутренней энергии и энтальпии:

кДж/кг;

кДж/кг.

Изменение энтропии в изохорном процессе определяется по формуле:

, (18)

Тогда в данном случае: кДж/кг·К.

В изохорном процессе вся теплота расходуется на изменение внутренней энергии: 36,9 кДж/кг.

Работа в изохорном процессе равна нулю за счет того объем остается постоянным: .

Располагаемая работа: кДж/кг

_{Процесс 3-4 - адиабатный:} .

; =0.

кДж/кг;

=-243,95 кДж/кг;

=-=175,6кДж/кг;==1,4·кДж/кг;=0

_{Процесс 4-1 – изобарный:} , т.е..

Таким образом,

Теплоемкость процесса: кДж/(кг·К).

кДж/кг;

кДж/кг;

=кДж/(кг·К);

=-22,55 кДж/кг;

кДж/кг; .

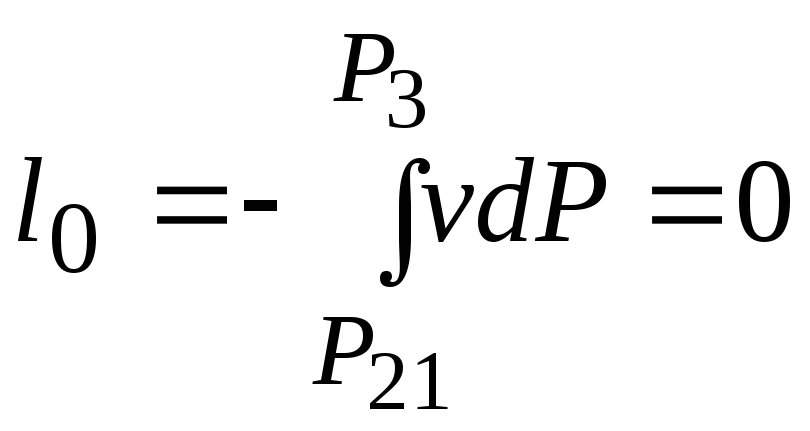3. _{Определим суммарные количества подведенной q1 и отведенной q2 теплоты, работу цикла , термический КПД цикла t.}

Подведенная теплота: кДж/кг.

Отведенная теплота: кДж/кг.

Работа цикла:=36,9-22,55=14,35 кДж/кг.

Термический КПД цикла :

4. Для построения цикла в координатах необходимо определить значение энтропии(Дж/кг∙К) для каждой характерной точки цикла по формуле:

_{. (19)}

_{Далее получаем:}

_{кДж/(кг·К);}

_{кДж/(кг·К);}

_{кДж/(кг·К);}

_{кДж/(кг·К).}

_{Вычислим значения изменения энтропии в термодинамическом цикле:}

_{кДж/(кг·К);}

_{кДж/(кг·К);}

_{кДж/(кг·К);}

_{кДж/(кг·К).}

_{Вычисленные значения изменения энтропии совпадают со значениями, полученными для процессов цикла через основные термодинамические параметры.}

_{Таблица 2}

_{Результаты вычислений энтропии в точках цикла}

	Точка 1	Точка 2	Точка 3	Точка 4
, К	313	523	573	335
, кДж/(кг·К)	- 0,06	- 0,06	0,01	0,01

Цикл в - координатах строим, используя результаты вычислений п.1 (таблица 2.1.):

_{Рис. 2. Цикл в vP-координатах}

_{Рис. 3. Цикл в sT – диаграмме}

задачи для самостоятельного решения

Задача 2.3. Какое количество теплоты необходимо подвести к воздуху в закрытом сосуде объемом м³, если начальная температура _{t1 =100} ^о_{С , давление = 300 кПа, а конечная температура t2 =500} ^о_{С? Определить также массу воздуха и конечное давление. Зависимость теплоемкости от температуры считать нелинейной.}

Ответ: = 1,4 кг;= 412 кДж;= 623 кПа.

Задача 2.4. _{В изохорном процессе температура окиси углерода массой m = 2,1 кг с начальным давлением p1 = 0,12 МПа изменяется от t1= 25}^о_{С до t2=63}^о_{С. Определить параметры состояния рабочего тела в точках 1 и 2, а также теплоту, энтальпию и изменение внутреней энергии 1 кг окиси углерода в процессе. Принять ср = 1,0464} кДж/кг∙К, =296,8 кДж/кг∙К. Изобразить процесс в _{vр- и sT-диаграммах.}

Ответ: К;м³/кг; _К; 0,735 м³/кг; _;;кДж/кг.

Задача 2.5_{. Воздух массой m = 1,9 кг с начальным давлением p1 =0,22 МПа адиабатно расширяется. При этом его температура изменяется от t1 =65} ^о_{С до t2 =21}^о_{С. Определить параметры состояния рабочего тела в точках 1 и 2, а также теплоту, энтальпию и изменение внутреней энергии 1 кг азота в процессе. Принять ср = 1,0121} кДж/кг∙К, =287 кДж/кг∙К.

_{Представить процесс в vр- и sT-диаграммах.}

Ответ: _К; м³/кг; _К; 0,54 м³/кг; _;;кДж/кг;= - 44,53 кДж/кг.