4.1.5. Определим изменение метацентрической высоты судна при заливании промысловой палубы слоем воды 0,3 м.

Метацентрическая высота меняется, во-первых, вследствие приёма груза и, во-вторых, из-за наличия свободной поверхности. Воспользуемся формулой начальной остойчивости:

где i_x – момент инерции площади свободной поверхности воды относительно оси наклонения.

М = 4573,5 (т);

М_х = - 14684,7 (т·м);

d_H = 4,1 (м);

d_К = 5,78 (м);

d = 4,94 (м);

Х_с = - 3,21 (м);

L_П.П. = 96,4 (м) – длина судна между перпендикулярами;

l_{пром. палубы} = 43 (м) – длина промысловой палубы;

b_{пром. палубы} = 8,6 (м) – ширина промысловой палубы;

h_в = 0,3 (м); -высота воды над промысловой палубой;

ρ = 1,025 – плотность морской воды;

Найдём неизвестные элементы входящие в состав формулы:

(м³);

(т);

i_x = k · l · b³ = (м⁴), где - коэффициент учитывающий форму резервуара со свободной поверхностью.

М₁ = М + m = 4573,5 + 113,7 = 4687,2 (т);

По диаграмме посадок БАТМ “Пулковский Меридиан” (приложение 2.2) снимем новые осадки носом и кормой:

d_К1 = 5,89 (м) и d_H1 = 4,13 (м) => d₁ = 5,01 (м);

= d₁ – d = 5,01 – 4,94 = 0,07 (м);

(м);

4.1.6. Определим уменьшение метацентрической высоты от обледенения, если период бортовой качки увеличился на 20%.

Для решения данной задачи будем пользоваться формулой для периода бортовой качки , полагая, что инерционный коэффициент С до и после обледенения сохраняет своё значение.

В = 16 (м) – ширина судна;

=> =>(м);

δh = h₁ – h = 0,57 – 0,82 = - 0,25 (м);

4.1.7. Определяем угол крена судна на установившейся циркуляции при скорости судна на прямом курсе 12 узлов.

Наибольший кренящий момент на циркуляции находим по формуле:

где V – скорость судна на прямом курсе.

М = 4573,5 (т);

d = 4,94 (м);

Z_g = 6,92 (м);

L_П.П. = 96,4 (м);

g = 9,81 (м/с²);

h = 0,82 (м);

(Н·м);

Угол крена на циркуляции будет равен:

4.1.8. Определяем метацентрическую высоту судна, сидящего на мели без крена с осадкой носом и кормой на 0,5 м меньше, чем на глубокой воде. Определяем критическую осадку, при которой судно начинает терять устойчивость.

Восстанавливающий момент судна, сидящего на мели, подсчитываем по формуле:

где V и V_a – объёмное водоизмещение судна до и после посадки на мель; Δa = γ ·V_a – вес вытесненной воды после посадки на мель; Δ = γ ·V – вес судна; Z_ma – аппликата поперечного метацентра судна, сидящего на мели.

М = 4573,5 (т);

d_H = 4,1 (м);

d_К = 5,78 (м);

d = 4,94 (м);

Z_g = 6,92 (м);

(м³);

Находим вес судна до посадки на мель:

Δ = γ ·V = ρ · g · V = 1,025 · 9,81· 4461,95 = 44866,0 (кН);

Из формулы для М_В видно, что метацентрическая высота судна, сидящего на мели равна:

Z_ma и Δa находим по диаграмме посадок (приложение 2.2) и кривым Z_c(d_H, d_К) и r(d_H, d_К) (приложения 2.3 и 2.4).

После посадки судна на мель:

d_Ha = 3,6 (м) и d_Кa = 5,28 (м) => da = 4,44 (м) => Мa = 3900 (т);

(м³);

Находим вес судна после посадки на мель:

Δа = γ ·V_а = ρ · g · V_a = 1,025 · 9,81· 3804,9 = 38259,2 (кН);

Находим Z_ma как сумму Z_са и r_а, найденных из приложений 2.3 и 2.4:

Z_са = 2,53 (м) и r_а = 5,07 (м) => Z_ma = Z_са + r_а = 2,53 + 5,07 = 7,60 (м);

Из формулы для М_В видно, что метацентрическая высота судна, сидящего на мели равна: (м);

Для определения критической осадки сводим данные в таблицу и на её основе строим график зависимости V_a· Z_ma от осадки d.

Критическую осадку d_кр определяем графическим способом при V_a· Z_ma = V· Z_g;

Таблица 5.

d	dH	dК	Ma		Zса	ra	Zma = Zса + rа	Va· Zma
4,94	4,10	5,78	4573,50	4461,95	2,88	4,86	7,74	34535,49
4,44	3,60	5,28	3900,00	3804,90	2,53	5,07	7,60	28917,24

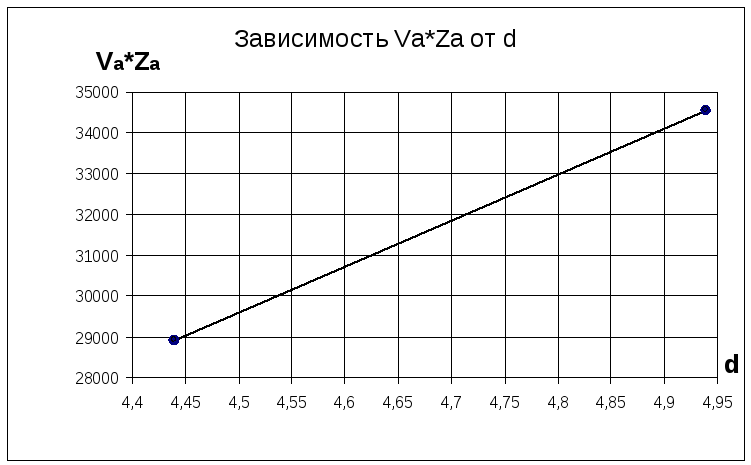
V· Z_g = 4461,95 · 6,92 = 30876,7;

Так как V· Z_g для данного варианта загрузки равно 30759,9, то согласно графику находим, что критическая осадка, при которой судно начинает терять устойчивость составляет d_KP = 4,57 (м).

4.1.9. Определяем динамические углы крена от динамически приложенного кренящего момента, от давления ветра для двух случаев положения судна. В первом случае наклонения происходят с прямого положения, во втором – судно накренено на наветренный борт на угол, равный амплитуде бортовой качки.

Динамически приложенный кренящий момент М_КР подсчитываем по формуле: М_КР = 0,001· р · S· z

где р – давление ветра;

S – площадь парусности;

z – отстояние центра парусности от плоскости действующей ватерлинии;

Давление ветра р принимают в зависимости от района плавания и плеча парусности z. Площадь парусности S и плечо парусности z снимаются с графиков в приложении 2.9 в зависимости от средней осадки:

z = 6,15 (м) и S = 1100 (м²) => р = 1175,7 (Н/м²);

М_КР = 0,001· 1175,7 · 1100 · 6,15 = 7953,6 (кН·м);

Площадь скуловых килей БАТМ “Пулковский Меридиан” равна: 2 х 14,2 м²;

Амплитуда качки вычисляется по формуле :;

где х₁ и х₂ – безразмерные множители, зависящие соответственно от отношения В/d и коэффициента общей полноты δ; Y – множитель (град.); k – коэффициент, зависящий от отношения суммарной площади скуловых килей к произведению L·B.

Значения х₁, х₂, k выбираются из таблиц на стр. 24-25 методички в зависимости от отношения В/d, коэффициента общей полноты δ и отношения скуловых килей А_к к произведению L·B.

В/d = 16/4,94 = 3,24 => х₁ = 0,86;

=> х₂ = 0,95;

=> k = 0,9;

Y вычисляем в зависимости от отношения :

=> Y = 27,0;

Окончательно получаем: Θ_m = 0,9 · 0,86 · 0,95 · 27 = 19,9⁰;

Плечо кренящего момента вычисляем следующим образом:

(м);

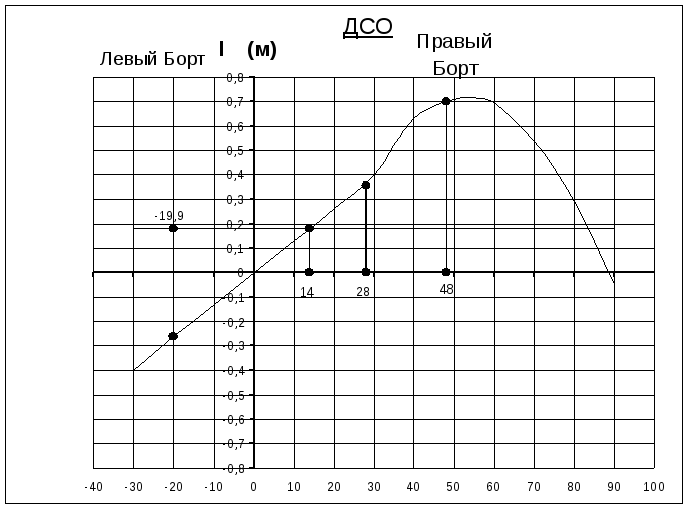
Динамические углы крена Θ_д при действии на судно момента М_КР находим из условия равенства работ восстанавливающего и кренящего моментов при наклонении судна в первом случае от 0⁰ до Θ_д, во втором – от -Θ_m до Θ_д. Работы восстанавливающего и кренящего моментов при наклонении геометрически представляются площадями, ограниченными соответственно диаграммой статической остойчивости и кривой плеч кренящего момента, а также осью абсцисс и ординатами 0⁰ и Θ_д в первом случае и -Θ_m и Θ_д – во втором.

На ДСО откладываем плечо кренящего момента в виде прямой .

Для первого случая при наклонении судна от 0⁰ до Θ_д равенство работ восстанавливающего и кренящего моментов выражается равенством площадей 1-2-3 и 3-4-5.

Получается Θ_д1 = 28⁰.

Для второго случая при наклонении судна от -Θ_m = - 18,7⁰ до Θ_д равенством работ восстанавливающего и кренящего моментов выражается равенством площадей 1^’-2’-3 и 3-4’-5’.

Получается: Θ_д2 = 45⁰.