1.7 Примеры выполнения ргр.

Пример 1.Исследовать функцию и построить график.

1. Область определения функции ;

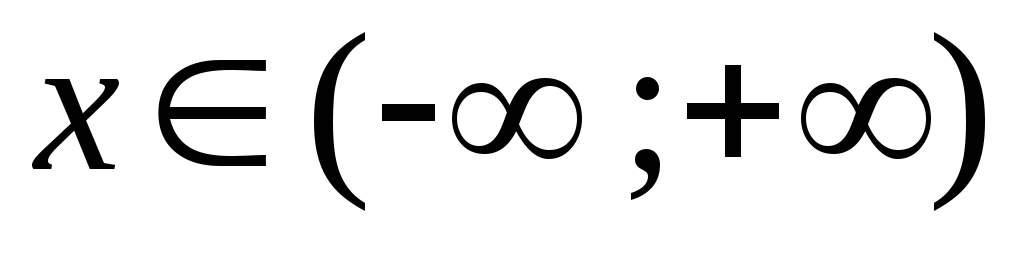2. Исследуем функцию на четность и нечетность: 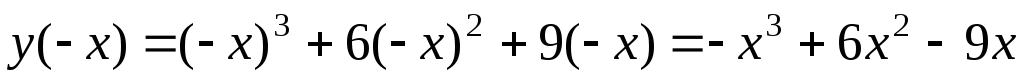. Получил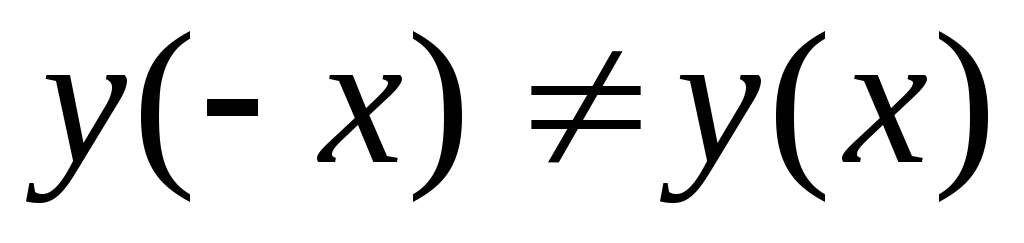и,и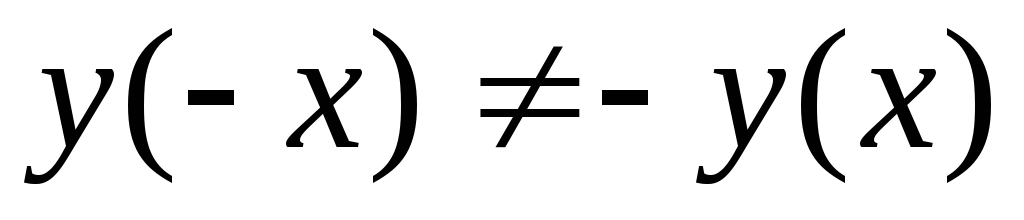, т.е. данная функция общего вида.

3. Находим точки пересечения с осями координат:

при ,

при решаем уравнение

Точки пересечения (0; 0) и (-3; 0).

4. Найдем интервалы возрастания и убывания функции, экстремумы. Для этого найдем производную и решим уравнение.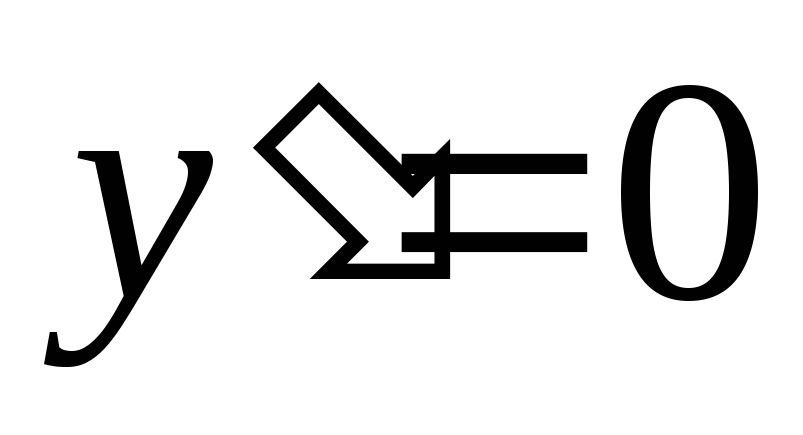

Производная обращается в ноль при или.

Критические точки

Для проверки достаточных условий экстремума и определения интервалов убывания, возрастания составим таблицу. Полезно нанести критические точки на числовую ось.

	+	0		0	+
	Возрастает	0 max	Убывает	-4 min	Возрастает

Производная сохраняет знак в каждом из указанных интервалов. Для его определения выберем в каждом интервале пробную точку и определим знак производной в этой точке. Например, в первом интервале выберем точку. Вычислим

, производная больше нуля, функция на этом интервале возрастает и т.д. При переходе через точку производная меняет знак с «плюса» на «минус», следовательно, точка (-3; 0) точка максимума; (-1;-4) - точка минимума.

5. Найдем точки перегиба графика функции. Для этого определим вторую производную и решим уравнение.

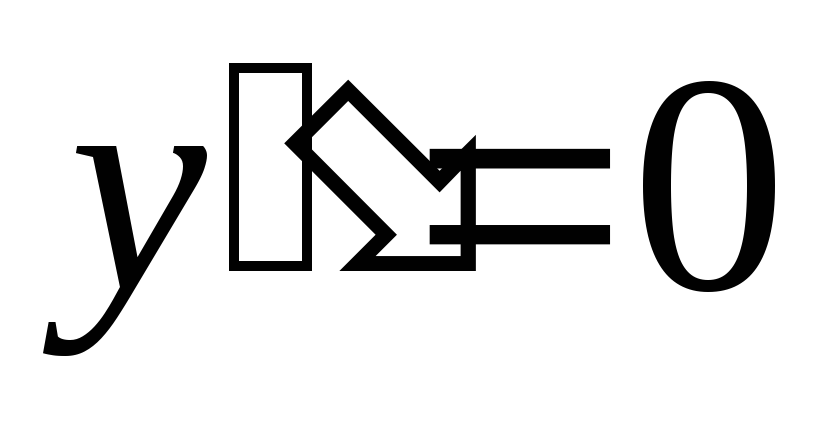- критическая точка. Для проверки достаточных условий выпуклости, вогнутости составим таблицу.

		0	+
	Выпуклая	-2 Точка перегиба	Вогнутая

На интервале вторая производная имеет отрицательный знак – график функции на этом интервале выпуклый, на интервалевторая производная положительная – график функции на этом интервале вогнутый, точка (-2; -2) - точка перегиба.

6. Строим график функции (рис. 7). Находим дополнительные точки

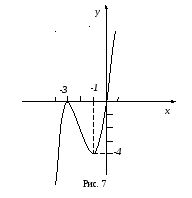
Пример 2. Исследовать функцию и построить график.

1. Область определения 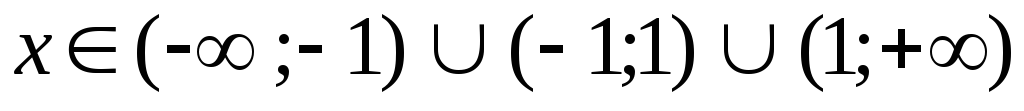, т.е..

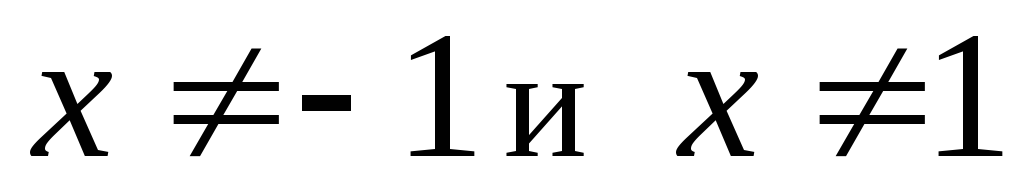2. Функция нечетная .

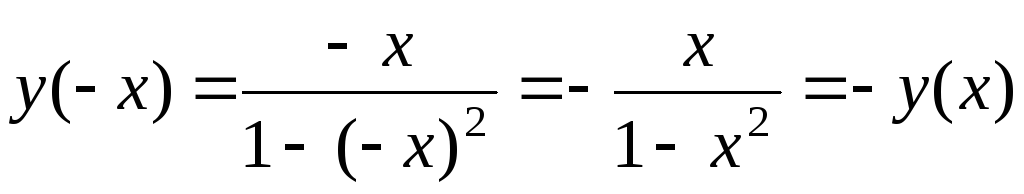3. Точка пересечения с осями (0; 0).

4. Интервалы знакопостоянства. Разложим знаменатель на множители 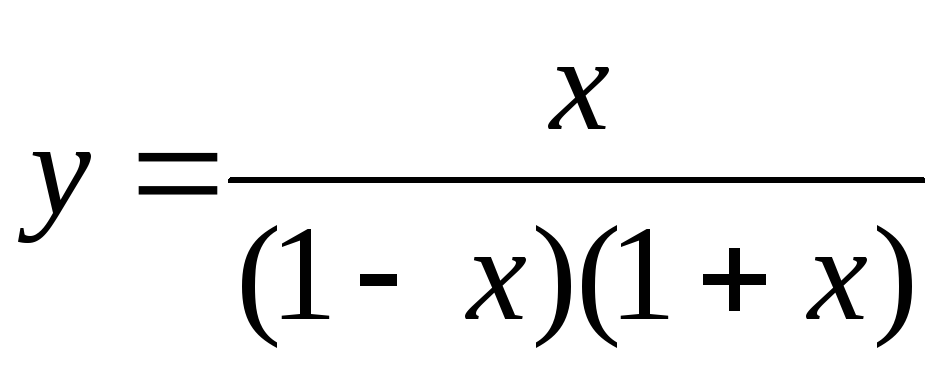. На числовой прямой изобразим точки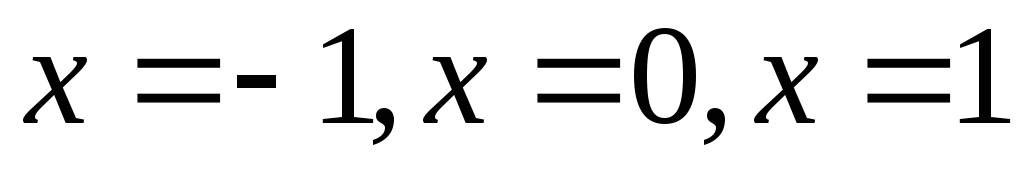и определим знак функции в каждом из полученных интервалов.

На интервалах ифункция имеет положительный знак, на интервалахи- отрицательный.

5. Находим асимптоты. Точки с абсциссами 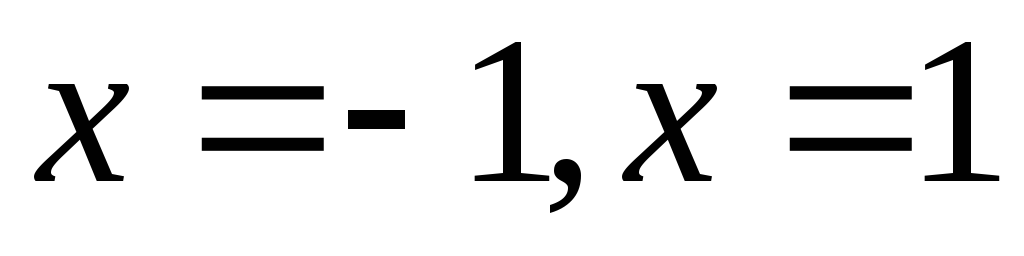являются точками разрыва, следовательно, вертикальные асимптоты прямые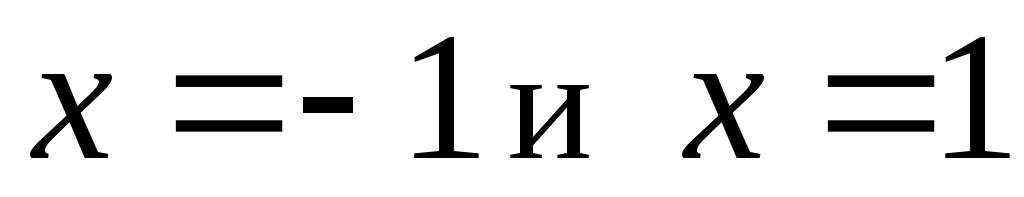. Определим односторонние пределы в этих точках.

Наклонную асимптоту будем искать в виде .

Получили: - горизонтальная асимптота.

6. Находим интервалы убывания, возрастания, экстремумы функции. Для этого найдем производную и решим уравнение.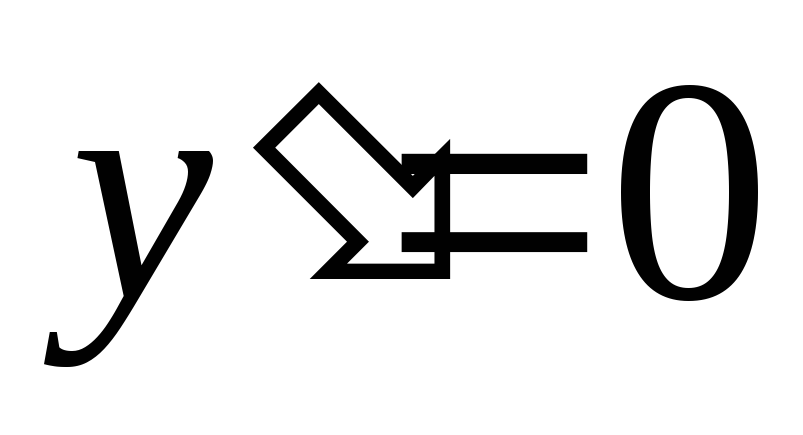

Производная не обращается в нуль ни в одной точке. В точках производная не существует, но эти точки не принадлежат области определения, поэтому точек экстремума нет. На числовой прямой изображаем точкии определяем интервалы убывания и возрастания функции.

В каждом из интервалов производная имеет положительный знак, следовательно функция возрастает на всей области определения.

7. Определяем точки перегиба, интервалы выпуклости и вогнутости. Находим вторую производную и решаем уравнение .

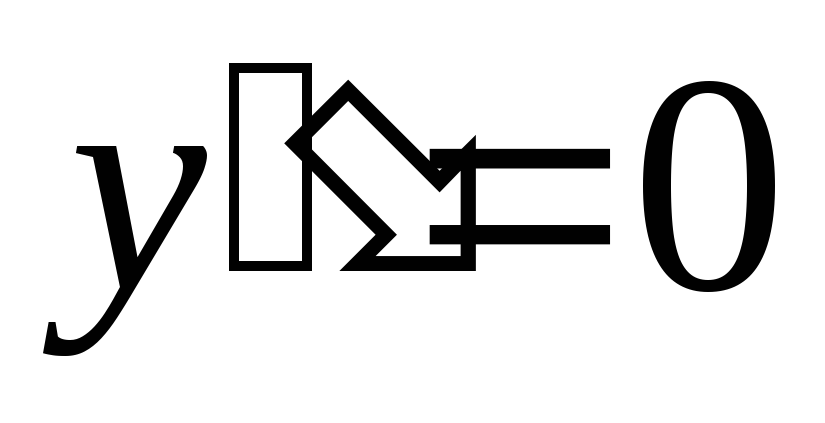Критические точки . Для проверки достаточных условий выпуклости, вогнутости составляем таблицу.

	+		0	+	─
	Вогнутая	Выпуклая	0 Точка перегиба	Вогнутая	Выпуклая

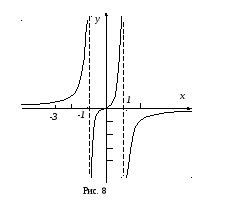
8. Строим график функции (рис. 8).

Дополнительные точки .