19

МИНИСТЕРСТВО АГРАРНОЙ ПОЛИТИКИ И ПРОДОВОЛЬСТВИЯ УКРАИНЫ

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РЫБНОГО ХОЗЯЙСТВА УКРАИНЫ

Керченский государственный морской технологический университет

Кафедра высшей математики и физики

ВЫСШАЯ МАТЕМАТИКА

Методические указания

по выполнению расчетно-графической работы раздела высшей математики

«Математический анализ»

( исследование функций и построение графиков, построение эмпирической формулы методом наименьших квадратов)

для студентов дневной формы обучения

специальности «Эксплуатация судовых энергетических установок»

направления 6.070104 «Морской и речной транспорт»

Керчь, 2009

Автор: Драчева И.А., ассистент кафедры высшей математики и физики КГМТУ

Рецензент: Моисеенко С.С., ст. преподаватель кафедры высшей математики и физики КГМТУ

Методические указания рассмотрены и одобрены на заседании кафедры высшей математики и физики КГМТУ,

протокол № от 2009 г.

Методические указания рассмотрены и рекомендованы к утверждению на заседании методической комиссии технологического факультета КГМТУ

протокол № от 2009 г.

Методические указания утверждены на заседании методического совета КГМТУ,

протокол №___ от _________2009 г.

© Керченский государственный морской технологический университет, 2009

Содержание

	Введение………………………………………………………………………	4
1	Исследование функций и построение графиков……………………………	5
1.1	Определение функции. Основные характеристики………………………..	5
1.2	Признаки монотонности функции………………………………………….	6
1.3	Экстремумы функции………………………………………………………..	6
1.4	Выпуклость вогнутость. Точки перегиба……………………………………	7
1.5	Асимптоты…………………………………………………………………….	8
1.6	Общая схема исследования и построение графиков функции……………..	9
1.7	Примеры выполнения РГР……………………………………………………	10
2	Понятие об эмпирических формулах. Метод наименьших квадратов……	14
2.1	Эмпирические формулы……………………………………………………...	14
2.2	Определение параметров линейной зависимости методом наименьших квадратов………………………………………………………………………	15
2.3	Пример выполнения РГР……………………………………………………..	16
	Рекомендуемая литература…………………………………………………..	18

Введение

Расчетно-графическая работа для студентов 1-го курса (I семестр 2-я четверть) специальности «Судовые энергетические установки» выполняется по следующим разделам математического анализа:

- приложение производной, исследование функций и построение графиков;

- функции нескольких переменных, построение эмпирической формулы методом наименьших квадратов.

В первом задании надо с помощью производной исследовать функции и поострить их графики, во втором задании методом наименьших квадратов составить эмпирическую формулу, выражающую зависимость между двумя величинами х иy .

В данных методических указаниях в краткой форме изложен теоретический материал по данным темам, разбираются решения подобных задач РГР. Методические указания должны помочь студентам в самостоятельном выполнении расчетно-графической работы, а также в подготовке к модульному и семестровому контролю.

Задания по РГР выдаются преподавателем, ведущим практические занятия по высшей математике. Расчетно-графическая работа должна быть выполнена студентом в отдельной тетради и сдана преподавателю на проверку. Работа выполняется аккуратно с подробным объяснением решения задачи. Студент должен защитить свою работу, решив подобную задачу или ответив на вопросы преподавателя по РГР.

Методические указания могут использоваться студентами других специальностей, как морского факультета, так и технологического.

1. Исследование функций и построение графиков.

1. Определение функции. Основные характеристики функций.

Если каждому значению переменной х из множестваХпо некоторому правилу поставлено в соответствие единственное вполне определенное значениеy,то переменнуюyназываютфункциейотх. Записываютили . Говорят ещё, что функция отображает множествоХна множествоY .

Множество Хназывается областью определения функции и обозначается. Множество всехназывается множеством значений функции и обозначается.х – независимая переменная величина или аргумент,y – функция или зависимая переменная.

Функция , определенная на множественазываетсячетной, если для любоговыполняется условиеи;нечетной,если для любоговыполняется условиеи.

График четной функции симметричен относительно оси Оy, нечетной – относительно начала координат.

Например: - четные функции; а- нечетные функции;- функции общего вида, т.е. не четные и не нечетные.

Функция называетсяпериодическойна множествеD, если существует такое числоТ>0, что при каждом значениии. При этом числоТназываетсяпериодом функции.

Функция называетсявозрастающейв интервале, если для любых двух точекииз указанного интервала, удовлетворяющих неравенству, выполняется неравенство, если, функция называетсянеубывающей.

Иными словами – значения возрастающей функции увеличиваются одновременно со значением аргумента.

Функция называетсяубывающей в интервале, если для любых двух точекииз указанного интервала, удовлетворяющих неравенству, выполняется неравенство, если, функция называетсяневозрастающей.

Возрастающие, невозрастающие, убывающие и неубывающие функции называются монотонными. А возрастающие и убывающие –строго монотонными.

Функция, заданная графиком на рис. 1, убывает на интервале (-2; 1), не убывает на интервале (1; 3), возрастает на интервале (3; 5).

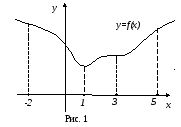
2. Признаки монотонности функции.

1. Если функция дифференцируема на интервале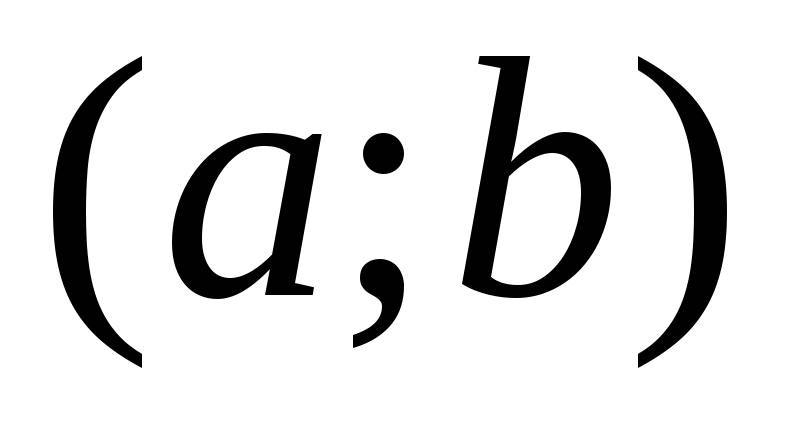иво всех точках интервала, то функциявозрастает на этом интервале.

2. Если функция дифференцируема на интервалеиво всех точках интервала, то функция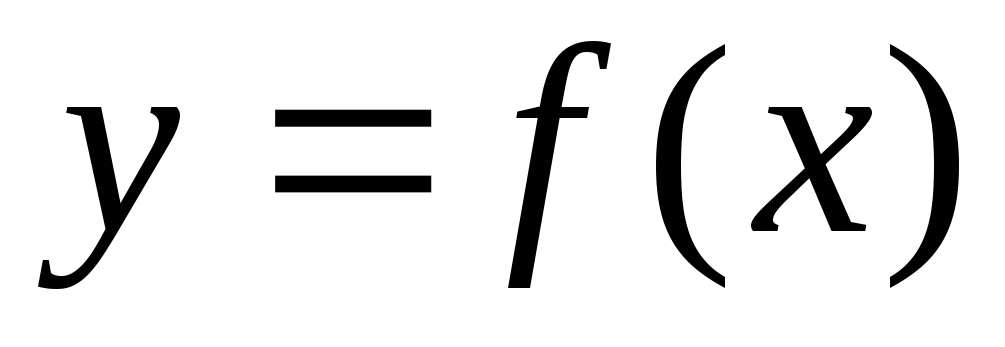убывает на этом интервале.

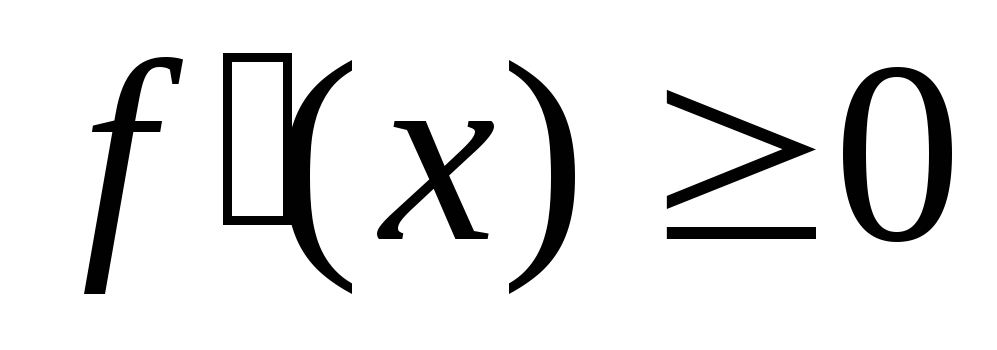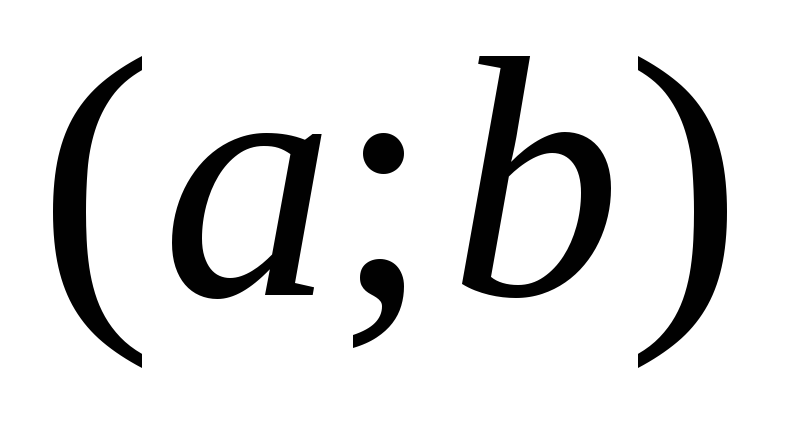3. Если () для всех точек интервала, то функция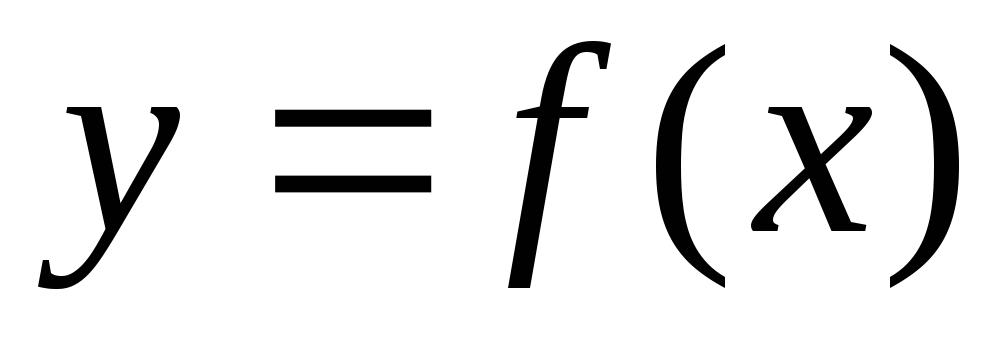не убывает (соответственно, не возрастает) на этом интервале, т.е. для любых двух точек из интервала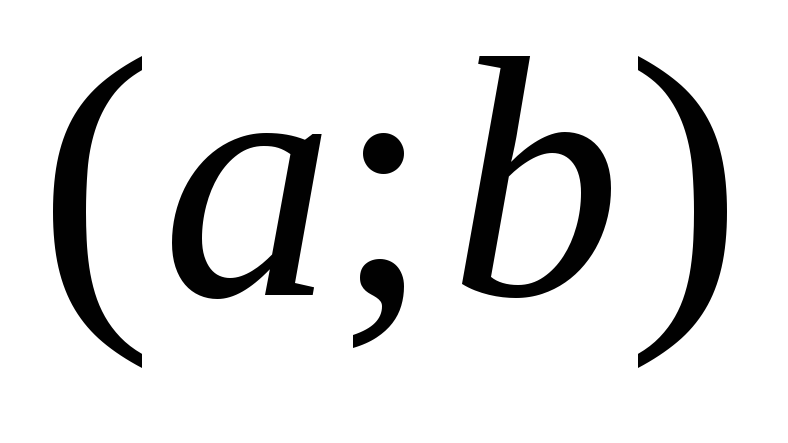из неравенстваследует(соответственно,).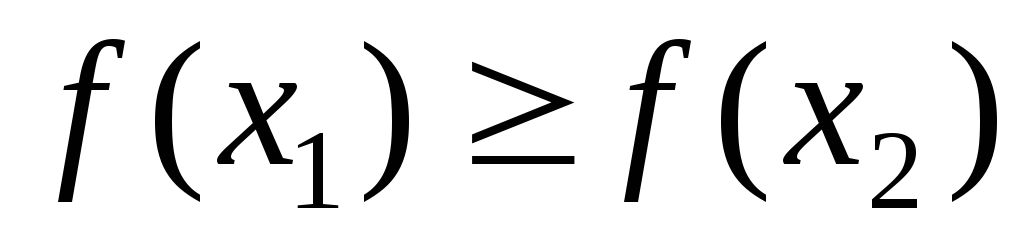

1.3 Экстремумы функции.

Точка называетсяточкой максимумафункции, если значениеявляется наибольшим в некоторой окрестности этой точки.

Точка называетсяточкой минимумафункции, если значениеявляется наименьшим в некоторой окрестности этой точки.

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках –экстремумами функции (рис. 2).

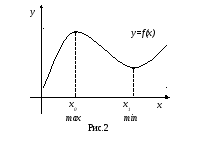
Теорема (Ферма – необходимое условие экстремума).Если- точка экстремума для функции, то в этой точке производная функции либо равна нулю, либо не существует.

Точки области определения функции , в которых ее производная не существует или равна нулю, называютсякритическими точкамифункции.

В силу теоремы Ферма экстремумы функции находятся среди ее критических точек.

Первое достаточное условие экстремума. Если при переходе (слева направо) через критическую точкупроизводнаяменяет знак с (+) на (-), то точкаявляется точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет.

Второе достаточное условие экстремума. Пусть в точкепроизводная равна нулю, а вторая производная. Тогда, если, то- точка минимума; если, то- точка максимума.