4.5Векторное произведение векторов

4.5.1 Рассмотрим трехмерное евклидово пространство Е³;

(i, j, k) - ортонормированный базис в этом пространстве.

Векторным произведением векторов называют такой вектор , что

1)

то есть длина вектора равна площади параллелограмма, построенного на этих векторах;

2) вектор перпендикулярен плоскости, в которой лежат векторы ;

3) векторы образуют правую - тройку, то есть вектор направлен так, что, если смотреть с конца вектора , то кратчайший поворот от совершается против часовой стрелки.

Векторное произведение обозначается или .

Свойства векторного произведения:

1.

2. , λ - скаляр;

3.

Пример 19. Найти векторное произведение ортов (базисных векторов) i, j, k.

Решение

, так как

аналогично ;

Согласно определению:

4.5.2 Векторное произведение в координатной форме.

Пусть известны координаты векторов , то есть

Используя свойства векторного произведения, найдем:

Выражения в скобках можно записать с помощью определителей второго порядка (проверьте), то есть:

правую часть последнего выражения можно записать с помощью определителя третьего порядка:

Эта формула является удобной записью векторного произведения в координатах.

Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Из определения векторного произведения следует, что площадь параллелограмма, построенного на векторах , равна модулю векторного произведения:

в частности, площадь треугольника

Одним из физических приложений векторного произведения является нахождение момента силы, возникающего при вращении твердого тела, закрепленного в некоторой точке А, под действием силы , приложенной в точке В:

Пример 20. Найти площадь треугольника АВС, где А (-2, 1, 0);

В (3,4, 8); С (-1,3,6).

Решение

Площадь треугольника, построенного на векторах и , равна

Найдем координаты векторов:

=(-1+2; 3-1; б-0)=(1,2,6)

=(3-(-2); 4-1; 8-0)=(5, 3, 8)

их векторное произведение равно:

Итак, или

4.6 Смешанное произведение векторов

При последовательном умножении трех векторов возможны следующие случаи:

1) где λ - скаляр,

2) - двойное векторное произведение, в результате получим вектор;

3) - векторно-скалярное произведение, в результате получим число.

Смешанным произведением трех векторов называется их векторно-скалярное произведение, обозначают:

Найдем выражение смешанного произведения через координаты.

Пусть тогда векторное произведение в координатах записывается в виде:

тогда скалярное произведение в координатах имеет вид:

Правую часть последнего выражения можно записать с помощью определителя третьего порядка. Итак, смешанное произведение в координатах имеет следующий вид:

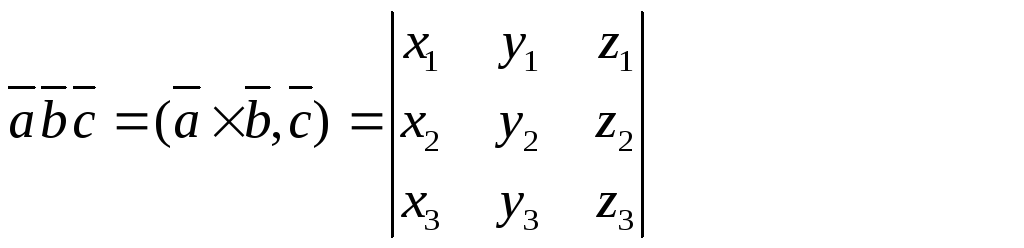
Свойства смешанного произведения векторов (проверьте самостоятельно):

1)

2)

3) Пусть - некомпланарные векторы.

Построим на этих векторах параллелепипед.

Смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на этих векторах.

Действительно, то есть , где S_ABCD - площадь основания.

Скалярное произведение Очевидно, что , где H высота параллелепипеда.

Итак,

или, так как

В частности, объем пирамиды, построенной на векторах равен

4) Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

- компланарные

Пример 21. Показать, что заданные четыре точки лежат в одной

плоскости: А(2, 0, 1); В(-3, 1, 0); С(0,1, 3); D(-4, 3, 7).

Решение.

Заданные точки лежат в одной плоскости, если три вектора также лежат в этой плоскости, то есть, если эти векторы компланарны.

Векторы компланарны, если их смешанное произведение равно нулю.

Найдем координаты векторов:

тогда смешанное произведение равно

то есть заданные точки лежат в одной плоскости.

Пример 22. Найти объем пирамиды ABCD, где А(2, 0, 1); В(3, -1, 4);

C(0,-5,1); D(0,0,4).

Решение

Объем пирамиды равен

Найдем координаты векторов

тогда смешанное произведение:

Следовательно, объем пирамиды