4.3.3 Теорема о разложении вектора по базису

Всякий элемент n-мерного линейного пространства можно представить, притом единственным образом, как линейную комбинацию векторов базиса.

Доказательство. Пусть ē₁, ē₂, …, ē_n - базис линейного пространства L. Рассмотрим любой вектор ā L. Тогда система векторов ē₁,…, ē_n, ā - линейно зависимая, то есть λ₁ē₁+…+ λ_nē_n+ λ_n+1 ā=0 , причем λ_n+1≠0.

Если λ_n+1=0, тогда и какое-то из λ_i≠0

Это означает: ē₁, ē₂, …, ē_n - линейно зависимы, что противоречит условию: ē₁, ē₂, …, ē_n - базис, то есть линейно независимая система векторов.

Итак, λ_n+1≠0, тогда, то есть

, где .

Таким образом, показали, что любой вектор можно представить как линейную комбинацию векторов базиса.

Покажем, что такое разложение единственно. Предположим, что наряду с полученным разложением ā по базису , существует другое .

Вычитая, находим .

Так как векторы ē₁, ē₂, …, ē_n - линейно независимы, то последнее равенство имеет место только тогда, когда .

Таким образом, μ_i=γ_i для , а следовательно, разложение вектора по базису единственно.

Всякий базис линейного пространства, векторы которого берутся в определенной последовательности, называют системой координат, а числа - коэффициенты в разложении любого вектора ā по базису - называют координатами вектора ā.

ā=x₁ē₁+…+x_nē_n,

где х₁,…., х_n - координаты вектора ā.

Последнее выражение называют формулой разложения вектора по базису.

В общем случае при изменении базиса, координаты вектора изменяются.

Вектор можно задавать с помощью координат ā=(x₁,x₂,…,x_n).

Рассмотрим два вектора:

ā=(x₁,x₂,…,x_n) и =(γ₁ , γ₂ , …, γ_n).

Используя определение линейного пространства, покажите что:

1) при сложении векторов их соответствующие координаты складываются:

ā+= (x₁+γ₁ , x₂+γ₂ , …, x_n+γ_n);

2) при умножении вектора на скаляр λ, каждая координата умножается на это число: λ ā=(λx₁ , λx₂ , …, λx_n).

4.4 Евклидово пространство

Для n-мерного линейного пространства введем понятие длины вектора и угла между векторами. Это можно сделать, если определить операцию произведения над векторами.

В линейном пространстве L задано скалярное произведение, если каждой паре векторов поставлено в соответствие число такое, что:

1^о.

2^о. λ - скаляр;

3^о.

Линейное пространство L называется евклидовым пространствам, если в нем определено скалярное произведение и для любого вектора, его скалярный квадрат будет положительным.

4°. при то ā=0

Обозначают n-мерное евклидово пространство Еⁿ.

Таким образом, линейное пространство будет евклидовым, если введенное там (как угодно) скалярное произведение векторов будет удовлетворять четырем аксиомам 1°, 2°, 3°, 4°.

Пусть векторы заданы своими координатами

ā=(x₁,x₂,…,x_n) и =(γ₁ , γ₂ , …, γ_n).

Легко проверить (проверьте!), что всем аксиомам будет удовлетворить скалярное произведение, определенное как сумма произведений соответствующих координат перемножаемых векторов

или .

Нормой (длиной) вектора ' называется число, равное

или

в координатной форме

Угол между векторами определяется по формуле

Покажем, что это определение корректно, то есть выполняется условие

Пусть λ - любое действительное число, .

Согласно аксиоме 4°, имеем используя аксиомы 1°-3°, последнее неравенство можно записать в виде

Это квадратное неравенство относительно λ справедливо, если его дискриминант неположительный, то есть,

или

Итак, доказали, что для любых справедливо неравенство -оно называется неравенством Коши-Буняковского. Из неравенства Коши-Буняковского следует: или

итак, действительно

Как уже отмечалось, в n-мерном линейном пространстве базисом является любая система из n линейно независимых векторов. Часто выбирают базис из взаимно перпендикулярных (ортогональных) единичных векторов.

Базис ē₁, ē₂, …, ē_n в пространстве Еⁿ называется ортонормированным, если имеет место:

В частности, в пространстве Е² ортонормированным базисом является система двух векторов, их обозначают i, j:

в пространстве E³ ортонормированный базис обозначают i, j, k:

очевидно, что и

Пример 18. Дан треугольник АВС. где А(1, 2); В(0, 3); С(-2, -1). Найти

периметр его и угол А.

Решение

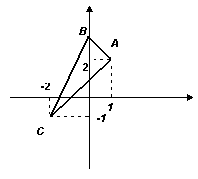
Обозначим векторы . Используя скалярное произведение, найдем . Координаты вектора ā находим, вычитая из координат его конца - точки С, соответствующие координаты начала его точки А.

Аналогично,

Найдем

Таким образом,

Чтобы найти периметр ΔАВС, надо найти длины всех его сторон:

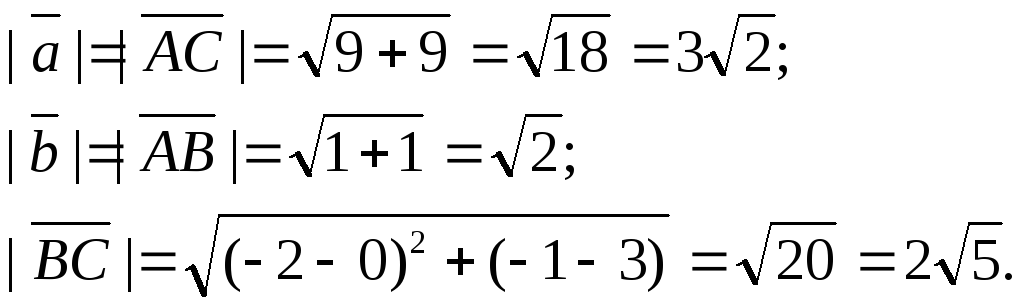
Итак, периметр ΔАВС равен