Лекция17 Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью

Рассмотрим уравнение второго порядка

,

где коэффициенты – числа, .

Согласно теореме о структуре общего решения, оно имеет вид:

,

где – общее решение однородного дифференциального уравнения,

–частное решение неоднородного дифференциального уравнения.

Вид функции устанавливается по виду правой части дифференциального уравнения.

Сначала, как и при методе Лагранжа, находится общее решение однородного дифференциального уравнения

,

его характеристическое уравнение имеет вид

,

где – его корни.

Затем отыскивается частное решение неоднородного уравнения Рассмотрим некоторые частные случаи:

1. пусть правая часть уравнения имеет вид

,

тогда частное решение определяется следующим образом:

, если ,

, если ,

, если ,

где А – неопределенный коэффициент, находится методом неопределенных коэффициентов (см. пример).

2) пусть правая часть имеет вид

где – многочлен степени , тогда частное решение определяется следующим образом:

, если ,

, если ,

, если ,

где А,B,C…D – неопределенные коэффициенты, находятся методом неопределенных коэффициентов (см. пример).

В частности, если правая часть имеет вид

где – многочлен степени , тогда частное решение определяется следующим образом:

, если ,

, если ,

, если .

3) пусть правая часть имеет вид

или

,

тогда частное решение определяется следующим образом:

, если ,

, если .

В частности, если правая часть имеет вид

или ,

тогда частное решение определяется следующим образом:

, если ,

, если .

4) пусть правая часть имеет вид

,

тогда частное решение определяется следующим образом:

,

где; если

Пример 28 Записать вид частного решения следующих дифференциальных уравнений:

1. ; б) ;

3. ; г) .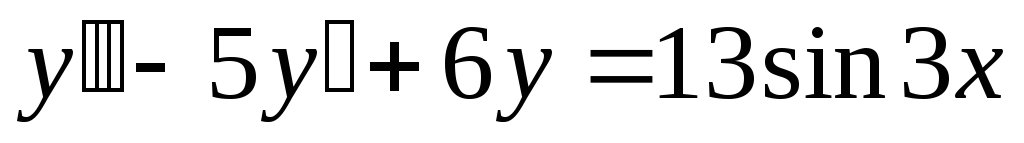

Решение:

а) .

Решаем соответствующее однородное уравнение .

Составляем характеристическое уравнение: , находим корни:;;.

Общее решение однородного уравнения .

Правая часть исходного уравнения имеет вид: ;;.

Т.к. число не является корнем характеристического уравнения, а– многочлен первой степени, то частное решение уравнения имеет вид:

.

г) .

Решаем соответствующее однородное уравнение , находим корни.

Общее решение однородного уравнения: .

Правая часть исходного уравнения имеет вид: , отсюда ,.

Т.к. число не является корнем характеристического уравнения, аи– многочлены нулевой степени, то частное решение уравнения имеет следующий вид:

.

Выполнить примеры б, в самостоятельно.

Пример 29 Решить следующие дифференциальные уравнения:

1. ; б) ;

3. .

Решение:

а) Решаем соответствующее однородное уравнение:

.

Составляем характеристическое уравнение , находим корни;.

Общее решение однородного уравнения .

По виду правой части , находим частное решение

,

число .

Методом неопределённых коэффициентов найдём .

; .

Подставим в исходное уравнение: .

Получим

,

тогда частное решение .

Общее решение исходного дифференциального уравнения

б) ;;.

Данная задача является задачей Коши, требуется найти частное решение, удовлетворяющее исходному уравнению и поставленным начальным условиям.

Решаем соответствующее однородное уравнение:

.

Составляем характеристическое уравнение ,

находим корни ;.

Общее решение однородного уравнения .

По виду правой части – многочлену второй степени , находим частное решение.

Число является корнем характеристического уравнения, а– многочлен второй степени, тогда частное решение имеет вид:

.

Методом неопределённых коэффициентов найдём ,,.

Так как

;

,

то подставляя в исходное уравнение, получим

.

После приведения подобных: .

Приравняв коэффициенты при одинаковых степенях у многочленов, стоящих в левой и правой части равенства, получим систему:

решая ее, найдем

Отсюда частное решение .

Общее решение .

Найдём частное решение, удовлетворяющее начальным условиям.

В общее решение подставим .

Чтобы удовлетворить второму условию , найдём

.

Положим ,. Получим.

Получим систему:

Частное решение .

в) .

Решаем соответствующее однородное уравнение .

Его характеристическое уравнение .

Правая часть исходного уравнения имеет вид:

,

следовательно, ;.

не является корнем характеристического уравнения. Многочлены – многочлены нулевой степени, поэтому частное решение ищем в виде:

.

Методом неопределённых коэффициентов найдём и.

;

.

Подставим в исходное уравнение:

;

.

Приравниваем коэффициенты при одинаковых тригонометрических функциях:

; ;

; .

Найдено частное решение .

Общее решение .

Пример 30 Решить уравнение

Решение:

Общее решение однородного уравнения будет

Частное решите неоднородного уравнения будем искать в виде суммы двух частных решений, так как правая часть есть сумма функций :

Подставляя в исходное уравнение получим:

Приравнивая коэффициенты при подобных членов в обеих частях уравнения получим:

итак, общее решение имеет вид