2.1.6 Несобственные интегралы

При введении понятия определённого интеграла мы предполагали, что подынтегральная функция является ограниченной, а пределы интегрирования – конечными. Такой интеграл называется собственным (слово «собственный» обычно опускается). Если хотя бы одно из этих двух условий не выполнено, то интеграл называется несобственным.

Интегралы с бесконечными пределами интегрирования

Пусть функция f(x) непрерывна при <, т.е. приТогда по определению полагают

Если этот предел существует, то говорят, что интеграл

сходится, а если предел не существует, то интеграл называют расходящимся.

Геометрически для неотрицательной при функцииf(x) несобственный интеграл по аналогии с собственным интегралом представляет собой площадь фигуры, ограниченной сверху графиком функции y=f(x), слева отрезком прямой x=a и снизу осью Ox.

Пример 13 Исследовать на сходимость интегралы:

а) т.е. данный несобственный интеграл сходится.

б) т.е. данный интеграл расходится.

в) Установим, при каких значениях интегралсходится.

Случай был рассмотрен в примере б). Еслито

.

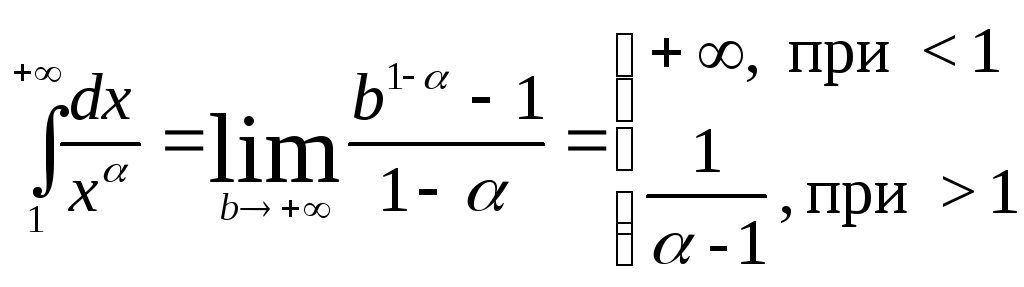Значит, данный интеграл сходится при >1 и расходится при

Аналогично определяются следующие несобственные интегралы

Интегралы от неограниченных функций

Пусть функция f(x) непрерывна при <b. Пусть эта функция стремится к бесконечности, когда(т.е. на отрезкефункцияf(x) не ограничена). Положим

Если этот предел существует, то говорят, что интеграл

сходится, а если предел не существует, то интеграл называют расходящимся.

Подобным же образом равенство

даёт определение интеграла от функции f(x), стремящейся к бесконечности при

Наконец, если функция f(x) стремится к бесконечности при приближении аргумента к обоим концам промежутка , то полагают

a<c<b.

Если при этом сходятся оба интеграла в правой части последнего равенства, то сходится и интеграл слева.

Пример 14

, т.е. расходится.

Лекция 14 дифференциальные уравнения

2.2.1 Основные понятия. Дифференциальные уравнения первого порядка. Задача Коши.

Обыкновенным дифференциальным уравнением n^-го порядка называется выражение вида:

или ,

то есть, уравнение, содержащее неизвестную функцию и её производные доn^-го порядка.

Так, например:

1. , или 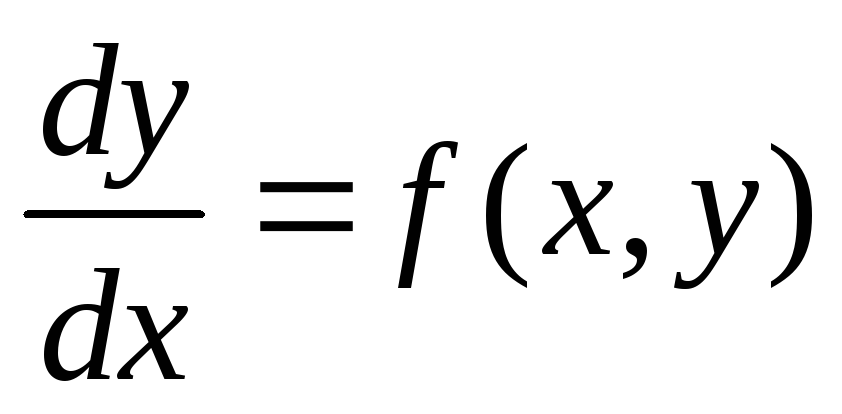- это дифференциальное уравнение первого порядка;

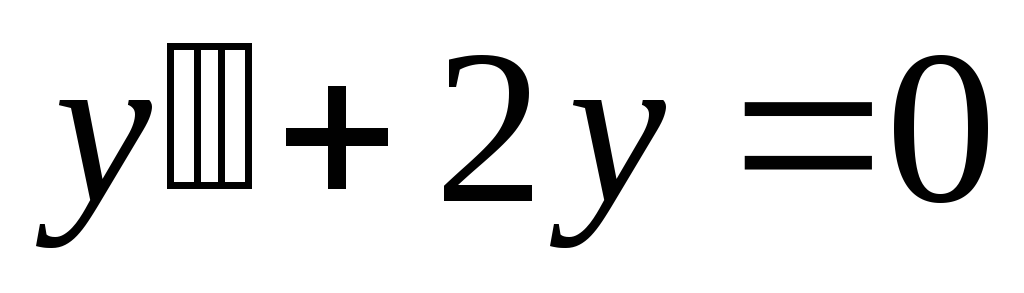2. - дифференциальное уравнение второго порядка.

Из определения дифференциального уравнения следует, что его порядок равен порядку старшей производной, содержащейся в нём.

Решением дифференциального уравнения называется любая функция

,

которая при подстановке в уравнение обращает его в тождество.

Пример 16 Проверить (самостоятельно), будут ли функции

; ;;

решениями дифференциального уравнения

.

Решение:

Рассмотрим уравнения первого порядка.

(1)

имеет место следующая

теорема Коши

Если функция определена и непрерывна в областивместе со своей частной производной, то для всякой точки, принадлежащей области, в некоторой её окрестности, существует единственное решение, удовлетворяющее начальному условию при

. (2)

Условия (2) называются начальными условиями.

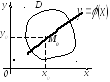
Геометрически это означает, что при выполнении условий теоремы через каждую внутреннюю точку M₀ области проходит единственная интегральная кривая.

Задачей Коши называют задачу о нахождении решения дифференциального уравнения

, (1)

удовлетворяющее начальным условиям

. (2)

Вышеприведённую теорему называют теоремой о существовании и единственности решения задачи Коши.

Общим решением дифференциального уравнения первого порядка называют функцию такую, что

1. при любом она является решением дифференциального уравнения (1);

2. каковы бы ни были начальные условия (2), всегда можно найти такое 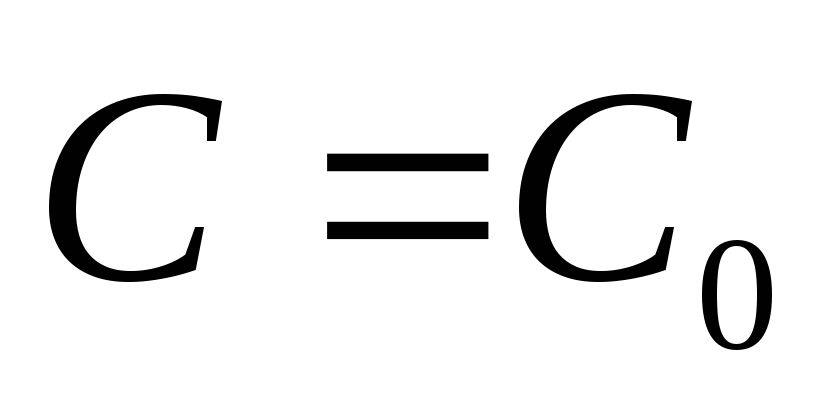, что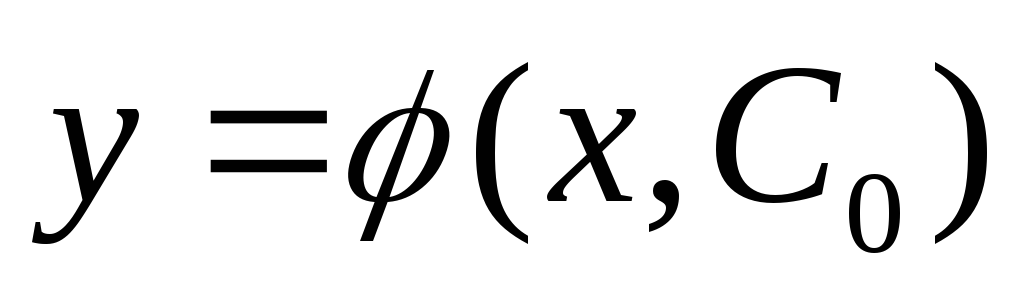удовлетворяет начальным условиям (2).

Частным решение называется решение, полученное из общего при конкретном значении .