Лекция16 Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Однородное дифференциальное уравнение второго порядка имеет вид
,
где
– числа,
.
Если функции
образуют фундаментальную систему
решений, то общее решение дифференциального
уравнения имеет вид:
.
Предположим, что частные решения имеют вид:
.
Найдём производные:
,
и подставим в исходное дифференциальное уравнение
или
,
т.к.
,
то
.
Данное уравнение называется характеристическим уравнением.
При решении квадратного уравнения возможны три случая:
1)
,различные
действительные корни,
если дискриминант
.
Фундаментальную систему решений
составляют функции:
,
общее решение имеет вид:
.
2) корни
действительные, равные,
,
если дискриминант
.
Фундаментальную систему решений
составляют функции:
,
общее решение имеет вид:
.
3) корни
комплексные числа,
,
если дискриминант
.
Фундаментальную систему решений
составляют функции:
,
общее решение имеет вид:
.
Пример 26 Решить
а)
; б)
; в)
.
Решение:
а) составим характеристическое уравнение:
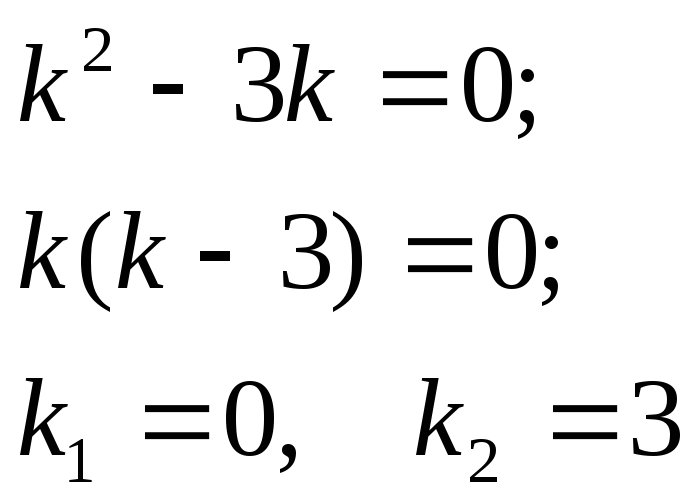
общее решение имеет вид:
или
.
б) составим характеристическое уравнение:
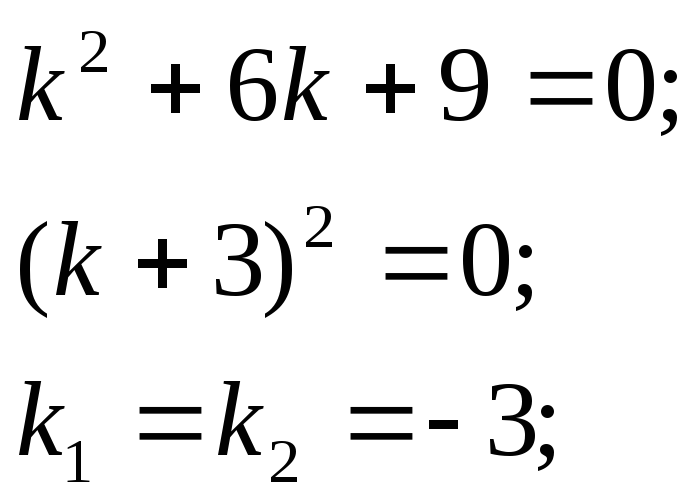
общее решение имеет вид:
.
в) составим характеристическое уравнение:
,
где
.
Итак,
,
комплексные числа, где
.
общее решение имеет вид:
.
16.1 Линейные неоднородные дифференциальные уравнения. . Метод Лагранжа
Рассмотрим линейное неоднородное дифференциальное уравнение
где
непрерывная функция. Однородное уравнение
соответствующее неоднородному уравнению
будет
Справедлива следующая теорема о структуре общего решения линейного неоднородного дифференциального уравнения:
Если
– частное решение уравнения
а
– общее решение однородного уравнения
то общее решение неоднородного уравнения
равно сумме частного решения неоднородного
уравнения и общего решения однородного
уравнения
Замечание.
Если правая часть
уравнения
есть сумма нескольких функций
,
то частное решение уравнения равно
сумме частных решений, отвечающих каждой
функции в отдельности
.
Как мы убедились
раньше, задача отыскания общего решения
неоднородного уравнения
сводится к отысканию общего решения
однородного уравнения
и частного решения неоднородного
уравнения
.
Приведем метод, позволяющий определить общее решение неоднородного уравнении по общему решению однородного уравнения.
Метод Лагранжа (метод вариации постоянных) решения линейного неоднородного дифференциального уравнения второго порядка
Алгоритм метода:
Решить однородное уравнение
и записать его общее решение
Записать общее решение неоднородного уравнения, полагая произвольные константы функциями от x:
,
тогда
3. Записать систему уравнений
и решить ее.
4.
Полученное решение
подставить в
.
Пример 27 Решить
уравнение
Решение:
Для соответствующего
однородного уравнения
общее решение имеет вид
Запишем его в виде
составляем систему
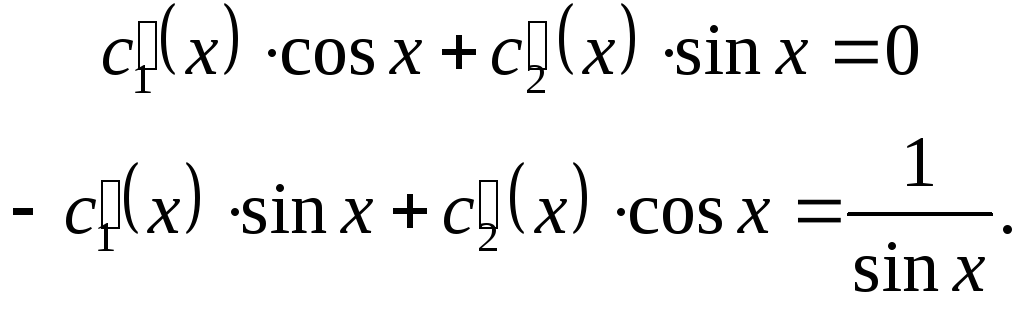
Решаем эту систему по методу Крамера:
,
где
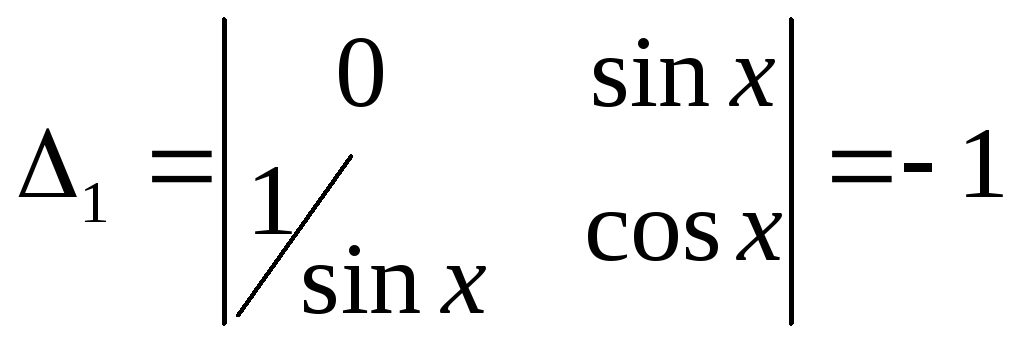
получим
Интегрируя, найдем
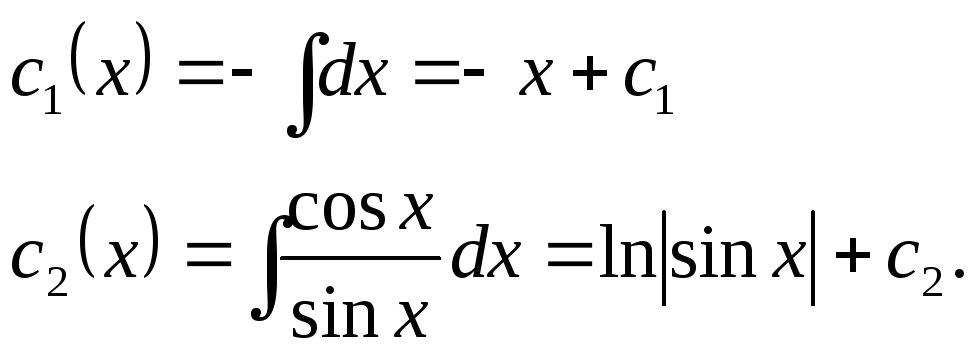
Подставляя
найденные
в общее решение однородного дифференциального уравнения
,
получим
.