2.2.2 Простейшие типы дифференциальных уравнений первого порядка.

1. Уравнение с разделёнными переменными

или

.

Решая первое уравнение, получим .

Интегрируя, найдём общее решение .

Решая второе, получим .

Интегрируя, найдём общее решение.

2. Уравнение с разделяющимися переменными,

или

.

Разделим обе части первого уравнения наи умножим на, получим уравнение с разделёнными переменными

Для второго уравнения: разделим обе части на произведение , получим также уравнение с разделёнными переменными

.

Операция деления уравнения на произведение называетсяразделением переменных.

При делении на произведение можно потерять некоторые решения, которые получаются из уравнения

.

Определяя из этого уравнения решения , следует проверить, является ли оно решением исходного уравнения. Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называетсяособым.

Пример 17 Решить уравнение .

Решение:

Разделим уравнение на произведение , получим:

.

Интегрируя, получим общий интеграл:

.

В этом уравнении имеет вид. Его решение,является решением исходного уравнения, но не входит в общий интеграл. Следовательно, решение,является особым.

Пример 18 Найти общее решение .

Решение:

;

;

интегрируя, найдем общее решение

или ;

;

;

3. Однородные уравнения.

Функция называетсяоднородной степени , если для любых ивыполняется равенство

Если функции иоднородные одной и той же степени, то дифференциальное уравнениеназываетсяоднородным.

Однородное уравнение всегда можно привести к виду

,

решается подстановкой:

или ;.

Пример 19 Решить .

Решение:

Данное уравнение является однородным, т.е. функции ,однородные степени. Сделаем замену Тогда уравнение перепишется так:

;

;

разделяя переменные, получим:

;

;

;

Так как у нас , то,,.

Лекция15

Линейные дифференциальные уравнения

Уравнение ,

где ,- непрерывная функция отна интервале, называетсялинейным дифференциальным уравнением первого порядка.

Неизвестная функция и её производная входят в это уравнение в первой степени – линейно.

Линейные уравнения обычно решают методом Бернулли.

Представим искомую функцию в виде произведения двух неизвестных функций и.

Пусть , тогдаили,

и уравнение примет вид

или .

Полученное уравнение разобьём на два таким образом:

1. Выберем функцию 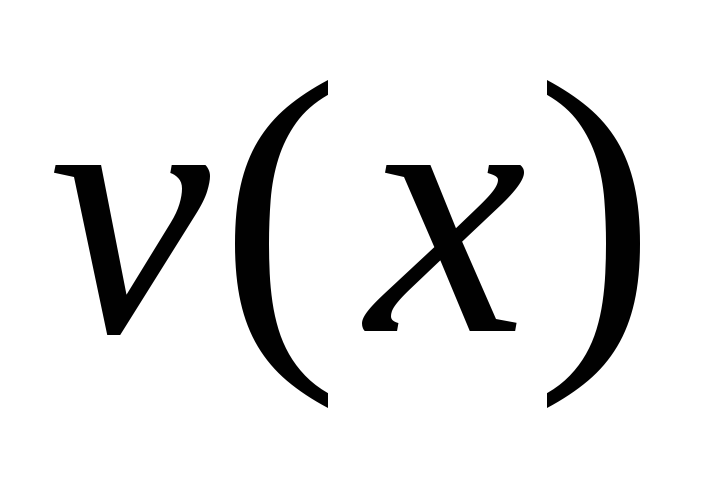так, чтобы сумма второго и третьего слагаемых обратилась в нуль:

;

2. .

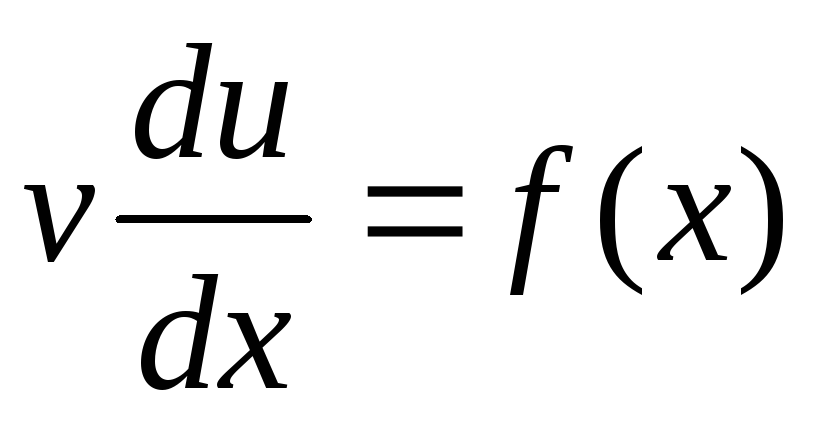Решаем первое: так как , относительноимеем уравнениес разделяющимися переменными:

или

Функцию подставим во второе уравнение:

, откуда .

.

Найдём общее решение по формуле

,

подставив найденные функции вместо ,.

Пример 20 Решить уравнение .

Решение:

Положим ,.

Подставляя выражения для ив данное уравнение получим:

1)

2) .

Решаем первое уравнение:

После разделения переменных получим . Отсюдаили.

Решаем второе уравнение:

Подставим найденное значение , получим:

.

Отсюда, разделяя переменные и интегрируя, находим функцию :

.

Теперь можно записать общее решение данного дифференциального уравнения:

или

.

4. Уравнением Бернулли

называется уравнение вида

,

где – любое вещественное число.

Если равно нулю или единице, то мы получим линейное дифференциальное уравнение.

Уравнение Бернулли можно сразу решать методом Бернулли, полагая . Следует отметить, что прифункцияявляется решением Бернулли.

Пример 21 Решить уравнение .

Решение:

Приведём решение методом Бернулли.

Полагая

;

;

получим

1) ;;;.

2) Подставим найденную функцию :

; ;;;;

и окончательно .