
- •Лекция 10
- •10.1 Неопределённый интеграл, его свойства
- •Интегралы от основных элементарных функций (Таблица интегралов)
- •10.2 Методы интегрирования
- •Определённый интеграл, его свойства
- •2.1.4 Теорема Ньютона-Лейбница
- •Интегрирование по частям
- •2.1.5 Геометрические приложения определённого интеграла Вычисления площадей плоских фигур
- •2.1.6 Несобственные интегралы
- •Пример 13 Исследовать на сходимость интегралы:
- •Пример 14
- •Лекция 14 дифференциальные уравнения
- •2.2.1 Основные понятия. Дифференциальные уравнения первого порядка. Задача Коши.
- •2.2.2 Простейшие типы дифференциальных уравнений первого порядка.
- •Лекция15
- •Лекция16 Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •16.1 Линейные неоднородные дифференциальные уравнения. . Метод Лагранжа
- •Лекция17 Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью
- •Лекция18
- •Свойства сходящихся числовых рядов
- •2.3.2 Достаточные признаки сходимости рядов
- •Лекция19 Знакопеременные ряды. Признак Лейбница
- •Пример 37 Исследовать ряд на сходимость.
- •2.3.4 Функциональные ряды. Степенные ряды
- •Разложение функций в степенные ряды. Ряды Тейлора, Маклорена
- •Применение рядов в приближенных вычислениях
Лекция 10
10.1 Неопределённый интеграл, его свойства
Первообразная функция и неопределённый интеграл
Функция F(x) называется первообразной функцией для данной функции f(x) на данном промежутке, если на этом промежутке
![]() .
.
Например, функция F(x)=x3 является первообразной функции f(x)=3x2 на всей числовой оси, так как (x3)/=3x2 при любом x. Отметим, что вместе с функцией F(x)=x3 первообразной для f(x)=3x2 является любая функция вида Ф(х)=х3+С, где С – произвольное постоянное число.
Лемма о первообразных
Если F1(x) и F2(x) – две первообразные для функции f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.
Из этой теоремы следует, что если известна какая-нибудь первообразная F(x) данной функции f(x), то всё множество первообразных для f(x) можно записать в виде F(x)+C.
Выражение F(x)+C,
где F(x)
– первообразная функции f(x)
и С
– произвольная постоянная, называется
неопределённым
интегралом
от функции f(x)
и обозначается символом
![]() ,
причёмf(x)
называется подынтегральной
функцией,
f(x)dx
– подынтегральным
выражением,
,
причёмf(x)
называется подынтегральной
функцией,
f(x)dx
– подынтегральным
выражением,
х
– переменной
интегрирования;
![]() –знак
неопределённого интеграла.
–знак
неопределённого интеграла.
Таким образом, по определению
![]()
если
![]() .
.
Возникает вопрос: для всякой ли функции f(x) существует первообразная, а значит, и неопределённый интеграл?
Свойства неопределённого интеграла
Производная от неопределенного интеграла равна подынтегральной функции
![]()
Дифференциал неопределенного интеграла равен подынтегральному выражению
![]()
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого
![]() или
или
![]()
где С – произвольное число
Постоянный множитель можно выносить за знак интеграла
где k – некоторое число.
Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций
![]()
Интегралы от основных элементарных функций (Таблица интегралов)

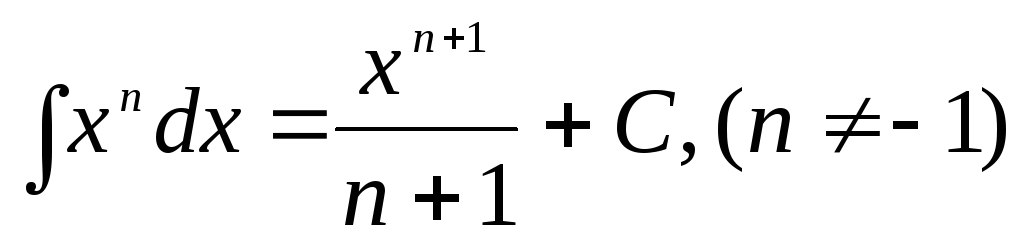 .
.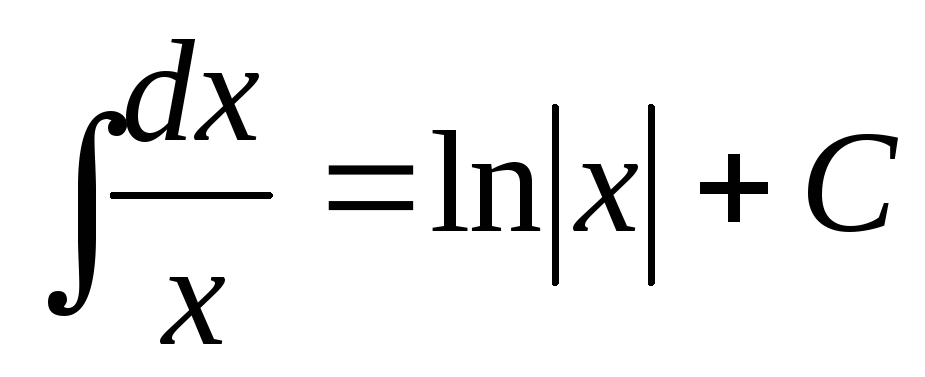 ,
в общем случае
,
в общем случае
 ,
в частности
,
в частности
 9)
9)
 10)
10) 
 11)
11) 
 12)
12) 
10.2 Методы интегрирования
![]() Метод
непосредственного интегрирования
связан с приведением подынтегрального
выражения к табличной форме путём
преобразований и применения свойств
неопределённого интеграла.
Метод
непосредственного интегрирования
связан с приведением подынтегрального
выражения к табличной форме путём
преобразований и применения свойств
неопределённого интеграла.
Пример 1.
Найти интеграл
![]()
Решение:
![]() .
.
Пример 2. Найти
интеграл
![]()
Решение:
![]()
![]() Замена
переменной интегрирования
Замена
переменной интегрирования
Если
![]() ,
где
,
где![]() -
функция, имеющая непрерывную производную,
тогда
-
функция, имеющая непрерывную производную,
тогда![]() ;
подставляя в интеграл, получим
;
подставляя в интеграл, получим
![]()
![]()
Пример 3. Найти
интеграл
![]()
Решение:
Воспользуемся
подстановкой x=t2.
Тогда
![]() ,
получим
,
получим
![]()
![]() Интегрирование
по частям
Интегрирование
по частям
Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции. Тогда справедлива формула
![]() .
.
Пример 4.
Найти интеграл
![]()
Решение:
Пусть u=x
![]() du=dx,
du=dx,
![]() ;
Используя формулу интегрирования по
частям, получим
;
Используя формулу интегрирования по
частям, получим
![]()
Лекция 11
Интегрирование простейших рациональных дробей
Многочленом степени
n
называется выражение вида
![]() ,
где
,
где![]() – действительные числа
– действительные числа![]() .
Например, 5–7x
– многочлен первой степени
.
Например, 5–7x
– многочлен первой степени
![]() ,
,
![]() =2x3
– 3x2
+8x
– 1 – многочлен третьей степени.
=2x3
– 3x2
+8x
– 1 – многочлен третьей степени.
Рациональной
дробью называется отношение двух
многочленов. Например,
![]() – рациональные дроби. Всякая рациональная
дробь имеет вид:
– рациональные дроби. Всякая рациональная
дробь имеет вид:
![]()
где
![]() – многочлены степени m
и n
соответственно.
– многочлены степени m
и n
соответственно.
![]() ,
если
,
если

![]()
![]()
Простейшими рациональными дробями являются следующие четыре типа дробей:
I)![]() ;II)
;II)![]() III)
III)![]() ;IV)
;IV)![]()
Очевидно, что интегралы от простейших дробей первого и второго типов находятся легко:
![]() ,
,
![]()
где k
– целое,
![]() .
.
От дробей третьего
и четвёртого типов вычисляют заменой
![]() ,или по
следующим формулам:
,или по
следующим формулам:
![]()
![]()
![]() Разложение
многочленов на множители
Разложение
многочленов на множители
Для любых многочленов
![]() имеет место теорема
Безу:
имеет место теорема
Безу:
![]() ,
где z0
простой корень
,
где z0
простой корень
![]() ,
где z0
корень кратности k.
,
где z0
корень кратности k.
Если z
корень комплексный:
![]() ,
гдеi=
,
гдеi=![]()
и
![]() ,
то
,
то![]() ,
где
,
где![]() – сопряженный корень.
– сопряженный корень.
Любой многочлен можно разложить на линейные и квадратичные множители
![]()
![]()
![]() –действительные
корни;
–действительные
корни;
![]()
комплексные корни
комплексные корни
Правильную
рациональную дробь можно разложить на
сумму простейших дробей,
если знаменатель дроби
![]() представлен в виде сомножителей
представлен в виде сомножителей
![]() :
:

Пример 5. Разложить на сумму простейших дробей следующие дроби:
а)
![]() ;
;
б)
![]() .
.
Решение:
а)
![]()
б)
![]()
Пример 6. Вычислить интеграл:
![]()
Решение:
Разложим подынтегральную дробь на простейшие дроби
![]()
приравнивая числители дробей, получаем:
![]()
Определим коэффициенты А и В, придавая любые значения переменной x:
![]()
Получаем А=1 и В=1. Исходный интеграл найдём как сумму интегралов от полученных дробей.
![]()
Лекция 12
Интегрирование тригонометрических функций
![]() Рассмотрим интегралы
вида
Рассмотрим интегралы
вида
![]() .
Такие интегралы могут быть сведены к
интегралам от рациональных функций
заменой переменной
.
Такие интегралы могут быть сведены к
интегралам от рациональных функций
заменой переменной
![]() ,
где
,
где![]()
Такая замена называется универсальной тригонометрическая подстановкой.
В этом случае,
![]()
![]()
![]()
Тогда
![]() .
.
Пример 7.
Найти
![]()
Решение:
Положим
![]() .
Тогда, используя выражения черезt
для dx
и sinx,
указанные выше, получаем, что искомый
интеграл равен
.
Тогда, используя выражения черезt
для dx
и sinx,
указанные выше, получаем, что искомый
интеграл равен
![]()
![]() При вычислении
интегралов вида
При вычислении
интегралов вида
![]()
рассмотрим частные случаи:
n – нечётное
![]()
n,
m
– чётные,
![]() .
.
![]()
применяют формулы тригонометрии:
![]()
![]()
![]() При вычислении
интегралов вида
При вычислении
интегралов вида
![]() делают замену
делают замену
![]() ,
тогда
,
тогда
![]()
![]()
![]()
![]() Если
интеграл имеет
вид
Если
интеграл имеет
вид
![]() ,
,
где n, m – чётные, применяют формулу:
![]()
Пример 8. Вычислить интегралы:
а)
![]()
б)
![]()
Решение:
а)
![]()
б)
![]()
![]() При вычислении
При вычислении
![]()
![]()
![]()
используют формулы
![]()
![]()
![]()
![]() Интегрирование
иррациональных выражений
Интегрирование
иррациональных выражений
При вычислении интегралов, содержащих иррациональные выражения применяют замену переменной.
Если
![]() ,
,
то
![]() , где
, где![]()
![]()
Если

то
![]() , где
, где![]()
Лекция13
