
Корректирующие устройства
Для того, чтобы добиться желаемого качества процесса управления, т.е. требуемой точности и качества переходного процесса есть два способа.
Прежде всего, необходимо попытаться рациональным способом изменить ее параметры (коэффициенты отдельных звеньев, постоянные времени и т.п.). При этом изменяться частотные характеристики, а значит, качество процесса.
При невозможности решить эту задачу в рамках имеющейся системы, надо изменять ее структуру. Для этой цели обычно используется введение в систему корректирующих устройств, которые должны изменить динамику всей системы.
Различают следующие виды корректирующих устройств.
-
Последовательные корректирующие устройства (корректирующие фильтры).
-
Параллельные корректирующие устройства.
Последовательные корректирующие устройства
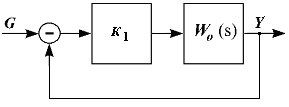
Последовательные корректирующие устройства (корректирующие фильтры), которые могут быть описаны различными передаточными функциями. Тогда общая передаточная функция разомкнутой системы будет W(s)=Wk(s)Wo(s). (рис.а). Или общая передаточная функция системы будет W(s)=Wk(s)Wo(s)=(Wo1(s)+Wk1(s))Wo(s) (рис.б)
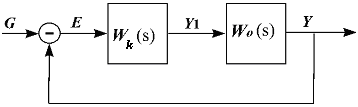
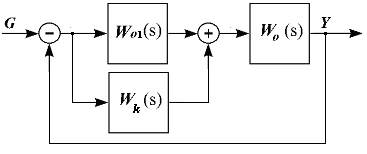
а б
-
Введение производной от ошибки – простейший способ улучшения качества переходного процесса. Структурно это показано на рис.
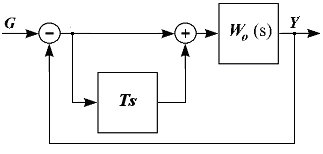
Передаточная
функция разомкнутой цепи будет:
![]() .
.
Амплитуда и
фаза: ![]()
![]() .
.
При введении воздействия по производной добавляется положительная фаза. Вследствие этого радиус-вектор АФЧХ поворачивается против часовой стрелки, увеличивая запас устойчивости и улучшая качество переходного процесса.
Введение производной от ошибки служит стабилизирующим средством. Например, если точка –1 лежала бы внутри характеристики Wo(j) , то новая характеристика W(j) уже могла бы не охватывать точку –1.
Можно ввести
дифференцирование с запаздыванием
![]() .
.
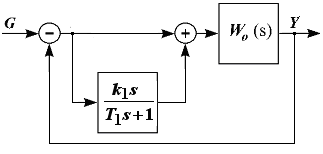
В этом случае
эффект уменьшиться количественно, но
качественно остается. Звено
![]() является инерционным и имеет хорошие
фильтрующие свойства.
является инерционным и имеет хорошие
фильтрующие свойства.
-
Увеличение общего коэффициента усиления К разомкнутой цепи.
Повышается точность системы. Увеличение К=К1Ко осуществляется последовательным введением усилительного звена в общую цепь. Но увеличение К ведет к ухудшению условия устойчивости, а значит, качества переходного процесса. Поэтому применяется одновременно с введением производной.
-
Введение интеграла от ошибки. Повышает порядок астатизма системы, значит, увеличивается ее точность.
Передаточная
функция разомкнутой цепи:
![]() .
.
Амплитуда и
фаза: ![]()
![]() .
.
Вследствие поворота фазы на –90 град. ухудшаются условия устойчивости и качества переходного процесса. Это может привести к неустойчивости замкнутой системы.
-
Изодромное корректирующее устройство имеет передаточную функцию:
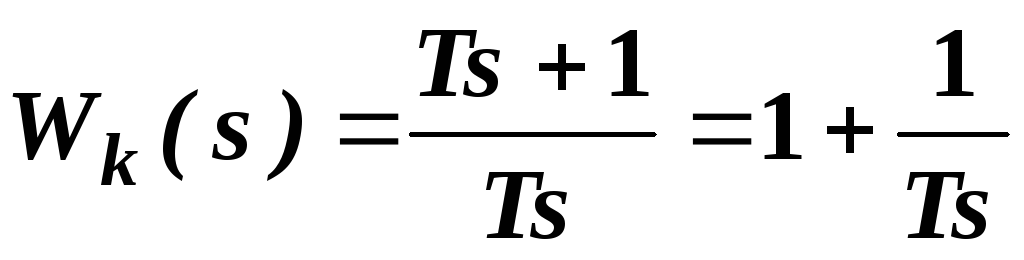 .
.
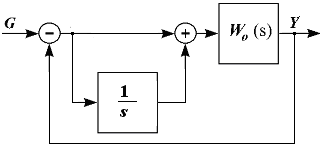
Структурно устройство представлено на рис.
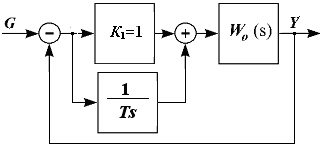
Получаем регулирование по ошибке и по интегралу от ошибки. Это устройство позволяет избежать недостатков предыдущего устройства и получить необходимый порядок астатизма, сохраняя устойчивость и качество системы.
Последовательные корректирующие устройства еще называют ПИД-регулятором.
Первая составляющая ПИД-регулятора представляет собой пропорциональное звено (П), вторая составляющая – интегрирующее звено (И), третья составляющая – дифференцирующее звено (Д). На основании этого последовательное корректирующее устройство имеет название ПИД-регулятор.
Управляющий сигнал
x1
в последовательных
корректирующих устройствах формируется
следующим образом:
![]() ,
где k1,
k2,
k3 – постоянные.
,
где k1,
k2,
k3 – постоянные.
Существуют также П-, ПИ-, ПД-регуляторы, структура которых составляется соответственно тому, какие составляющие включены в последовательное корректирующее устройство.
Параллельные корректирующие устройства
Параллельные корректирующие устройства осуществляются за счет дополнительных местных обратных связей Woс(s).
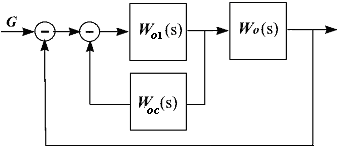
Общая передаточная
функция такой системы
![]() .
.
Основные виды корректирующих обратных связей:
-
Жесткая обратная связь Woс(s)=koс
-
Инерционная жесткая обратная связь
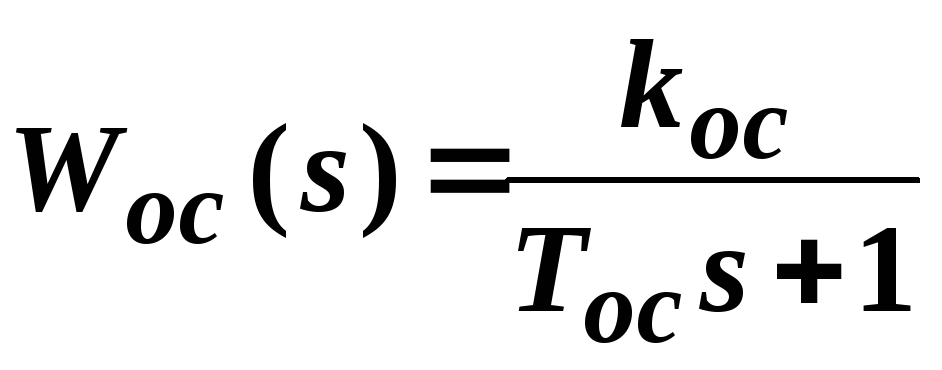
-
Гибкая обратная связь Woс(s)=koсs
-
Инерционная гибкая обратная связь
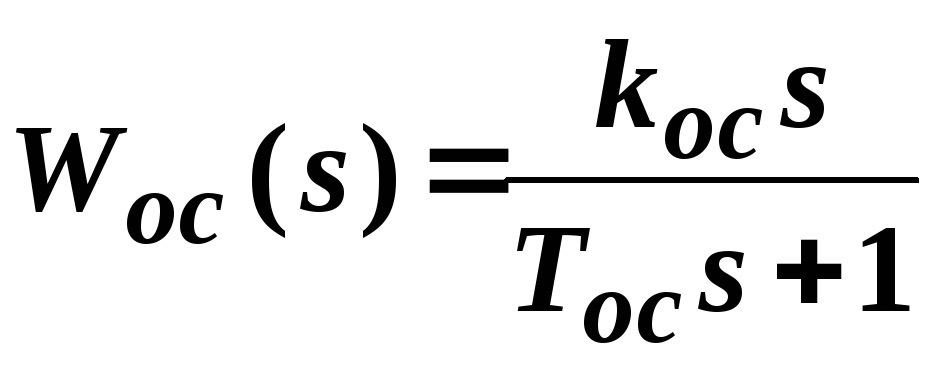
Возможны более сложные передаточные функции корректирующих обратных связей.
Положительная жесткая обратная связь
Передаточная функция такого корректирующего устройства Woс(s)=koс.
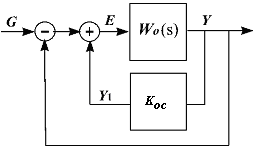
Пусть охватывает
апериодическое
звено,
передаточная функция которого
![]() .
.
Общая передаточная
функция разомкнутой цепи:
![]() .
.
Разделим на (1–koсk)
и получим
![]() ,
где
,
где![]() ,
,
![]() .
.
Положительная жесткая обратная связь служит для увеличения коэффициента усиления, но при этом увеличивается и постоянная времени, но при koс>1/k звено становится неустойчивым (Т1<0).
Отрицательная жесткая обратная связь
Передаточная функция корректирующего устройства Woс(s)=koс.
Пусть охватывает
апериодическое
звено,
передаточная функция которого
![]()
Общая передаточная
функция разомкнутой цепи
![]()
Разделим на (1+koсk)
и получим
![]() ,
где
,
где![]() ,
,
![]() .
.
Отрицательная жесткая обратная связь уменьшает инерционность звена (улучшает качество переходного процесса). Может неустойчивую замкнутую систему превратить в устойчивую. А уменьшение коэффициента усиления может быть скомпенсировано за счет других звеньев.
Пусть охватывает
интегрирующее
звено,
передаточная функция которого
![]() ,
,
Общая передаточная
функция разомкнутой цепи
![]()
или
![]() ,
где
,
где![]() ,
,
![]() .
.
При этом интегрирующее звено превратилось в апериодическое звеном с коэффициентом усиления, зависящим от koс, а постоянная времени Т1 мала при большом k.
В ТАУ в основном используется отрицательная обратная связь. Если специально не оговаривается, то под обратной связью будем понимать отрицательную обратную связь.
Инерционная жесткая обратная связь
Передаточная
функция инерционной жесткой обратная
связи ![]() .
.
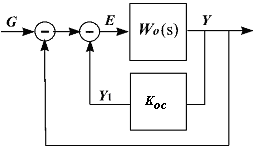
Введение такого корректирующего устройства структурно показано на рис.
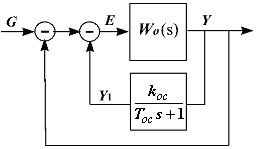
Пусть охватывает
интегрирующее
звено,
передаточная функция которого
![]() ,
,
Общая передаточная
функция
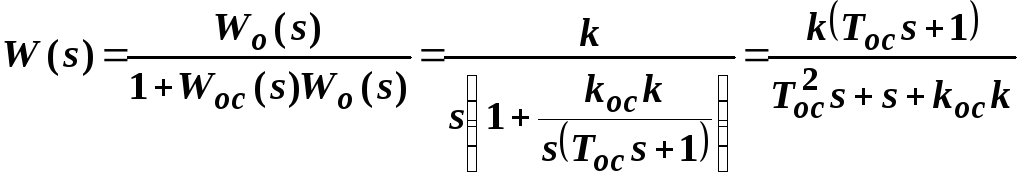
или 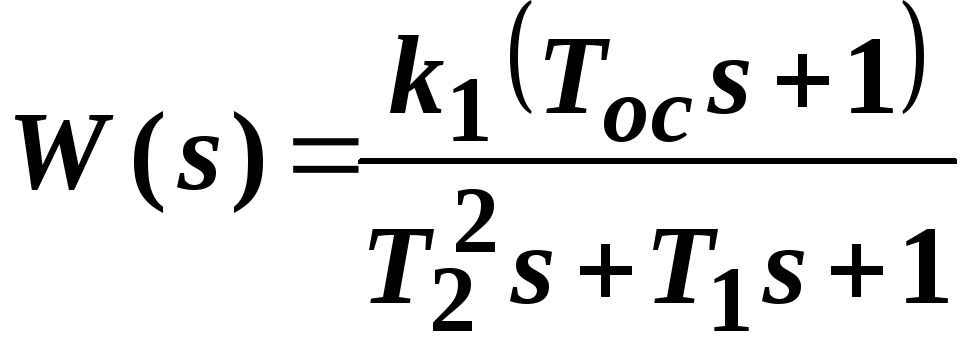 ,
где
,
где
![]() ,
,
![]()
![]() .
.
При этом интегрирующее звено превратилось в апериодическое звено второго порядка с введением производной. При этом коэффициент усиления k1 и интенсивность введения производной определяются обратной связью, а коэффициент k влияет на постоянные времени Т1 и Т2, которые тем меньше, чем больше k.
При очень большом k охват интегрирующего звена инерционной жесткой обратной связью эквивалентен усилительному звену с введением производной:
![]() .
.
Отсюда получаем хорошее влияние этой связи на качество переходного процесса в системе в целом.
Гибкая обратная связь
Гибкая обратная связь Woс(s)=koсs.
Введение такого корректирующего устройства структурно показано на рис.
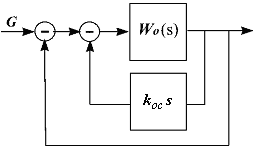
Пусть охватывает
колебательное
звено с
передаточной функцией
![]() .
.
Общая передаточная функция разомкнутой цепи
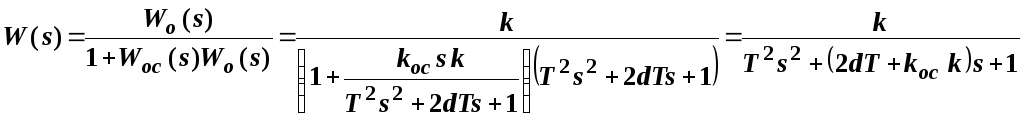
или ![]() ,
где
,
где
![]() ,
или
,
или
![]() .
.
В этом случае увеличивается демпфирование колебательного звена (т.к. d1>d), причем не меняется коэффициент усиления. Процесс становится менее колебательным и может превратиться в апериодический, если d1 1.
Охватывать гибкой
обратной связью апериодическое
звено
![]() не имеет смысла, т.к. это только увеличит
его инерционность (постоянную времени).
Общая передаточная функция разомкнутой
цепи в этом случае:
не имеет смысла, т.к. это только увеличит
его инерционность (постоянную времени).
Общая передаточная функция разомкнутой
цепи в этом случае:
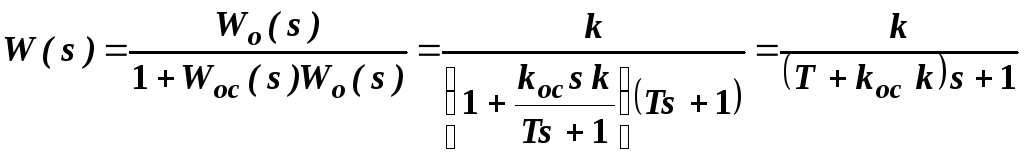 или
или ![]() ,
,
где
![]() .
.
При охвате ГОС
интегрирующего
звена
![]() получим апериодическое звено:
получим апериодическое звено:
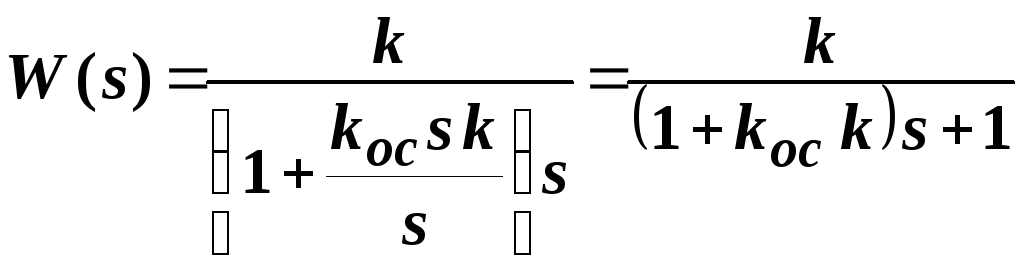 или
или ![]() ,
где
,
где
![]() .
.
При охвате ГОС
инерционного
интегрирующего звена
![]()
получим апериодическое
звено:
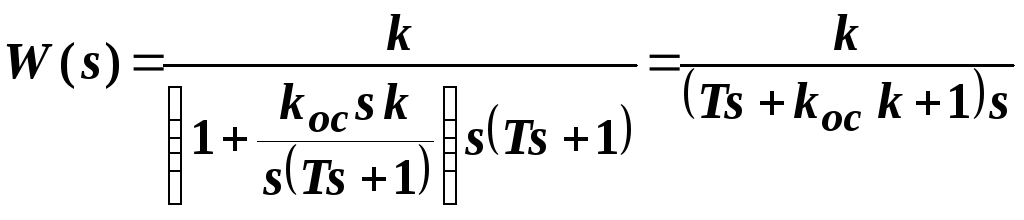
или
![]() ,
где
,
где
![]() ,
,
![]()
Звено осталось тем же, но уменьшилась инерционность.
Инерционная гибкая обратная связь
Инерционная гибкая
обратная связь ![]() .
.
Введение такого корректирующего устройства структурно показано на рис.
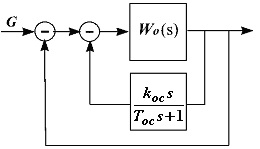
При охвате
инерционного
интегрирующего звена
![]() получим:
получим:
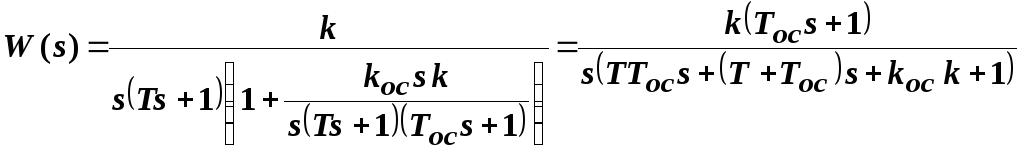
или
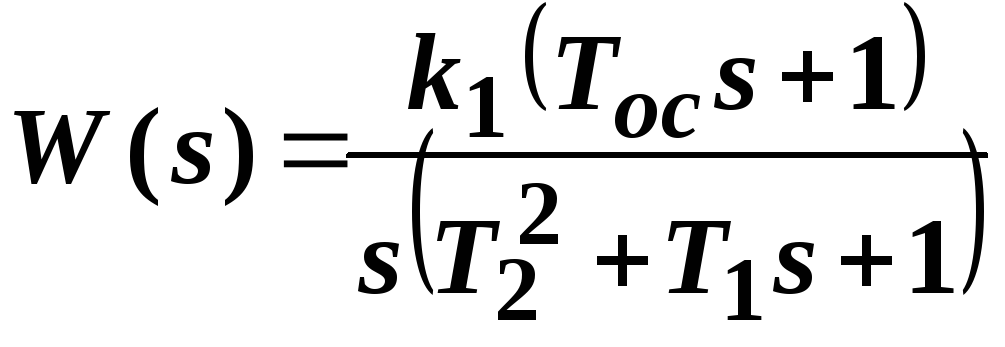 ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
.
Звено сохранило интегрирующие свойства, но появился эффект введения производной, т.е. интегрирующее звено стало изодромным, а новые постоянные времени Т1 и Т2, характеризующие инерционность звена могут быть сделаны малыми за счет большого первичного коэффициента усиления k. Тогда получим:
![]()
![]() .
.
Инерционное запаздывание в обратной связи (в отличие от такого в прямой цепи) целесообразно использовать для увеличения качества переходных процессов, получая эффект, аналогичный введению производной в прямой цепи.
Общим свойством является также и то, что жесткие обратные связи аннулируют интегрирующие свойства звена (т.е. аннулируют астатизм системы, если нет интегрирования в другом месте цепи звеньев), а гибкие обратные связи сохраняют астатизм системы.
