LR_TOY_M03062

77

9.5Обробка результатів вимірювань та оформлення звіту

9.5.1За результатами досліду 9.4.1 обчислити відношення дію-

чого значення струму I5 до постійної складової I4 та порівняти з те-

оретичним відношенням цих значень при однонапівперіодному випрямленні.

9.5.2 За результатами досліду 9.4.1 розрахувати діюче значення напруги на навантаженні Uн = U12 + U22 та порівняти з виміряним

значення цієї величини U4 .

9.5.3 За результатами досліду 9.4.3 обчислити відношення діючого значення струму I5 до постійної складової I4 та порівняти з те-

оретичним відношенням цих значень при двонапівперіодному випрямленні.

9.5.4 За результатами досліду 9.4.1 розрахувати діюче значення напруги на навантаженні Uн = U12 + U22 та порівняти з виміряним

значення цієї величини U4 .

9.5.5 Зробити висновки по роботі.

9.6Контрольні запитання

9.6.1Які функції можна розкласти у тригонометричний ряд Фу-

р'є?

9.6.2Запишіть у загальному вигляді тригонометричний ряд Фу- р'є та поясніть як визначаються його складові.

9.6.3Приладами якої системи вимірюють діючи значення струму та напруги?

9.6.4Приладами якої системи вимірюють постійні складові струму та напруги?

9.6.5Як виміряти діюче значення змінної складової напруги?

9.6.6Як розрахувати значення повної, активної та реактивної потужностей у колі несинусоїдного струму? Яким чином вони пов’язані зі значенням потужності спотворення?

9.6.7Які співвідносяться між собою постійні складові та діючи значення струмів при однонапівперіодному та двонапівперіодному випрямленні?

9.6.8Покази якого з вольтметрів на рис.9.2 найбільші? Доведіть це.

PDF created with pdfFactory Pro trial version www.pdffactory.com

78

Лабораторна робота №10

ДОСЛІДЖЕННЯ ПЕРЕХІДНИХ ПРОЦЕСІВ В ЕЛЕКТРИЧНОМУ КОЛІ З КОТУШКОЮ ІНДУКТИВНОСТІ

Мета роботи: оволодіння навичками розрахунку та дослідження електричних кіл постійного струму з котушкою індуктивності у перехідному режимі роботи.

10.1Короткі теоретичні відомості

10.1.1Основні визначення

Увипадку різних комутацій, тобто миттєвої зміні параметрів

або схеми електричного кола (наприклад, вмиканні чи вимиканні всього кола, або окремих його частин) відбувається перехід з одного усталеного режиму в іншій усталений режим. При цьому виникають зміни струми та напруги, які супроводжуються електромагнітними явищами, що поєднуються терміном "перехідний процес". Перехідні процеси можуть виникати тільки у колах з індуктивними та ємнісними, які можуть накопичувати енергію у вигляді енергії магнітного або електричного поля.

З урахуванням того, що накопичена енергія не може змінитися, то індуктивні та ємнісні елементи мають електромагнітну інерційність, яка враховується за допомогою двох законів комутації.

Перший закон комутації. В індуктивному елементі струм (та магнітний потік) не може змінитися стрибком, тобто безпосередньо після комутації зберігає значення, яке він мав безпосередньо до комутації

iL( 0+ ) = iL = iL( 0− ) ,

(10.1)

ФL( 0+ ) = ФL = ФL( 0− ) ,

Другий закон комутації. На ємнісному елементі напруга (та заряд) не може змінитися стрибком, тобто безпосередньо після комутації зберігає значення, яке вона мала безпосередньо до комутації

uC( 0+ ) = uC = uC( 0− ) ,

(10.2)

q( 0+ )= qC = qC( 0− ) .

PDF created with pdfFactory Pro trial version www.pdffactory.com

79

Перехідні струми та напруги визначаються шляхом вирішення систем інтегро-диференційних рівнянь, що складені за допомогою методу безпосереднього застосування законів Кірхгофа або методу контурних струмів.

10.1.2 Вмикання котушки індуктивності до джерела постійної ЕРС

Розглянемо електричне коло з резистором та котушкою індуктивності схема якого наведена на рис. 10.1.

Рисунок 10.1 – Схема електричного кола з резистором та котушкою індуктивності

До комутації струм у електричному колі (у тому числі й у котушці індуктивності був відсутній), тому що ключ Q був розімкнутий i(0− ) = 0 .

У результаті комутації ключ Q замкнувся й утворився контур. Складемо для нього рівняння за другом законом Кірхгофа

uR + uL = E (10.3)

або виразивши напруги через струм i

PDF created with pdfFactory Pro trial version www.pdffactory.com

80

ЕРС постійна, тому усталений струм буде також постійний. Тоді

де А – постійна інтегрування, е – основа натурального логарифма, р – корінь характеристичного рівняння.

ном комутації безпосередньо після замикання ключа в вітці з індуктивним елементом струм зберігає значення

PDF created with pdfFactory Pro trial version www.pdffactory.com

81

uR (0+ ) = Ri( 0+ ) = 0

З перебігом часу ЕРС самоіндукції убуває, а спад напруги на резистивному елементі (і струм у електричному колі) зростає за аперіодичним законом, асимптотично наближаючись до усталеного значен-

ня (рис. 10.2, а, б).

Рисунок 10.2 – Графіки зміни миттєвих значень струму та напруг у колі з резистивним й індуктивним елементами

PDF created with pdfFactory Pro trial version www.pdffactory.com

83

10.2Порядок проведення підготовчої роботи

10.2.1Вивчити теоретичний матеріал і підготувати усні відповіді на контрольні запитання.

10.2.2Підготувати бланк звіту, до якого повинні входити мета роботи, схема електричного кола (рис. 10.3), таблиця 10.2 та розраху-

нок за п. 10.2.3.

10.2.3Розрахувати перехідний струм та напругу на індуктивному елементі у електричному колі (рис. 10.1), якщо задано: E = 10 Ом,

R = 100 + 10n , L = 0.01n Гн, де n - номер варіанту згідно з журналом групи. Побудувати графіки залежностей i = f ( t ) , uL = f ( t ).

10.3 Опис лабораторної установки

Для виконання лабораторної роботи на стенді використовуються: - генератор прямокутних імпульсів (ГПІ) з внутрішнім опором

Rвн = 51 Ом, який вмикають тумблером S4 ;

- постійний резистор R14 = 120 Ом;

- котушки індуктивності L1 та L2 ; - осцилограф.

10.4 Порядок проведення роботи

10.4.1Увімкнути осцилограф, дати йому прогрітися, встановити межи вимірювань на вісі Y (розгортка амплітуди) - 2 В/поділку, на вісі X (розгортка часу) – 2 мс/поділку, їхні ручки повільного регулювання вивести до упору по годинній стрілці.

10.4.2Вхід осцилографа підімкнути на вихід генератора прямокутних імпульсів, увімкнути тумблер S4 . На його екрані з'явиться рухомий імпульс, який потрібно зупинити. Для цього потрібно ручки осцилографа стабілізації "СТАБ" та рівня "УРОВЕНЬ" повернути проти годинної стрілки до упору, потім повернути ручку "СТАБ" за годинною стрілкою до появлення зображення імпульсу на екрані і повільно зворотним рухом повертаємо ручку до зникнення зображення імпульсу. Після цього повернути ручку "УРОВЕНЬ" за годинною стрілкою до появлення стабілізованого зображення імпульсу на екрані. Замалювати у масштабі

зекрана осцилографа графік зміни напруги на затискачах ГПІ u( t ). З

графіка визначити амплітуду напруги Um . Вимкнути тумблер S4 .

PDF created with pdfFactory Pro trial version www.pdffactory.com

84

10.4.3 Скласти електричне коло за схемою рис. 10.3. Запросити викладача для перевірки правильності складання електричного кола.

Rвн

Рисунок 10.3 - Схема досліджуваного електричного кола з резистором та котушкою індуктивності

10.4.4 Вхід осцилографа підмикнути до резистора R14 , тумблером S4 увімкнути ГПІ. Замалювати у масштабі з екрана осцилографа графік зміни напруги на затискачах резистора R14 uR14 ( t ). З графі-

ка визначити амплітуду напруги Um та усталену складову напруги u y . Результати вимірів записати в таблицю 10.2.

Таблиця 10.2 - Результати дослідження перехідного процесу

10.4.5 Вхід осцилографа підімкнути до котушки індуктивності L1 . Замалювати у масштабі з екрана осцилографа графік зміни напруги на затискачах котушки індуктивності L1 uk ( t ) . З графіка визначити

PDF created with pdfFactory Pro trial version www.pdffactory.com

85

амплітуду напруги Um та усталену складову напруги u y . Результати вимірів записати в таблицю 10.2. Тумблером S4 вимкнути ГПІ.

10.4.6Підімкнутити послідовно з котушкою індуктивності L1 котушку індуктивності L2 . Запросити викладача для перевірки правильності складання електричного кола.

10.4.7Вхід осцилографа підімкнути до резистора R14 , тумблером S4 увімкнути ГПІ. Замалювати у масштабі з екрана осцилографа

графік зміни напруги на затискачах резистора R14 uR14 ( t ). З графіка визначити амплітуду напруги Um та усталену складову напруги

uy . Результати вимірів записати в таблицю 10.2.

10.4.8Вхід осцилографа підімкнути до двох котушок індуктивності L1 та L2 . Ці дві котушки індуктивності вважати за одну. Замалювати у масштабі з екрана осцилографа графік зміни напруги на за-

тискачах двох котушок індуктивності L1 та L2 uk ( t ) . З графіка визначити амплітуду напруги Um та усталену складову напруги u y . Результати вимірів записати в таблицю 10.2.

10.4.9Тумблером S4 вимкнути ГПІ. Результати вимірювань показати викладачеві. Вимкнути осцилограф. Електричне коло розібрати.

10.5Обробка результатів вимірювань та оформлення звіту

10.5.1За графіками зміни напруг для кожного з дослідів визначити сталу часу τ . Для цього потрібно провести дотичну до відповід-

ної кривої в точці, що відповідає моменту часу t = 0 та продовжити її до перетинання з графіком, що відповідає усталеній складовій напруги

uy в точці t = τ . Результати занести в таблицю 10.2.

10.5.2Записати в алгебраїчній формі перехідні функції зміни напруги на затискачах резистора R14 за результатами дослідів 10.4.4 та 10.4.7 та занести їх в таблицю 10.2

10.5.3 Записати в алгебраїчній формі перехідні функції зміни напруги на затискачах котушок індуктивності L1 та L2 uk ( t ) за ре-

PDF created with pdfFactory Pro trial version www.pdffactory.com

86

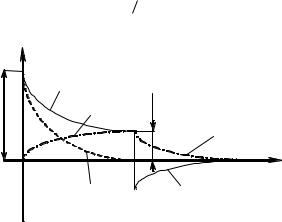
зультатами дослідів 10.4.5 та 10.4.8. Ці функції містять у собі функції

де uRk ( t ) = u y ( 1 - e−tτ ) - активна складова зміни напруги на ко-

Рисунок 10.4 – Графіки зміни напруги на котушці індуктивності та її складових

10.5.4 Розрахувати активний опір котушки індуктивності Rk та занести його в таблицю 10.2. Врахувати, що активний опір котушки

10.5.7 Зробити висновки по роботі.

PDF created with pdfFactory Pro trial version www.pdffactory.com