
лекции ММ ОМД
.pdf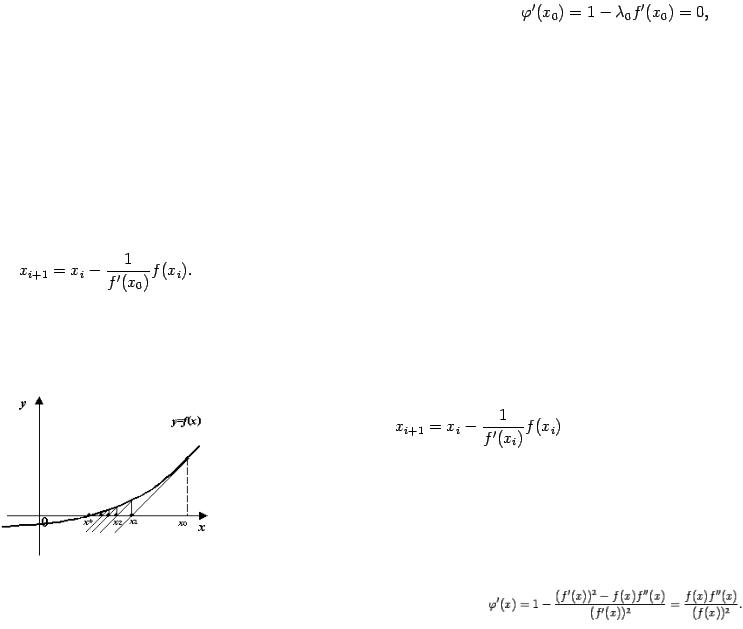
Заметим, что в методе секущих удобно можно фиксировать наиболее удобное для первого шага значение
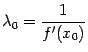 , при котором все секущие параллельны касательной, проведѐнной к графику
, при котором все секущие параллельны касательной, проведѐнной к графику 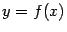 при
при 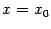 .
.
При таком выборе 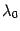 метод секущих называется методом одной касательной. Формула итераций этого метода имеет вид
метод секущих называется методом одной касательной. Формула итераций этого метода имеет вид
Как видно из этой формулы, производную придѐтся вычислить только один раз, а затем на каждом шаге использовать значение
 или, что то же,
или, что то же, 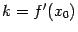 .
.
Рис..Итерации метода одной касательной
При таком выборе 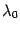 в точке
в точке 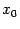 выполнено равенство
выполнено равенство
21
и если отрезок, на котором отделѐн корень и выбрано начальное приближение 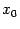 , достаточно мал, а производная
, достаточно мал, а производная 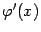 непрерывна, то значение
непрерывна, то значение 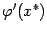 будет не сильно отличаться от
будет не сильно отличаться от 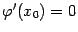 и, следовательно, график
и, следовательно, график 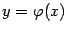 будет пересекать
будет пересекать
прямую 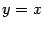 , идя почти горизонтально. А это, как мы отмечали выше, будет давать нам быстрое приближение итераций к корню
, идя почти горизонтально. А это, как мы отмечали выше, будет давать нам быстрое приближение итераций к корню
(так как число  при этом можно выбрать равным
при этом можно выбрать равным  , а эта величина мала).
, а эта величина мала).
33. Метод Ньютона (метод касательных)
Можно предположить, что итерации станут приближаться к корню быстрее, если мы будем выбирать касательную вместо секущей не только на первом, а на каждом шаге. Ясно, что тогда формула итераций будет иметь вид
(1)
Этот метод называется методом касательных, или методом Ньютона. Последовательные приближения метода Ньютона сходятся гораздо быстрее, чем в общем методе итераций .
Поскольку для метода Ньютона
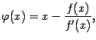 то
то
В точке 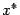 получаем
получаем 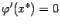 , так как
, так как 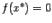 . Тем самым, в
. Тем самым, в
этом методе график 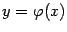 пересекает прямую
пересекает прямую 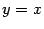 в точности по горизонтали, что приводит к очень быстрой сходимости итераций к
в точности по горизонтали, что приводит к очень быстрой сходимости итераций к 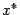 . Именно, имеет место оценка
. Именно, имеет место оценка
2)
где 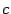 -- некоторая постоянная (не зависящая от
-- некоторая постоянная (не зависящая от 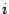 ). Если начальное приближение
). Если начальное приближение 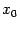 взято достаточно близко от корня
взято достаточно близко от корня 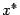 ,
,
то можно взять 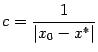 .
.
Скорость сходимости итераций, которая задаѐтся формулой (9.2), называется квадратичной. Квадратичная скорость сходимости означает, примерно говоря, что число
верных знаков в приближѐнном значении 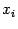 удваивается с каждой итерацией. Действительно, если
удваивается с каждой итерацией. Действительно, если 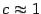 , и
, и
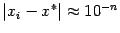 , то
, то 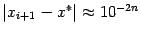 . Это и означает, что число верных знаков при переходе к следующему приближению возросло с
. Это и означает, что число верных знаков при переходе к следующему приближению возросло с 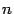 до
до 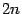 , то есть удвоилось.
, то есть удвоилось.
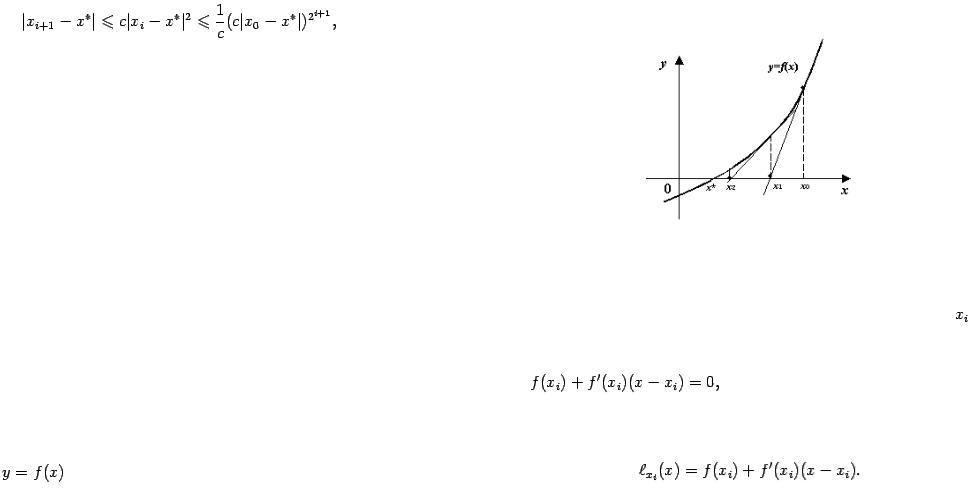
Геометрический смысл метода Ньютона состоит в том, что на каждом шаге мы строим касательную к графику
в |
точке |
очередного |
последовательного |
приближения 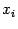 , а за следующее приближение
, а за следующее приближение 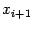 берѐм
берѐм
22
точку пересечения этой касательной с осью 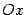 . Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).
. Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).
Рис.. Последовательные приближения метода Ньютона
По-другому идею метода Ньютона мы можем описать так:
на каждом шаге вместо исходного уравнения 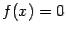 мы
мы
решаем приближѐнное, линеаризованное в точке уравнение
в котором левая часть -- это многочлен Тейлора первого порядка для функции  в точке
в точке 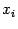 , то есть линейная функция
, то есть линейная функция

|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
Тогда из последнего уравнения сразу определяем |
|
|
||||
Решением |
линеаризованного |
|
уравнения |
|
служит |
|
|
|
|
|
|
|
|
следующее |
приближение |
, |
в то время |
как |
решением |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Подставляя его в предпоследнее уравнение, находим |
|
|
||||
исходного точного уравнения |
|
служит искомый корень |
|
|
|
|
|
|
|
||||
. |
|
|
|
|
|
|
и т. д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Общие формулы имеют вид |
|
|
|
|
||
34 Метод Гаусса решения систем линейных алгебраических |
|
|
|
|
|
|
|
||||||
уравнений.Обратный ход |
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим задачу решения системы уравнений вида: |
|
|
|
|
, k=n, n-1,..., 1. |
(3) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
При вычислениях по формулам (3) потребуется выполнить |
||||||
( |
|
|
|
) |
|
(1) |
примерно 1/2n2 арифметических действий. |
|
|
|
|||
или |
, где |
- матрица |
коэффициентов |
системы, - |
35 |
Метод |
Гаусса |
решения |
систем |
линейных |
|||
вектор неизвестных, - вектор правых частей. |
|
|
|||||||||||
|
|
алгебраических уравнений. Прямой ход |
|
|
|
||||||||
Известно, что система (1) имеет единственное решение, если ее |
|
|
|
||||||||||
матрица невырожденная (т. е. определитель матрицы |
отличен от |
|
|
|
|
|
|
|
|||||
нуля). |
( |
) (1) |
|
|
Известно, что решение системы линейных уравнений можно |
|
|
||
|
|
|
|
|
выразить по формулам Крамера через отношение определителей. |
|
|
|
|
Но вычисление определителя не проще, чем решение исходной |
Приведение системы |
(1) |
к виду (2) |
можно выполнить, |
|
|
|
|
|
системы. Для решения системы порядка n необходимо вычислить |
последовательно заменяя строки матрицы системы их линейными |
|||
|
|
|
|
|
(n+1) определитель, т. е. вычисление решения по формулам |
комбинациями. |
|
|
|
|
|
|
|
|
Крамера в (n+1) раз более трудоемко, чем решение системы |
|
|
|
|
другим методом, например методом Гаусса. |
|
|
|
|
Метод Гаусса основан на приведении путем эквивалентных |
|
|
|
|
преобразований исходной системы (1) к виду с верхней |
|
|
|
|
треугольной матрицей. |
|
|
|
|
|
|
|
(2) |
|
|
Первое уравнение не меняется. Вычтем из второго уравнения |
|||
|
системы (1) первое, умноженное на такое число, чтобы обратился |
|||
|
в нуль коэффициент при |
. |
Затем таким |
же образом вычтем |
(2)первое уравнение из третьего, четвертого и т. д. Тогда исключатся

все коэффициенты первого столбца, лежащие ниже главной диагонали.
Затем при помощи второго уравнения исключим из третьего, четвертого и т. д. уравнений коэффициенты второго столбца. Последовательно продолжая этот процесс, исключим из матрицы все коэффициенты, лежащие ниже главной диагонали.
Запишем общие формулы процесса. Пусть проведено исключение коэффициентов из k-1 столбца. Тогда остались такие уравнения с ненулевыми элементами ниже главной диагонали:
(3)
Умножим k-ю строку на число
(4)
и вычтем из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам
(5)
Производя вычисления по этим формулам при всех указанных индексах, исключим элементы k-го столбца. Будем называть такое исключение циклом процесса. Выполнение всех циклов называется прямым ходом исключения.
Исключение по формулам (4) нельзя проводить, если в ходе
расчета на главной диагонали оказался нулевой элемент 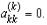 Но в первом столбце промежуточной системы (3) все элементы не могут быть нулями: это означало бы, что det A = 0. Перестановкой строк можно переместить ненулевой элемент на главную диагональ и продолжить расчет.
Но в первом столбце промежуточной системы (3) все элементы не могут быть нулями: это означало бы, что det A = 0. Перестановкой строк можно переместить ненулевой элемент на главную диагональ и продолжить расчет.
Для уменьшения вычислительной погрешности можно каждое повторение внешнего цикла начинать с выбора максимального по
24
модулю элемента в k-том столбце (главного элемента) и перестановки уравнения с главным элементом так, чтобы он оказался на главной диагонали. Этот вариант называется методом Гаусса с выбором главного элемента.
В качестве одной из характеристик эффективности того или иного алгоритма используют вычислительные затраты, измеряемые количеством элементарных операций, которые необходимо выполнить для получения решения.
Для прямого хода метода Гаусса число арифметических операций, в соответствии с формулами (15), (16), равно
Q1 n 2
2 3
3 n3 3
n3 3 2
2  n 2 13
n 2 13 6
6  n
n
Метод Гаусса применим для решения любых систем линейных уравнений, так как он позволяет получить решение системы, если оно существует (включая случай, когда часть неизвестных является свободной и решений бесконечно много) и обнаружить отсутствие решения (когда система несовместна). В последнем случае после очередного k-го шага прямого хода обнаруживается ситуация, когда все элементы матрицы системы ниже k-ой строки равны нулю, а среди соответствующих компонент вектора b есть ненулевые значения.
36 Итерационные методы решения систем линейных алгебраических уравнений . Общая схема
(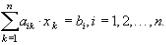 ) (1)
) (1)
Рассмотрим общее описание метода итераций для системы линейных алгебраических уравнений с квадратной матрицей В этом случае по некоторому алгоритму, начиная с выбранного
вектора 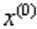 строится последовательность векторов
строится последовательность векторов 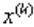 .
.
При этом |
вектор |
выражается через |
известные |
предыдущие |
вектора |
Если |
при |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
Естественно требовать, чтобы объем вычислений для решения |
|||||||||||||
вычислении |
используется |
только |
вектор |
, то |
системы (5) был меньше, чем объем вычислений для исходной |
|||||||||||||||
итерационный метод называется одношаговым (или двухслойным) |
системы (1). |
|
|
|
|
|
|
|
|
|
|
|||||||||
методом. |
|
|
|
|
|
|
36 Точность и сходимость итерационных методов решения |
|||||||||||||
Общий вид линейного одношагового метода |
|
|
систем линейных алгебраических уравнений |
|
|
|||||||||||||||
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
Важную роль играет запись итерационных методов в единой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(канонической) форме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Она имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
||
|
|
|
|
|
|
|
Точность |
метода |
(1,2) |
|
характеризуется |
величиной |
||||||||
|
|
|
|
|
, |
(3) |
погрешности |
|
|
|
, т.е. разностью между решением |
|||||||||
где A - матрица исходной системы уравнений (1), |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- некоторая последовательность невырожденных матриц, |
уравнения |
|
(2) |
и |
точным |
решением |
исходной |
системы |
||||||||||||
линейных алгебраических уравнений. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
- итерационные параметры, |
|
|
Говорят, |
|
что |
итерационный |
метод |
сходится, |
если |
|
|||||||||
Связь между записью итерационного метода в виде (2) и в виде |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(3) выражается формулами: |
|
|
|
|
|
при |
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
В случае, |
когда |
и |
( |
и |
- соответственно) не зависят от |
||||||||
Выбирая различным образом |
и |
, можно получить разные |
номера итерации k, итерационный метод называется |
|||||||||||||||||
варианты итерационных методов, которые различаются скоростью |
стационарным (иначе - нестационарным). |
|
|
|||||||||||||||||
сходимости, сложностью реализации. |
|
|
|
|
Для стационарного линейного одношагового итерационного |
|||||||||||||||
Если |
- единичная |
матрица, |
то |
метод |
называют |
метода |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
явным: |
находится по явной формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(4) |
метод |
(3) |
сходится |
для |
любого |
начального приближения |
||||||||
|
|
|
|
|
|
тогда |
и только |
тогда, когда все |
собственные числа |
матрицы |
||||||||||
В общем |
случае, при |
, |
метод |
называют |
неявным |
|||||||||||||||
перехода S по модулю меньше единицы. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
итерационным |
методом: для |
определения |
надо решать |
В качестве следствия можно получить легко проверяемые на |
||||||||||||||||
систему уравнений |
|
|
|
|
|
практике достаточные условия. Норма матрицы S, согласованная с |
||||||||||||||
|
|
|
|
|
|
(5) |
векторной |
нормой |
удовлетворяет |
неравенству |
|
для |
||||||||
|
|
|
|
|
|
|
любого вектора x. Примерами легко вычисляемых согласованных |
|||||||||||||
|
|
|
|
|
|
|
норм являются: |
|
|
|
|
|
|
|
|
|
||||
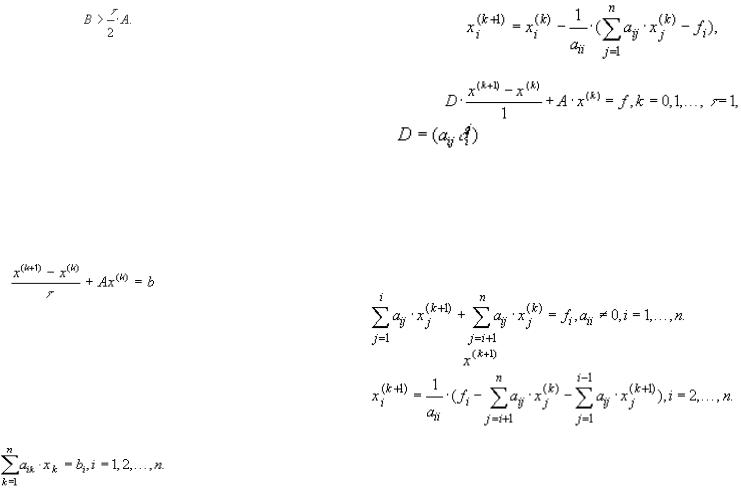
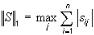 ,
,  .
.
Таким образом, выполнение любого из неравенств 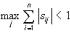
, 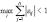 достаточно для сходимости итерационного метода. Достаточные условия сходимости для итерационного метода,
достаточно для сходимости итерационного метода. Достаточные условия сходимости для итерационного метода,
записанного в канонической форме (2) , имеют вид:
(4)
Тогда метод итераций
Напомним, что матрица положительная, если для любого ненулевого вектора x (Ax,x)>0.
37. Варианты итерационных методов. Методы простых итераций и Якоби
Метод простых итераций
В качестве первого примера рассмотрим явный стационарный итерационный метод, каноническая форма которого:
Метод Якоби
Координатная форма записи этого варианта итерационного метода имеет вид:
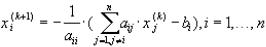 .
.
Эти формулы получаются непосредственно из исходной системы:
26
если i - ое уравнение системы разрешить относительно
неизвестного 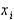 . Подставляя сюда
. Подставляя сюда
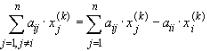 ,
,
получаем
или, в каноническом виде,
где |
- диагональная матрица. |
|
||
Сходимость |
этого |
метода |
гарантирована, |
если |
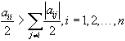 .
.
38. Варианты итерационных методов. Методы Зейделя и релаксации.
Весьма широко на практике применяется итерационный метод Зейделя:
Компоненты |
находятся последовательно по формулам: |
Запишем этот метод в матричной форме. Для этого представим матрицу A в виде суммы
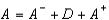 ,
,
где

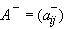 ,
, 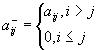 - нижняя треугольная матрица,
- нижняя треугольная матрица,
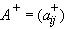 ,
, 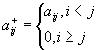 - верхняя треугольная матрица.
- верхняя треугольная матрица.
В этих обозначениях метод Зейделя записывается следующим образом:
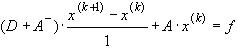 (28)
(28)
Применим теорему 2 для исследования сходимости метода Зейделя.
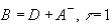 . В этом случае
. В этом случае
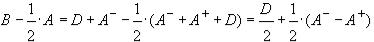 ,
,
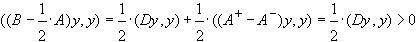 ,
,
если 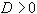 . Следовательно, метод Зейделя сходится, если
. Следовательно, метод Зейделя сходится, если 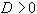 . Неравенство
. Неравенство 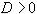 следует из условия
следует из условия 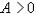 .
.
Таким образом, метод Зейделя всегда сходится, если A - положительная матрица.
Метод релаксации
Можно ускорить сходимость метода Зейделя, если ввести итерационный параметр (параметр релаксации) 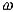 .Получим
.Получим
.
Значение 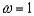 соответствует методу Зейделя.
соответствует методу Зейделя.
39. Классификация дифференциальных уравнений в частных производных.
Приближенные методы решения наиболее разработаны для диф-
27
ференциальных уравнений в частных производных второго порядка с двумя независимыми переменными. Для решения многих практических задач необходимо рассматривать так называемые линейные или вполне линейные дифференциальные уравнения в частных производных, т. е. дифференциальные уравнения первой степени относительно искомой функции и всех ее производных и не содержащие их произведений. Такие уравнения можно представить в следующем виде:
В уравнении (1) искомой является функция z, а х и у — независи-
мые переменные. Функции А (х, у), В (х, у), С (х, у}, а(х, у), b(х, у}, с (х, у) — непрерывные функции от х и у, имеющие непрерывные частные производные.
Проведем классификацию дифференциальных уравнений в частных производных, основанную на рассмотрении уравнения
(1). Введем обозначения
(для удобства записи частных производных «штрихи» опускаются) и рассмотрим упрощенную форму уравнения (I):
соответствующую (1) при a b c F 0 .
Уравнение (2) всегда может быть приведено к одной из трех стандартных канонических форм. Этими формами являются эллиптические, параболические и гиперболические дифференциальные уравнения в частных производных. Тип уравнения определяется значением коэффициентов в выражении
(2) и связан со знаком дискриминанта
B 2 x , y  4A x , y C x , y
4A x , y C x , y 
в выражении (2).
В зависимости от знака дискриминанта имеем:
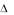 0 — эллиптический тип в точке (х, у);
0 — эллиптический тип в точке (х, у);

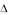 0 — параболический тип в точке (х, у);
0 — параболический тип в точке (х, у);
0 — гиперболический тип в точке (х, у).
Если коэффициенты A, В и С постоянные, не зависящие от х и у, то канонические уравнения являются полностью эллиптическими, параболическими или гиперболическими.
40. Дифференциальные уравнения эллиптического, параболического и гиперболического типа.
Чтобы показать, как строятся канонические дифференциальные уравнения в частных производных, рассмотрим выражение (2) с постоянными А, В и С. Введем две новые переменные
где
Поскольку уравнение (2) линейное относительно производных искомой функции z(х,у), то решение z(х, у) этого уравнения может быть представлено в форме
Рассмотрим функцию z(х,у) как функцию z ,
,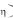 двух новых переменных
двух новых переменных 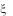 и . Тогда, учитывая замену переменных (3) и вид
и . Тогда, учитывая замену переменных (3) и вид
искомой функции (4), получим для частных производных следующие выражения:
Используя найденные значения производных, представим уравнение (2) в виде
Рассмотрим уравнение
оно имеет два корня а1 и а2 , которые могут быть действительными
28
и различными, действительными и равными или комплексно
сопряженными. Тип корней зависит от величины дискриминанта В2 — 4АС.
В случае В2 — 4АС >0 корни а1 и а2 уравнения (6) действительны
и различны, причем коэффициенты первого и третьего членов выражения (5) равны нулю. При этом равенство (5) имеет вид
канонической формы гиперболического дифференциального уравнения в частных производных
или
соответствующей выражению (1).
Перейдем к построению канонической формы дифференциального уравнения эллиптического типа. Если В2 — 4АС = 0, то оба корня
а1 и а2 уравнения (6) — действительные числа и переменные 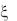 и являются зависимыми. Положим один из корней равным
и являются зависимыми. Положим один из корней равным
а |
1 |
В , тогда а2 может быть произвольным, причем а1 а2 . |
|
2А |
|||
|
|
Подставляя а1 и а2 в соотношение (5), получим
Выражение (8) является канонической формой параболического дифференциального уравнения в частных производных. В общем случае его можно записать в виде
Если В2 — 4АС < 0, то а1 и а2 являются комплексно сопряженными:
а1 b1 ib2 и а2 b1 ib2 . Тогда равенство (5) принимает вид
Выражение (9) является канонической формой дифференциального уравнения эллиптического типа. В общем случае уравнение (9)
можно записать так:

Классическими примерами дифференциальных уравнений в частных производных являются уравнение Лапласа
(имеющее каноническую эллиптическую форму),
уравнение теплопроводности
(имеющее каноническую параболическую форму) и
волновое уравнение
(имеющее каноническую гиперболическую форму).
41. Конечно-разностные аппроксимации.
Конечно-разностные аппроксимации для частных производных являются наиболее распространенным подходом к численному интегрированию дифференциальных уравнений в частных производных.
Частные производные заменяются соответствующими разностными соотношениями по соответствующим независимым переменным. В общем случае размерность области, в которой необходимо найти решение дифференциального уравнения в частных производных, равна числу независимых переменных. В случае двух независимых переменных х и у область является двумерной.
29
Метод, используемый для конечно-разностной аппроксимации, основывается на покрытии области сетью прямоугольных клеток шириной h (в направлении оси Ох) и высотой k (в направлении оси Оу}. Величина зависимой переменной z=z(x,y) устанавливается в любой точке в пределах области. В частности, когда задана одна точка прямоугольной сети с координатами x r , y s , окружающие ее
четыре точки имеют координаты
x r h ,ys ; x r h ,ys ; x r ,ys h ; x r ,ys h . Геометрический способ покрытия области сеткой показан на рис. 10.1, Введем следующие операторы: Е — оператор приращения; 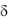 —
—
оператор центральных разностей; — разностный оператор опережения; D — дифференциальный оператор.
Эти операторы определяются следующими соотношениями:
Представим f(х + h) в виде разложения в ряд Тейлора:
Используя оператор D, представим оператор Е в виде
или, пользуясь разложением экспоненциальной функции ehD в ряд Тейлора, преобразуем выражение (6) так:
Тогда зависимость оператора Е от D может быть представлена в форме
или
Из выражений (1) и (2) получаем следующее соотношение между операторами Е и :

или
Подставляя выражение (10) в формулу (8), получим
Используя разложение логарифмической функции в ряд:
получим следующее выражение для оператора D:
Распространяя изложенный метод на разности второго порядка, имеем
или
В формулах (13) и (15) можно ограничиться подходящим числом членов, чтобы получить конечно-разностное представление для производной с желаемой точностью. Ограничиваясь в каждом выражении первой и второй разностью для производных:
имеем соответственно
Для наглядного представления уравнений вида (18) и (19) используют шаблоны, имеющие следующий вид:
30
В приведенных шаблонах в центре кругов указываются коэффициенты дифференциального уравнения. Круг центральной части шаблона соответствует величине zr . Положительным
приращениям по горизонтальным линиям (рис. 10.1) соответствует левый конец, отрицательным — правый конец шаблона. Аналогичные шаблоны можно получить и в случае использования
оператора 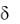 центральных разностей. Полагая в соотношении (6) значения переменной равными х + h/2 и х — h/2, имеем
центральных разностей. Полагая в соотношении (6) значения переменной равными х + h/2 и х — h/2, имеем
поэтому, пользуясь соотношением (4), получаем
или в операторном виде
т. е.
Разлагая гиперболическую функцию arcsh |
2 |
в ряд, имеем |
|
|
Непосредственным возведением в степень получим
Соотношения для производных, выраженных через центральные
