M04700
.pdf31
ущільнень. Як правило, рідинні приладі використовують для вимірювання тисків у діапазоні до 0,5 МПа (інколи до 15 МПа).
Дія механічних приладів базується на зв’язку між тиском, що рідина чине на спеціальний чутливий елемент, та деформацією останнього. Механічні прилади дозволяють вимірювати будь-які тиски (практичний діапазон від 50 Па до 1000 МПа), але точність їх нижча, ніж у рідинних приладів. Властивості матеріалу чутливих елементів з бігом часу змінюються, через це такі прилади потребують періодичного тарування.
3.2.3 Основне рівняння гідростатики
Тиски у двох точках, що розташовані в однорідній рідині у спокої, пов’язані за допомогою основного рівняння гідростатики:
pm = pn ± ρgh , |
(3.3) |
де m та n – позначення точок; ρ – густина рідини, кг / м3;
g– прискорення вільного падіння, м /с2;
h– відстань між точками уздовж вертикалі, м.
У рівнянні (3.3) pm та pn обов’язково є однойменними тисками (обидва абсолютні, або обидва надлишкові). Знак перед другим доданком у формулі (3.3) залежить від взаємного розташування точок: якщо точка m розташована нижче, ніж точка n, то становиться знак «плюс». При зміні взаємного розташування точок змінюється також знак у рівнянні.
Для системи, що складається з різнорідних рідин, розрахункову формулу для визначення тиску одержують послідовним застосуванням рівняння (3.3) для кожної пари точок, що містяться в однорідному середовищі. Методику виведення розрахункових формул для рідинних систем (різних приладів) наведено далі.
3.2.4 Методи вимірювання швидкості потоків
Вимірювання швидкості потоків рідин (газів) ґрунтується на енергетичному балансі в суцільному середовищі: перетворенні кінетичної енергії у потенціальну. В припущенні нестисливості суцільного середовища, що є справедливим для потоків крапельних рідин а також газових потоків, що рухаються з відносно невеликими швидкостями, такий баланс енергій описується рівнянням Д.Бернуллі:
PDF created with pdfFactory Pro trial version www.pdffactory.com
32
|
W |
2 |
|
|
|
W |
2 |
2 |
|
|
|
|
|
p + ρ × |
1 |
|
= p |
2 |
+ ρ × |
|
|
+ Dp |
ς |
, |
(3.4) |
||
|
|
|
|
|
|||||||||
1 |
2 |
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
де індексами «1» та «2» позначено порядковий номер перерізу потоку середовища у напрямку його руху, pζ – втрати тиску, зумовлені вихроутвореннями в локальних областях середовища та розігрівом потоку через дію сил внутрішнього тертя.
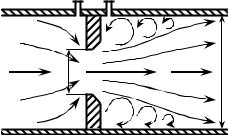
В ідеальному нев’язкому середовищі сума потенціальної енергії сил тиску та кінетичної енергії потоку є величина незмінна у будьякому з його перерізів. Перехід однієї форми механічної енергії в іншу можна спостерігати у вигляді певних фізичних ефектів: обертання турбінки в потоці середовища, зростання тиску під час зупинки потоку, зменшення тиску під час дроселювання (звуження) потоку. Останній спосіб може бути реалізованим за допомогою звичайної діафрагми (рис. 3.1) з отвором діаметром d0 (площею F0), яку встановлено в циліндричному каналі діаметром d (площею F).
p1 
p2
W
d0
W0
d
Рисунок 3.1 – Схема проходження потоку крізь діафрагму
Потік на підході до діафрагми звужується, а після проходження крізь отвір діафрагми – розширюється. Згідно із законом нерозривності потоку у звуженому перерізі підвищується швидкість потоку W0 в порівнянні з його швидкістю W до звуження. На основі закону збереження та перетворення енергії збільшення швидкості потоку і, як наслідок, збільшення кінетичної енергії у звуженому перерізі, – викликає зменшення потенціальної енергії потоку в цьому перерізі. Відповідно, статичний тиск у звуженому перерізі (p2) буде меншим, ніж у перерізі до діафрагми (p1).
PDF created with pdfFactory Pro trial version www.pdffactory.com
33
Таким чином, при протіканні суцільного середовища крізь діафрагму створюється перепад тиску, який залежить від швидкості потоку W та геометрії діафрагми. Тому на підставі формули (3.4) можна одержати формулу для розрахунку швидкості потоку у вигляді:
W = ϕ × |
|
, |
(3.5) |
2 ×(p1 - p2 ) ρ |
де φ – коефіцієнт швидкості, який враховує втрати механічної енергії.
3.2.5 Критерії гідрогазодинамічної подібності
Виділити фізичні величини, що підлягають експериментальному визначенню, дозволяє перша теорема подібності, згідно якої подібними процесами (явищами) вважають такі, що мають ідентичні відповідні числа (критерії) подібності.
Коли йдеться про подібність процесів руху суцільних середовищ, то частіше за все користуються такими критеріями:
– число Рейнольдса – характеризує співвідношення сил інерції
та сил внутрішнього тертя: |
Re = W × L ν ; |
(3.6) |
– число Фруда – характеризує співвідношення сил інерції та сил |
||
ваги: |
Fr = W 2 (g × L); |
(3.7) |
– число Ейлера – характеризує співвідношення сил тиску та сил |
||
інерції: |
Eu = p (ρ ×W 2 ); |
(3.8) |
– число Лагранжа – характеризує співвідношення сил тиску та сил внутрішнього тертя: La = Re× Eu = (L × p)
(μ ×W ). (3.9)
Якщо досліджують нестаціонарні процеси руху суцільних середовищ, то використовують критерій гідрогазодинамічної гомохронності (число Струхаля): Ho = W ×τ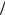
L . (3.10)
3.3 Завдання на підготовку до лабораторної роботи
Перед тим як стати до лабораторної роботи, студентам необхідно засвоїти теоретичний матеріал розділів “Основи механіки рідин та газів” та “Основи теорії подібності”. Слід приділити особливу увагу з’ясуванню фізичної суті основного рівняння гідростатики та чітко уявляти фізику процесу перетворення енергії в потоці суцільного середовища, а також основні ознаки подібності процесів та явищ.
PDF created with pdfFactory Pro trial version www.pdffactory.com
34
В процесі підготовки до лабораторної роботи слід користуватися літературою [1–4], конспектом лекцій, а також даними методичними вказівками.
До початку лабораторної роботи слід також підготувати ілюстративні матеріали, згідно з вимогами розділу 3.7 даних методичних вказівок.
3.4 Контрольні запитання для самоперевірки і контролю підготовленості студентів до роботи
1.Визначення тисків: атмосферного, надлишкового, абсолютного, вакууму, та зв’язок між ними.
2.Одиниці вимірювання тисків, їх класифікація.
3.Основне рівняння гідростатики, його фізична суть (розуміння) та практичне застосування.
4.Розрахункові формули для визначення тиску (чи різниці тисків) у випадку багато рідинних систем.
5.Основні типи приладів, їх позитивні якості, недоліки та галузь застосування.
6.Енергетичний баланс в потоці суцільного середовища.
7.Принципи вимірювання швидкості потоків середовища.
8.Фізична суть критеріїв Рейнольдса, Фруда, Ейлера, Лагранжа, Струхаля.
3.5 Матеріали, інструмент, прилади, обладнання
Найпростішим приладом для вимірювання надлишкового тиску є п’єзометр (рис. 3.2). Він являє собою трубку, один кінець якої з’єднується з резервуаром, а другий – відкритий у атмосферу.
Для вимірювання додатного надлишкового (манометричного) тиску п’єзометр установлюють згідно зі схемою, наведеною на рисунку 3.2.а. Тоді тиск у заданій точці m розраховують за формулою
pm = ρ × g × h . |
(3.11) |
Для вимірювання вакуумметричного тиску |
п’єзометр |
установлюють згідно зі схемою, наведеною на рисунку 3.2.б. Тоді тиск у заданій точці m розраховують за формулою
pm = - ρ × g × h . |
(3.12) |
PDF created with pdfFactory Pro trial version www.pdffactory.com
35
а)
ρ
h
0 m
0
0 m |
0 |
|
h |
|
ρ |
б) |
|
а) – для манометричних тисків; б) – для вакуумметричних тисків
Рисунок 3.2 – П’єзометр
1
h1
0 m
0
2 |
|
ρ1 |
|
h |
|
||
|
|
2 |
|
|
|
|
|
ρ2
Рисунок 3.3 – U-подібний манометр
Для вимірювання як манометричного, так і вакуумметричного надлишкового тиску застосовують U-подібний манометр (вакуумметр), схему якого показано на рисунку 3.3. Спільне розв’язання рівнянь рівноваги рідин на межах розподілу рідин (в точках 1 та 2) дозволяють визначити тиск у заданій точці m за формулою (3.13):
pm = ρ1 × g × (h1 + h2 )- ρ2× × g × h2 .(3.13)
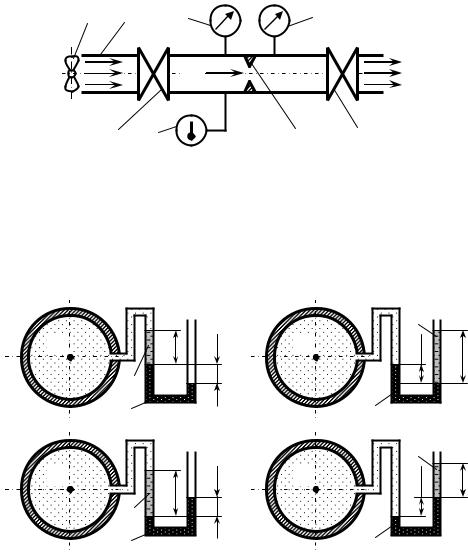
Для вимірювання різниці тисків використовують диференціальні манометри, які виконують за різними схемами: рисунок 3.4.а (для випадку ρ1 > ρ2 < ρ3) та рисунок 3.4.б (для випадку ρ1 < ρ2 > ρ3).
а) |
1 |
ρ3 |
0 |
m |
|
|
h |
ρ2 |
|
|
h |
ρ1 |
|
|
|
|
0 |
|
2 |
|
ρ1 |
2 |
|
|
|
|
|
||
|
|
0 |
|
|
h |
0 m |
|
h |
n 0 |
ρ3 |
|
|
|
1 |
а) – для рідини-посередника незначної густини; б) – для рідини-посередника значної густини.
Рисунок 3.4 – Диференціальний манометр
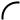n 0
ρ2
б)
PDF created with pdfFactory Pro trial version www.pdffactory.com
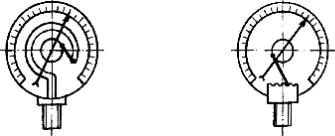
36
Тоді різницю тисків у заданих точках m та n можна розрахувати
за формулою: |
|
D p = pm - pn = (ρ1 - ρ2 )× g × h0 + (ρ1 - ρ3 )× g × h . |
(3.14) |
У розповсюдженому випадку, коли ρ1 = ρ2 (у резервуарах знаходяться однорідні рідини), розрахункову формулу для визначення різниці тисків можна спростити:
D p = (ρ1 - ρ2 )× g × h |
(3.15) |
Більшість механічних приладів тиску призначено для вимірювання надлишкових (вакуумметричних) тисків.
Чутливий елемент механічного приладу тиску може виготовлятися за різними конструктивними схемами. На рисунку 3.8 наведено два варіанти виготовлення чутливого елементу: вигнута трубка (рис. 3.5.а) та мембрана (рис. 3.5.б).
а) б)
а) з вигнутою трубкою; б) з мембраною
Рисунок 3.5 – Механічний манометр (вакуумметр)
Вигнута трубка в манометрі має овальний переріз, який під дією тиску змінює свою форму. Це призводить до розгинання (згинання) трубки і відповідного обертання стрілки. Мембрана механічного манометра може пружно деформуватися під дією тиску, що також призводить до обертання стрілки приладу.
Структурну схему лабораторної установки для дослідження параметрів рухомих середовищ наведено на рисунку 3.6.
Установка являє собою горизонтальний трубопровід 1 з внутрішнім діаметром d = 92 мм, в який з атмосфери нагнітається повітря за допомогою компресора 2 сталої продуктивності. Швидкість повітряного потоку в трубі регулюється за допомогою запірних
PDF created with pdfFactory Pro trial version www.pdffactory.com
37
пристроїв 3 та 4. У трубопровід вмонтовано стандартну діафрагму 5 з діаметром отвору d0 = 58 мм таким чином, щоб довжина труби до і після діафрагми становила від 10-ти до 20-ти значень діаметра d .
2 |
1 |
7 |
|
8 |
|
|
p1 |
p2 |
|
|
|
W |
|
|
|
|
t |
|
|
|
3 |
6 |
5 |
4 |
Рисунок 3.6 – Схема лабораторної установки
Для контролю параметрів повітряного потоку до установки підключено: термометр 6, за допомогою якого контролюють температуру повітря перед діафрагмою, механічний манометр 7 для вимірювання надлишкового тиску перед діафрагмою та рідинний прилад 8 для вимірювання тиску за діафрагмою. Схеми підключення приладів 7 та 8 задаються окремо (рисунки 3.7 та 3.8).
p2 |
h |
h |
p2 |
|
2 |
1 |
|
|
ρ2 |
|
|
а) |
ρ1 |
в) |
|
p2 |
h |
p2 |
|
1 |
|
|
2 |
|
|
h |
|
|
ρ2 |
|
б) |
ρ1 |
г) |
ρ2 |
|
1 |
|
h |
2 |
|
h |
ρ1 |
|
ρ2 |
|
1 |
2 |
h |
h |
ρ1 |
|
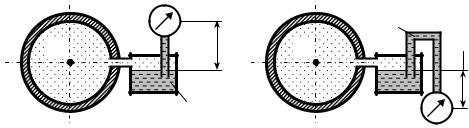
Рисунок 3.7 – Схеми підключення приладу тиску після діафрагми
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
|
38 |
|
|
|
pм |
|
|
ρ |
p1 |
|
|
p1 |
|
h |
|
h |
||
|
|
|
|
|
а) |
ρ |
б) |
|
pм |
|
|
Рисунок 3.8 – Схеми підключення приладу тиску перед діафрагмою
3.6 Порядок виконання лабораторної роботи
Біля експериментальної установки студенти працюють лише під наглядом викладача або лаборанта, суворо дотримуючись вимог інструкції з охорони праці при виконанні робіт в лабораторіях кафедри “Теплотехніка та гідравліка”.
Зафіксувати барометричний тиск p0 та температуру навколишнього середовища t0.
Підключити прилади 7 та 8 за заданою викладачем схемою. Відкрити повністю вентиль 3 на трубопроводі біля компресора,
закривши вентиль 4 у вільного кінця трубопроводу.
Увімкнути електродвигун компресора 2 за допомогою пакетного вимикача. Регулівними пристроями 3 та 4 забезпечити певний стаціонарний режим роботи установки.
Зафіксувати показання приладів тиску.
Точність для вимірювання величин – ціна поділу шкал приладів. Виконати необхідні розрахунки. Оформити звіт.
3.7 Зміст звіту
Вказати тему та мету лабораторної роботи. Записати формули (3.1) – (3.5) з поясненням величин, що в них входять. Зарисувати структурну схему експериментальної установки (рисунок 3.5).
Зарисувати схеми підключення приладів для вимірювання тиску, які було застосовано у дослідах.
Зарисувати форму протоколу (таблиця 3.2).
Занести до протоколу всі величини, визначені з експерименту.
PDF created with pdfFactory Pro trial version www.pdffactory.com
39
Таблиця 3.2 – Форма протоколу (параметри, визначені з досліду)
Назва параметра |
Позначення, |
Числове |
|
розмірність |
значення |
||
|
|||
Барометричний тиск |
p0 , кПа |
|
|
Температура навколишнього середовища |
t0, °С |
|
|
Показання механічного манометра |
pм , кГс/см2 |
|
|
Розташування механічного манометра |
h, м |
|
|
Сорт рідини-посередника |
ρ, кг/м3 |
|
|
Показання рідинного приладу тиску |
h1, мм |
|
|
h2, мм |
|
||
|
|
||
Робочі рідини в приладі |
ρ1, кг/м3 |
|
|
ρ2, кг/м3 |
|
Визначити тиск p1 перед діафрагмою та тиск p2 після неї. Це можна зробити, застосувавши формулу (3.3), користуючись поясненнями п.п. 3.2.3 та прикладами застосування формул (3.11) – (3.15).
Далі необхідно визначити швидкість потоку повітря за формулою (3.5) враховуючи, що значення коефіцієнта швидкості експериментальної діафрагми φ = 0,5787, а значення густини повітря ρ0 розраховується за формулою (3.1), де газова стала для повітря – R = 287 Дж/(кг·К).
Після цього необхідно на основі аналізу критеріїв подібності (див. п.п 3.2.5) зробити висновки про величину характерних параметрів потоку, якщо на тій самій установці моделювати подібний процес руху води (оскільки в діапазоні температур від 4 до 40 °С змінювання густини води не перебільшує 1 %, з достатньою точністю можна прийняти ρводи = 1000 кг/м3). Результати розрахунків слід подати у вигляді таблиці (табл. 3.3).
Таблиця 3.3 – Параметри подібних модельних потоків
|
µ |
ν |
W |
p1(надл) |
p2(надл) |
|
Па·c |
м2/с |
м/с |
Па |
Па |
сухе повітря |
|
|
|
|
|
вода |
|
|
|
|
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
40
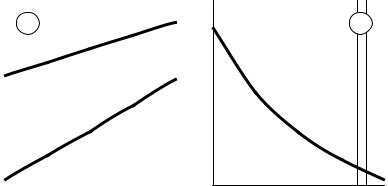
Фізичні характеристики рухомих середовищ, зокрема їх в’язкість (здатність чинити опір відносному зсуванню частинок), суттєво залежать від температури. Для розрахунку критеріїв подібності необхідні значення динамічного µ та кінематичного ν коефіцієнтів в’язкості (µ = ν ·ρ) можна визначити за графічними залежностями, представленими на рисунку 3.9.
коефіцієнтив’язкості |
(с·Па,µν , м |
|
) с / |
|
2 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
·106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
19 |
|
|
|
а |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν ·106 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
ν |
·10 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
µ |
·10 |
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
10 |
|
|
20 |
30 |
|
|
40 |
|
|
|
10 |
|
20 |
|
|
|
|
30 |
40 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
температура t, °C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
а) – для сухого повітря |
|
|
|
|
|
|
|
|
|
|
|
|
б) – для води |
|
|
|
|
|
|||||||||||||||||||||||||||||
Рисунок 3.9 – Температурні залежності коефіцієнтів в’язкості
3.8 Рекомендована література
1.Єгоров Я.О., Бєліков С.Б., Улітенко О.М. Теоретичні основи теплотехніки у системах машинобудування. Запоріжжя:
Дике Поле, 2004. – С. 59 – 72, 178 - 190.
2.Слинько Г.І., Бєліков С.Б., Улітенко О.М. Теплотехнічні процеси та теплова обробка матеріалів і виробів. – Мелітополь: ООО «Издательский дом Мелитопольской городской типографии», 2011. – С. 57 - 80.
3.Сергель О.С. Прикладная гидрогазодинамика. – М.:
Машиностроение, 1981. – с.234 - 256.
4.Петунин А.Н. Измерение параметров газового потока. - М.: Машиностроение, 1974. гл. 1.
PDF created with pdfFactory Pro trial version www.pdffactory.com