
- •Методичні вказівки до лабораторних робіт з фізикИ Оптика
- •1 Лабораторна робота № 61 визначення показника заломлення рідини за допомогою рефрактометра
- •Теоретична частина
- •Опис рефрактометра та методики вимірювання
- •Завдання
- •Контрольні запитання
- •2 Лабораторна робота № 62 дослідження явища інтерференції світла
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •3 Лабораторна робота № 63 дослідження дифракції фраунгофера на щ1лині
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Хід роботи
- •Контрольні запитання
- •Література
- •4 Лабораторна робота № 64 дифракція на дифракційній решітці
- •Теоретична частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •5 Лабораторна робота № 65 дослідження поляризованого св1тла
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •6 Лабораторна робота № 66 перевірка закону стефана-больцмана
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •7 Лабораторна робота № 67 побудова дисперсійної кривої монохроматора ум-2
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •8 Лабораторна робота № 68 дослідження спектру атому водню
- •Теоретична частина
- •Експериментальна частина
- •Хід роботи
- •Контрольні запитання
- •Література
- •Laboratory work № 61 studying the phenomenon of interference
- •Laboratory work n 63
- •Investigation phenomena of polarization of light
- •The short theory
- •Control questions
- •Laboratory work № 65 Study of energy levels of a hydrogen atom
- •A short theory
- •The experimental part
- •Control Questions
Хід роботи
1. Направимо промінь від лазера 1 за допомогою дзеркала 2 через поляроїд 3 на фотодіод 4. При цьому міліамперметр покаже певний

Рисунок 5.4
струм, сила якого залежатиме від інтенсивності світлового потоку.
Будемо повільно обертати поляроїд 3 навколо власної осі у якийсь один бік з метою встановити на міліамперметрі 5 максимальне значення струму. Коли фотострум досягне максимального значення, це означатиме, що площина поляризації лазерного променя співпала з власною площиною поляроїда; при цьому у формулі (5.2) кут
 .
.Повільно обертаючи поляроїд у якийсь один бік, будемо фіксувати значення фотоструму через кожні
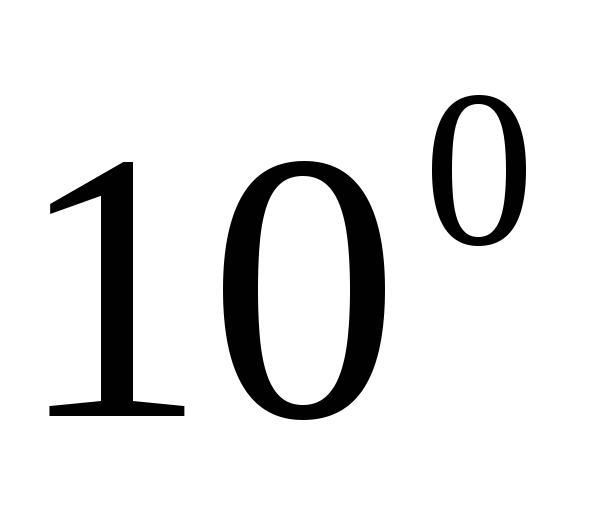 в інтервалі
в інтервалі .
Данні занесемо в таблицю.
.
Данні занесемо в таблицю.Розрахуємо значення
 та
та для відповідних значень
для відповідних значень ,
та побудуємо графік залежності
,
та побудуємо графік залежності від
від .
Згідно закону Малюса інтенсивність
.
Згідно закону Малюса інтенсивність повинна лінійно залежати від
повинна лінійно залежати від .
Оскільки фотострум
.
Оскільки фотострум пропорційний інтенсивності
пропорційний інтенсивності ,
то лінійний характер графіку
підтверджуватиме справедливість закону
Малюса.
,
то лінійний характер графіку
підтверджуватиме справедливість закону
Малюса.
|
|
|
|
|
|
0 |
|
|
|
|
10 |
|
|
|
|
20 |
|
|
|
|
30 |
|
|
|
|
40 |
|
|
|
|
50 |
|
|
|
|
60 |
|
|
|
|
70 |
|
|
|
|
80 |
|
|
|
|
90 |
|
|
|
Зробити висновки щодо справедливості закону Малюса..
Контрольні запитання
Що таке світло з сучасної наукової точки зору?
Як в електромагнітній хвилі орієнтовані один відносно одного вектори
 ?
?Що таке площина поляризації?
Чим поляризоване світло відрізняється від природного?
В чому полягає закон Малюса?.
Література
Ландcберг Г. С. Оптика. – М.: Наука, 1976.
Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.
Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982.
Физический энциклопедический словарь.- М.: СЭ, 1999.
Методичні вказівки розробила доц. Богачьова Л.С.
Рецензент доц. Правда М. І.
6 Лабораторна робота № 66 перевірка закону стефана-больцмана
Мета роботи: Перевірити закон Стефана-Больцмана.
Прилади і обладнання: джерело струму, лампа розжарювання, термостовпчик, міліамперметр.
Теоретична частина
Випромінювання
світла відбувається в результаті
переходів атомів і молекул із станів з
більшою енергією в стани з меншою
енергією. Теплове випромінювання
відрізняється від інших видів
випромінювання (люмінесценції) способом
переходу систем, що випромінюють, у
збуджені стани. При тепловому випромінюванні
такий перехід відбувається за рахунок
теплового руху атомів та молекул.
Інтенсивність теплового випромінювання
характеризується енергетичною світимістю
![]() ,
яка визначається як кількість променевої
енергії, що випромінюється одиницею
поверхні тіла за одиницю часу, тобто:
,
яка визначається як кількість променевої
енергії, що випромінюється одиницею
поверхні тіла за одиницю часу, тобто:
![]() ,
(6.1)
,
(6.1)
де Q – енергія, що випромінюється тілом з площі S за час t.
Теплове випромінювання складається з хвиль різної довжини λ. Доля енергетичної світимості, яка припадає на елементарний інтервал dλ має вигляд:
![]() ,
(6.2)
,
(6.2)
тому енергетична світимість може бути представлена у вигляді:
![]() ,
(6.3)
,
(6.3)
де rλ – емісійна здатність тіла, або густина енергетичної світимості, яка
визначається як:
![]() .
(6.4)
.
(6.4)
Нехай на елементарну площину dS в діапазоні хвиль dλ падає потік променевої енергії dФλ. Частина цього потоку dФ′λ поглинається тілом. Тоді величина:
 (6.5)
(6.5)
називається поглинальною здатністю тіла.
Тіло, що поглинає випромінювання будь-якої довжини хвилі називається абсолютно чорним. Для абсолютно чорного тіла α = 1 для всіх довжин хвиль. Якщо для деякого тіла α < 1 і для всіх довжин хвиль λ стале, то таке тіло називається сірим.
Згідно з законом Стефана-Больцмана енергетична світимість абсолютно чорного тіла:
![]()
![]() ,
(6.6)
,
(6.6)
а для сірого тіла:
![]() ,
(6.7)
,
(6.7)
де Т
– абсолютна температура, а σ
– стала Стефана-Больцмана, яка дорівнює:
σ
5,6710–
8
![]() ,
а величинаα
< 1, має назву коефіцієнта чорноти.
,
а величинаα
< 1, має назву коефіцієнта чорноти.
