3.5.2 Теорема Барбашина-Красовского
Теорема Ляпунова
требует, чтобы в течение всего переходного
процесса было
(рис. 1а). Очевидно, что в случае,
изображенном на рис. 1б, система также
будет асимптотически устойчивой.Теорема
Барбашина-Красовского охватывает и
этот случай.
Рассматривается система (3.5.1.1).
Теорема.
Если для
системы (3.5.1.1) в области
существуетопределённо
положительная функция
,
такая, что её полная производная по
времени, взятая в силу системы (3.5.1.1),
будетзнакоотрицательной
(
),
причём множество точек, где
,
не содержит целых траекторий кроме
начала координат, то положение равновесия
будет асимптотически устойчиво при
начальных условиях из области
.
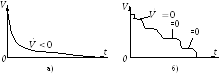
Рисунок 3.5.2.1 – Характеры изменения функции Ляпунова
Пример. Пусть дано уравнение маятника (1), изображенного на рисунке 2.
Рисунок 3.5.2.2 – Математический маятник
, (3.5.2.1)
. (3.5.2.2)
Умножим уравнение
(1) на
.
Получим
.
Это уравнение преобразуется к виду
, (3.5.2.3)
где
. (3.5.2.4)
Т.к. функция
обращается в 0 только при
,
а во всех остальных случаях является
положительной, то функция
является определённо положительной.
Как видно из (4),
– полная энергия системы. В данном
случае
является кинетической энергией, а
второе слагаемое является потенциальной
энергией. В правой части (3) стоит функция
рассеяния
.
Если
,
то рассеяние энергии колебаний
отсутствует. Покажем, что такая ситуация
может быть только в начале координат,
где
.
Для этого предположим, что
. (3.5.2.5)
Т.к. функция
не зависит от
,
то она являетсязнакоотрицательной.
Из условия
следует
. (3.5.2.6)
Подставим (5), (6) в (1). Получим
,
т.е. условие
может выполняться только в начале
координат. Таким образом, выполняются
все условия теоремы Барбашина-Красовского.
Теорема Барбашина-Красовского так же, как и теорема Ляпунова об асимптотической устойчивости, даёт достаточные условия устойчивости. Невозможность найти функцию Ляпунова ещё не говорит о том, что система не является асимптотически устойчивой.
Рассмотренный пример иллюстрирует один из методов построения функций Ляпунова. Функция Ляпунова (4) пропорциональна полной энергии системы: сумме кинетической (первое слагаемое) и потенциальной (второе слагаемое) энергий. Таким образом, полная энергия системы может выступать в роли функции Ляпунова.
3.6 Исследование устойчивости методом фазовой плоскости
Этот метод
применяется к системам первого и второго
порядков. Рассмотрим методику построения
фазовой плоскости нелинейной системы
второго порядка. В качестве координат
примем отклонение
выходной переменной от её установившегося
значения и
.
, (3.6.1)
, (3.6.2)
где
– известные нелинейные функции. Это
система второго порядка. Разделим
уравнение (1) на уравнение (2). В результате
этого исключится время.
. (3.6.3)
Уравнение (3)
является уравнением фазовой траектории
в координатах
первого
порядка. По её поведению можно судить
об устойчивости или неустойчивости
системы.
Метод фазовой плоскости подразделяется на ряд методов. Рассмотрим один из них.
Метод припасовывания (метод сшивания решений).
Рассмотрим нелинейную систему стабилизации
Рисунок 3.6.1 – Структурная схема нелинейной САУ
На рисунке 1
–нелинейная
часть системы,
–передаточная
функция линейной части системы.
Для конкретности будем полагать
–нелинейный
(релейный) регулятор,
–угол поворота
ротора двигателя,
–задающее
воздействие,
–ошибка системы,
–управляющее
воздействие на электродвигатель системы
(управляющее напряжение),
–передаточная
функция электродвигателя.
Эту систему опишем дифференциальными уравнениями
, (3.6.4)
, (3.6.5)
. (3.6.6)
Из (4) и (6) при
следует
. (3.6.7)
Введём новую
переменную
.
Тогда уравнение (7) можно представить
в виде системы
, (3.6.8)
. (3.6.9)
Для получения уравнений фазовых траекторий разделим уравнение (9) на уравнение (8), получим
. (3.6.10)
В уравнении (10)
разделим переменные с учётом того, что
кусочно-постоянная функция (релейное
управление).
. (3.6.11)
Для интегрирования уравнения (11) в левой и правой частях можно применить табличные интегралы.
Рассмотрим
различные релейные элементы
и соответствующие им фазовые траектории,
изображенные на рис. 2-5.
Геометрическое место точек на фазовой плоскости, в которых происходит переключение реле, называется линией переключения (штриховые линии на рис. 2-5).
В случае рис. 2 фазовая траектория стремится к началу координат, где, вследствие отсутствия зоны нечувствительности в регуляторе, установится режим с высокочастотными противовключениями электродвигателя, что нежелательно.
Рисунок 3.6.2 – а) статическая характеристика регулятора (двухпозиционное реле), б) фазовая траектория
Рисунок 3.6.3 – а) статическая характеристика регулятора (трехпозиционное реле), б) фазовая траектория
Рисунок 3.6.4 – а) статическая характеристика регулятора (двухпозиционное реле с гистерезисом), б) фазовая траектория, в) переходный процесс
В случае рис. 3 в
установившемся режиме угол поворота
двигателя будет лежать в зоне
нечувствительности реле, скорость
будет равна нулю, электродвигатель
включаться не будет.
В случае рис. 4, 5 фазовые траектории стремятся к предельному циклу как снаружи его, так и внутри (устойчивый предельный цикл – автоколебания).
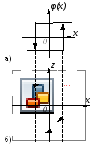
Рисунок 3.6.5 – а) статическая характеристика регулятора (двухпозиционное реле с гистерезисом), б) фазовая траектория, в) переходный процесс