2.14 Порядок синтеза цифровых систем управления

Первый способ. (Иващенко Н.Н. Автоматическое регулирование, 1978, с. 669-670). Рассматривается система с неизвестной передаточной функцией , представленная на рис. 1, с обозначениями, совпадающими с обозначениями рис. 2.8.2 и 2.8.6.

Рисунок 2.14.1 – Структурная схема САУ с ЦВМ

Задача: найти закон управления в зависимости от.

Порядок синтеза.

1. Дискретная передаточная функция непрерывной части системы определяется по зависимости

.

2. Находится дискретная передаточная функция разомкнутой системы

.

3. С помощью -преобразования (2.13.4) находим

,

где – неизвестная передаточная функция.

4. С помощью методов, разработанных для непрерывных систем, синтезируется .

5. С помощью обратного -преобразования (2.13.4) находится дискретная передаточная функция

,,.

6. По функции находится закон управления

.

В результате найден дискретный закон управления.

Второй способ (см. курсовую работу).

Сначала рассматривается непрерывная система управления с неизвестной передаточной функцией .

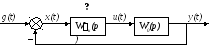
Рисунок 2.14.2 – Структурная схема эквивалентной непрерывной САУ с ЦВМ

С помощью известных методов, разработанных для непрерывных систем, синтезируется передаточная функция , затем кприменяется формула Тастина (2.10.9)

,

откуда аналогично (2.10.11) получаем

. (2.14.1)

В найденную передаточную функцию делаем подстановку (1). Получаем дискретную передаточную функцию корректирующего звена, а по этой передаточной функции находится дискретный закон управления.

3 Нелинейные системы автоматического управления

По математическому описанию САУ делятся на линейные и нелинейные. Нелинейной САУ называется САУ, содержащая хотя бы одно нелинейное звено, т.е. звено, описываемое нелинейными уравнениями. Математический аппарат исследования нелинейных САУ более сложен и менее универсален по сравнению с математическим аппаратом линейных САУ. Поэтому естественно желание разработчиков САУ заменить исследование нелинейных САУ исследованием близких им по динамике линейных САУ. В подразделе 1.1 был рассмотрен приём линеаризации гладких нелинейностей, основанный на разложении в ряд Тейлора.

В этом разделе будут рассматриваться нелинейные САУ, которые не могут быть линеаризованы с помощью разложения нелинейности в ряды Тейлора.

3.1 Основные нелинейные звенья

Наиболее часто встречаются следующие нелинейные звенья (правее статических характеристик даны синусоидальный входной сигнал и выходной сигнал):

Рисунок 3.1.1 – Звено с насыщением

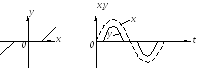
Рисунок 3.1.2 – Звено с зоной нечувствительности

Рисунок 3.1.3 – Идеальное двухпозиционное реле (кулоново трение)

Рисунок 3.1.4 – Идеальное трёхпозиционное реле

Рисунок 3.1.5 – Двухпозиционное реле с гистерезисом

Рисунок 3.1.6 – Трехпозиционное реле с гистерезисом

Рисунок 3.1.7 – Петля гистерезиса (звено с мёртвым ходом)

Рисунок 3.1.8 – Звено выделения модуля

Хотя нелинейности и затрудняют исследование САУ, они часто специально вводятся в систему управления, например, для компенсации уже существующих в системе управления нежелательных нелинейностей. Кроме того, оптимальные по быстродействию САУ всегда являются нелинейными.