
- •Алгебра та геометрія: основи лінійної алгебри
- •Практичне заняття № 1 Тема: Матриці. Дії з матрицями
- •Транспонування матриць
- •Додавання матриць
- •Множення матриці на число
- •Добуток матриць
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 2 Тема: Перестановки. Підстановки. Визначник та його властивості
- •Властивості визначників
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 3 Тема: Методи знаходження оберненої матриці
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 4 Тема: Системи лінійних алгебраїчних рівнянь (слар). Теорема Крамера. Матричний метод розв’язання слар
- •Методи розв’язання слар. Метод Крамера
- •Матричний спосіб розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 5 Тема: Ранг матриці. Теорема Кронекера-Капеллі. Метод Гауса розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Завдання для самостійного розв’язування
- •Практичне заняття № 7 Тема: Систематизація та узагальнення знань з розділів лінійної алгебри: «Матриці», «Визначники», «Системи лінійних алгебраїчних рівнянь»
- •Тест для самоперевірки
- •Практичне заняття № 8 Тема: Модульна контрольна робота № 1 (приклад)
- •Завдання для самостійного опрацювання
- •Додаткові завдання для самостійного розв’язування
- •Питання для самоконтролю
- •Індивідуальне завдання
- •Завдання для підвищення рейтингу студента
- •Відповіді
- •Література
- •Додаток а
- •Індивідуальне завдання з курсу «Алгебра та геометрія» за розділом: Основи лінійної алгебри
Матричний спосіб розв’язання слар
Систему
![]() лінійних алгебраїчних рівнянь ізn
невідомими (*) можна записати в матричному
виді:
лінійних алгебраїчних рівнянь ізn
невідомими (*) можна записати в матричному
виді:
![]() ,
деA
– матриця системи, X
– матриця-стовпець невідомих
,
деA
– матриця системи, X
– матриця-стовпець невідомих
![]() ,
аB
– матриця-стовпець вільних членів. Якщо
A
– невироджена матриця, то після множення
ліворуч на
,
аB
– матриця-стовпець вільних членів. Якщо
A
– невироджена матриця, то після множення
ліворуч на
![]() обидві частини матричного рівняння
обидві частини матричного рівняння![]() ,
одержимо
,
одержимо![]() .
Taк як
.
Taк як![]() ,
то очевидно
,
то очевидно
![]() .
.
Приклади розв’язування задач
Розв’яжіть систему лінійних алгебраїчних рівнянь: а) за теоремою Крамера; б) матричним способом:
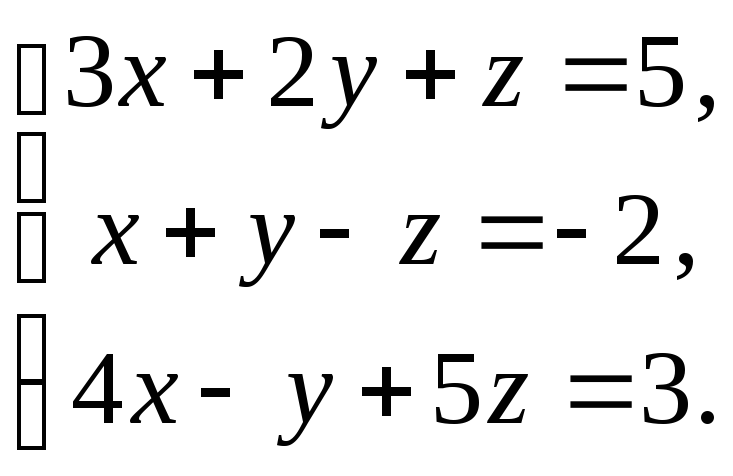
Розв’язання:
а)
Обчислимо визначник системи
![]() й визначники
й визначники![]() ,
,![]() ,
,![]() ,
що отримані з визначника
,
що отримані з визначника![]() заміною першого, другого, третього
стовпців стовпцем вільних членів:
заміною першого, другого, третього
стовпців стовпцем вільних членів:
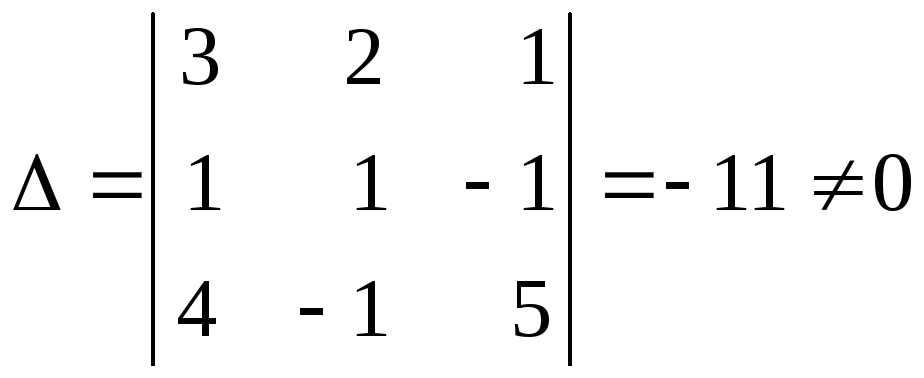 ,
,
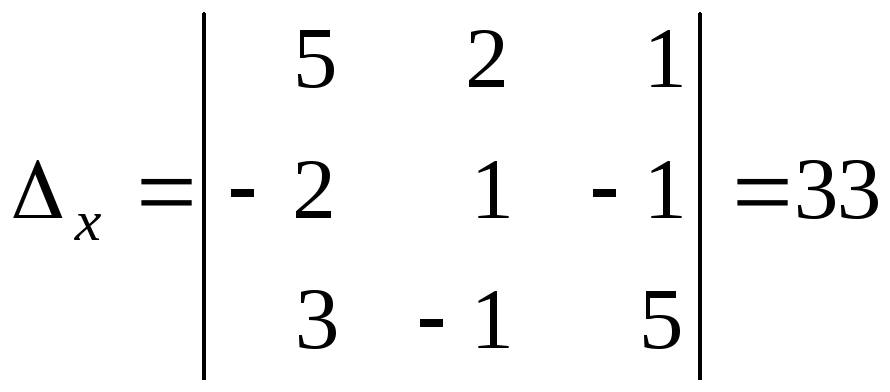 ,
,
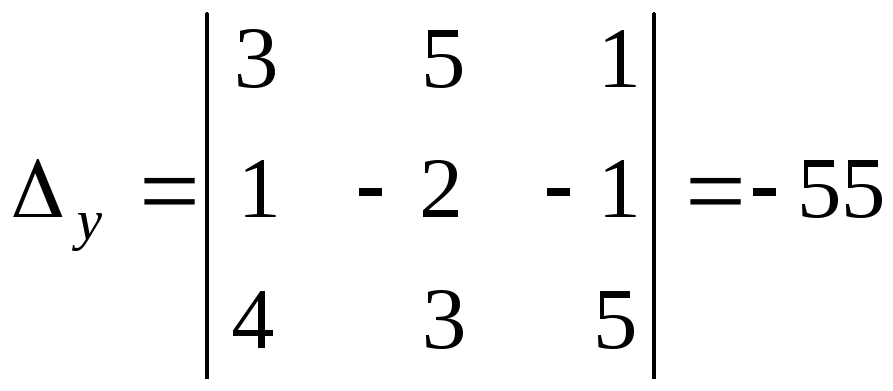 ,
,
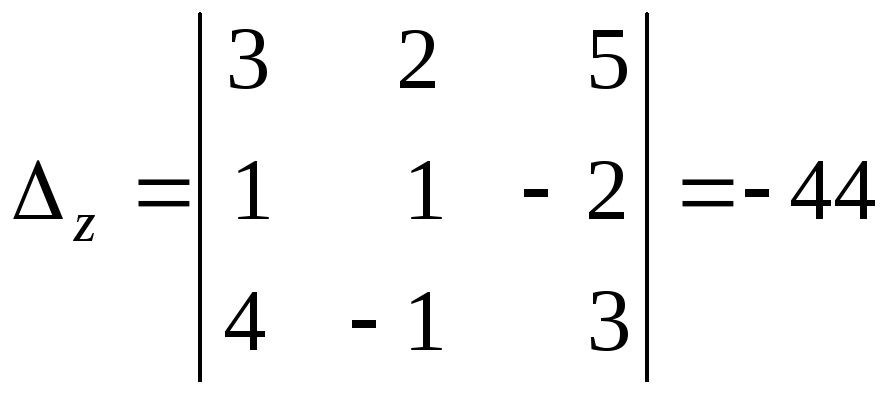 .
.
За формулами Крамера одержуємо єдиний розв’язок системи:
![]() ,
,
![]() ,
,![]() .
.
Відповідь:
![]() .
.
б) Перепишемо вихідну систему у вигляді
![]() ,
,
де
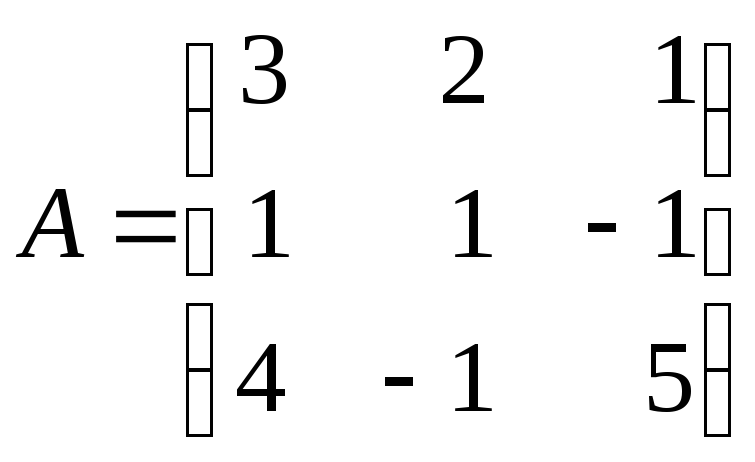 ,
,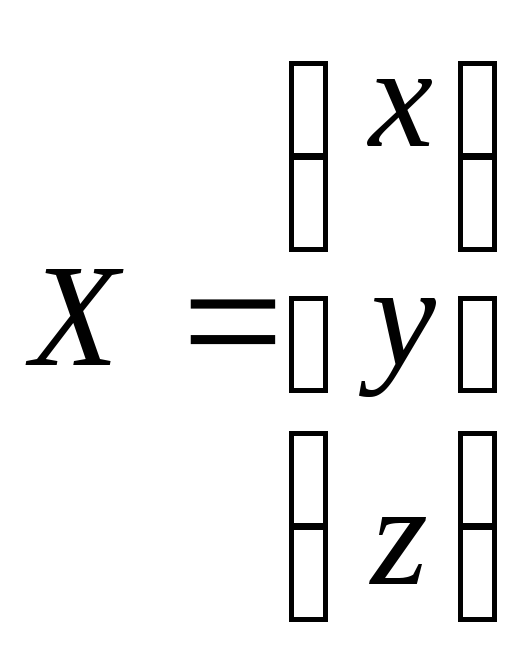 ,
,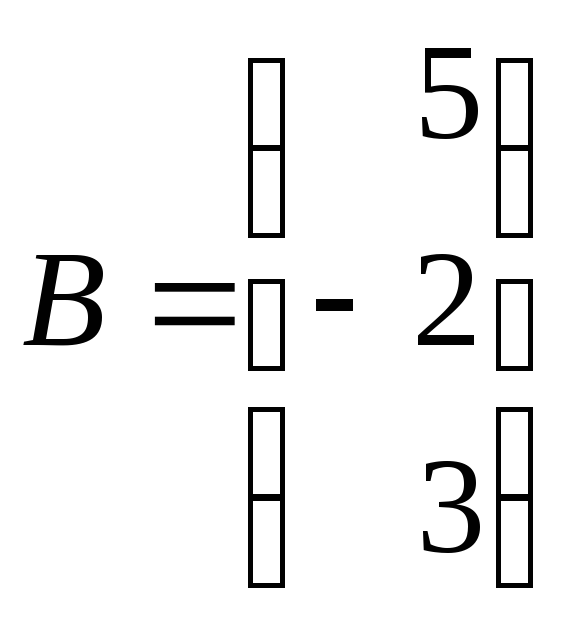 .
.
Оскільки
![]() ,
то матриця
,
то матриця![]() має обернену. Знайдемо її методом
алгебраїчних доповнень:
має обернену. Знайдемо її методом
алгебраїчних доповнень:
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
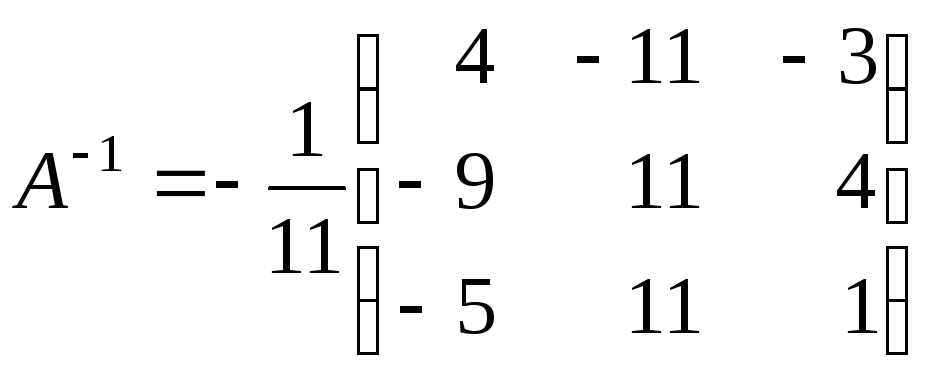 .
.
Знайдемо розв’язок:
 .
.
Відповідь:
![]() .
.
Розв’яжіть СЛАР: а) за правилом Крамера; б) шляхом зведення її до матричного рівняння. Порівняйте отримані результати.
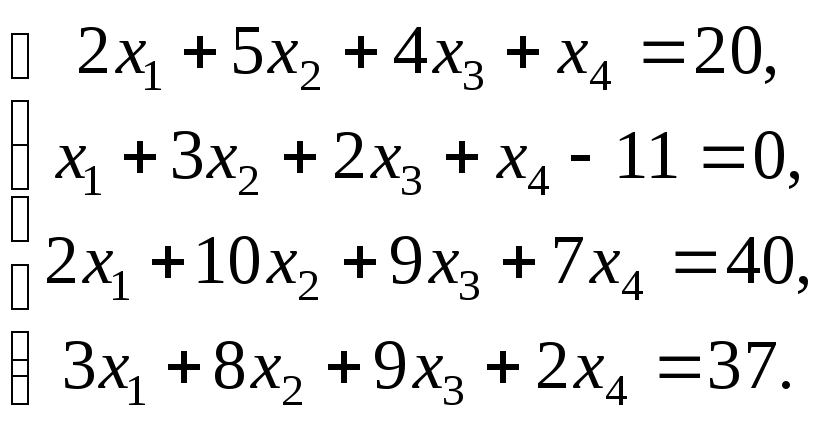
Розв’язання:
а) Знайдемо визначник матриці системи:
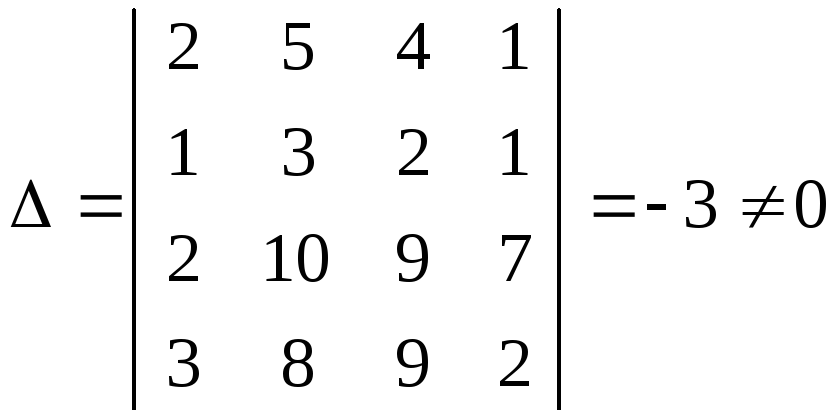 .
.
За
теоремою Крамера дана СЛАР має єдиний
розв’язок. Знайдемо значення визначників
![]() матриць, отриманих з вихідної заміною
матриць, отриманих з вихідної заміною![]() -ого
стовпця стовпцем вільних членів.
Отримаємо:
-ого
стовпця стовпцем вільних членів.
Отримаємо:
 ,
,
 ,
,
 ,
,
 .
.
Значення змінних знайдемо зі співвідношень:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
б) Запишемо вихідну систему у матричному вигляді:
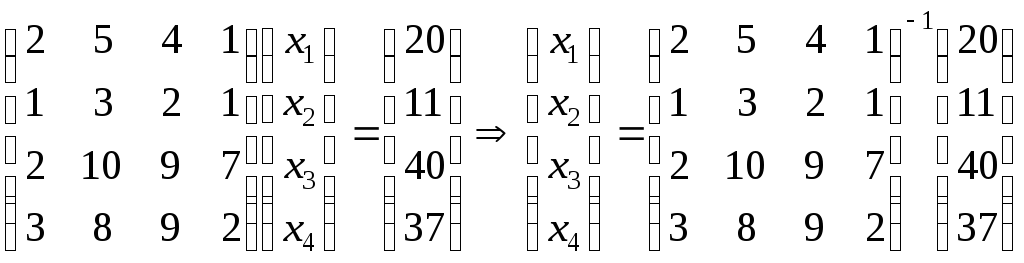 .
.
На стор. 26-28 знайдено обернену матрицю:
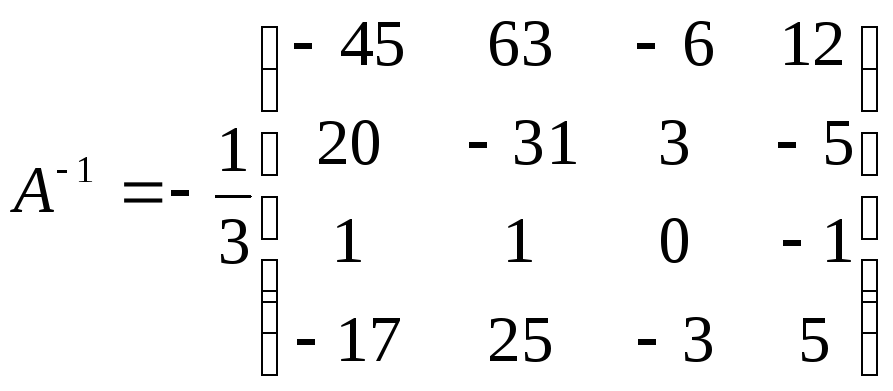 .
.
Тоді:
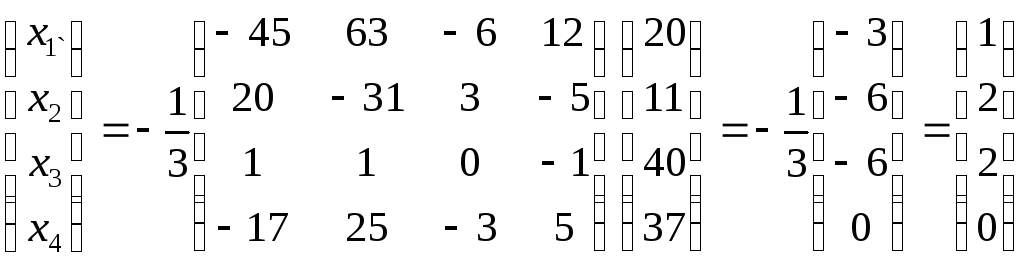 .
.
Отже,
![]() .
Як бачимо, розв’язки СЛАР, що знайдені
різними методами, співпадають між собою.
.
Як бачимо, розв’язки СЛАР, що знайдені
різними методами, співпадають між собою.
Підстановкою
отриманих значень у вихідну систему
легко переконатись, що набір
![]() дійсно є її розв’язком.
дійсно є її розв’язком.
Задачі для самостійного розв’язування
Розв’яжіть наступні СЛАР за теоремою Крамера:
а)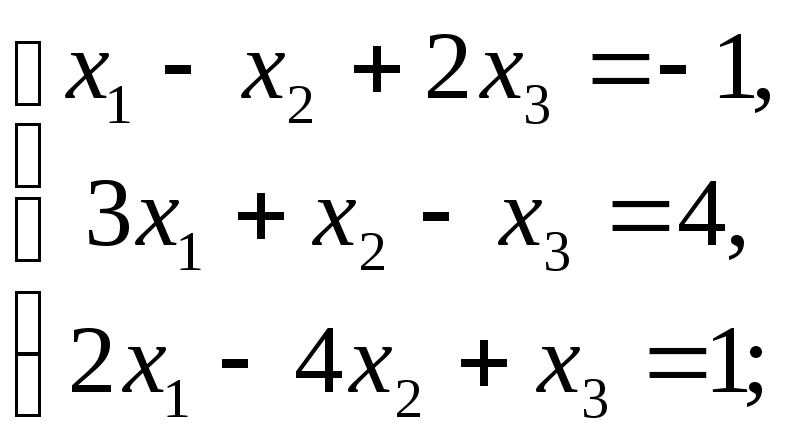 б)
б)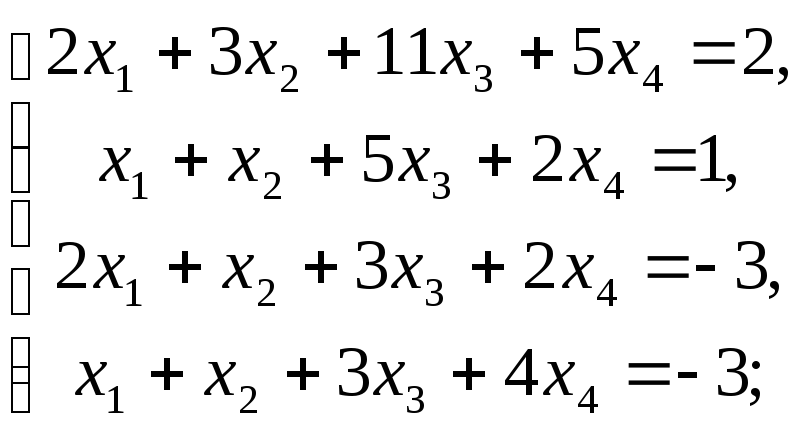 в)
в)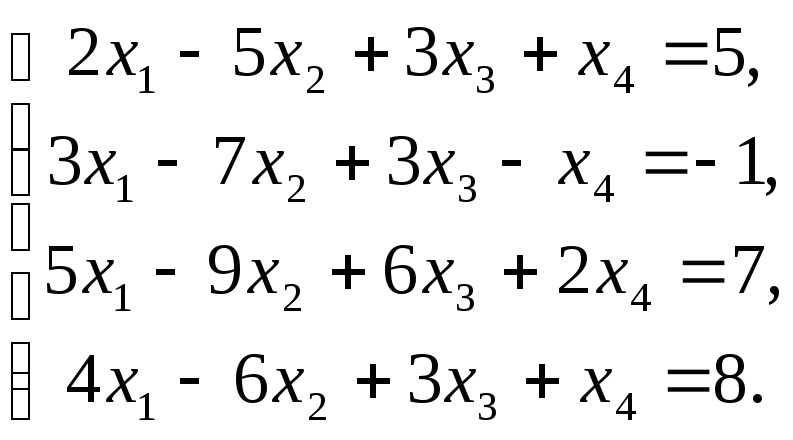
Якщо система визначена, то знайдіть її розв’язок: а) за теоремою Крамера; б) матричним методом:
1)
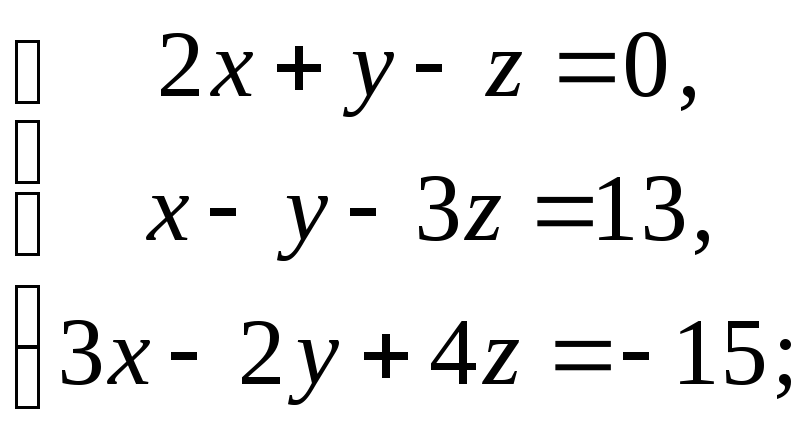 2)
2)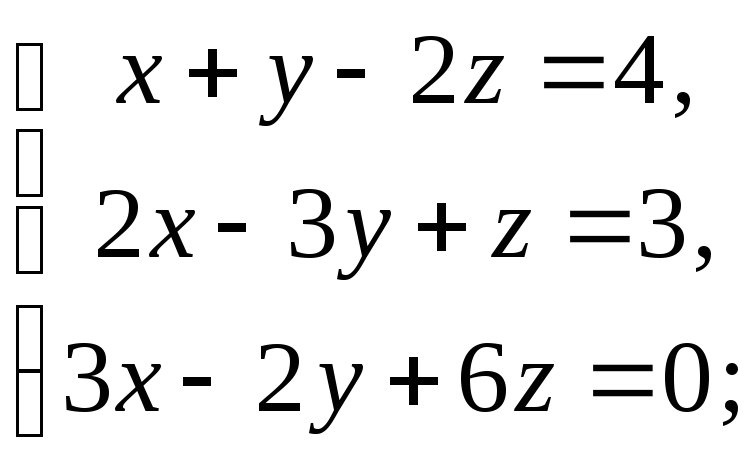 3)
3)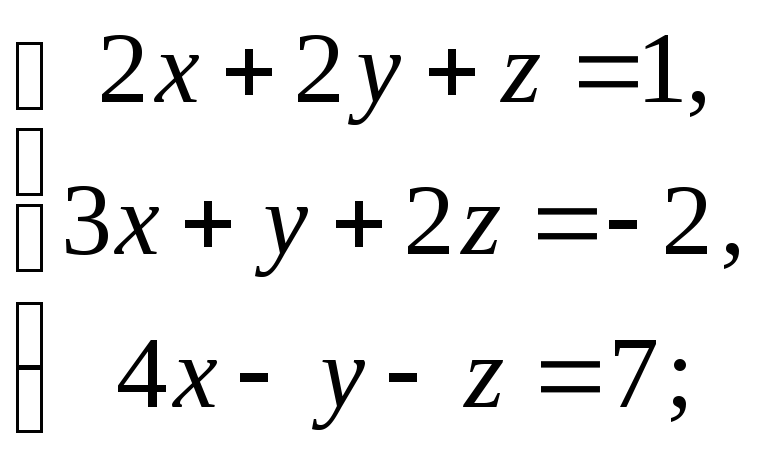
4)
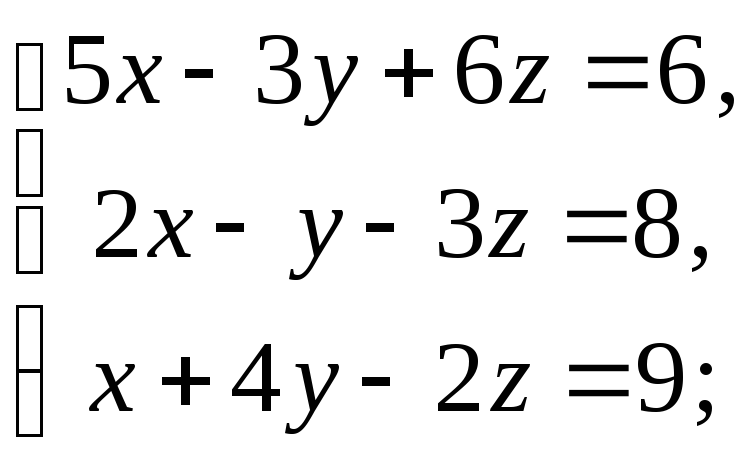 5)
5)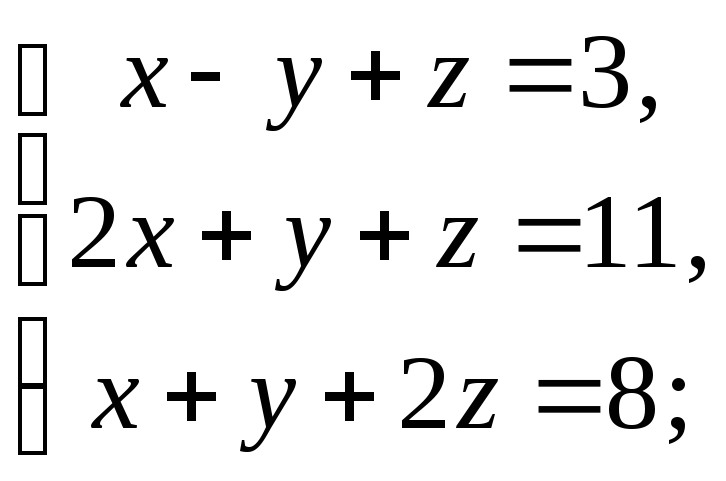 6)
6)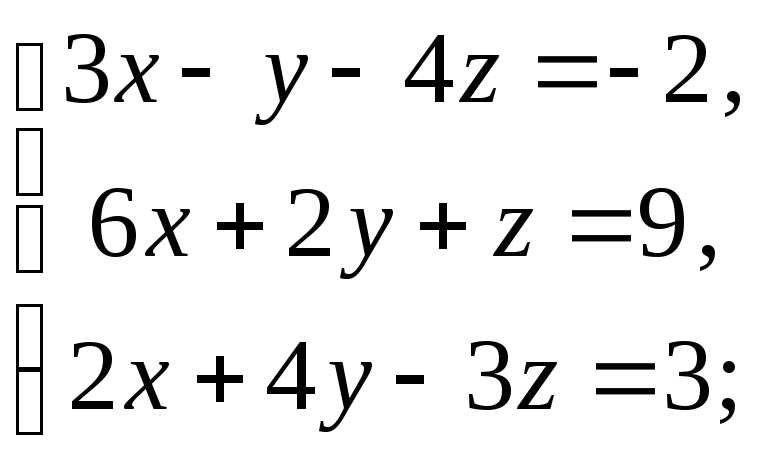
7)
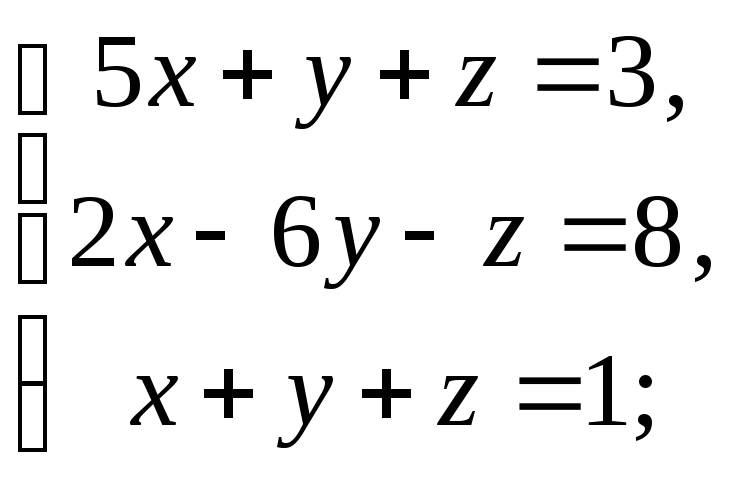 8)
8)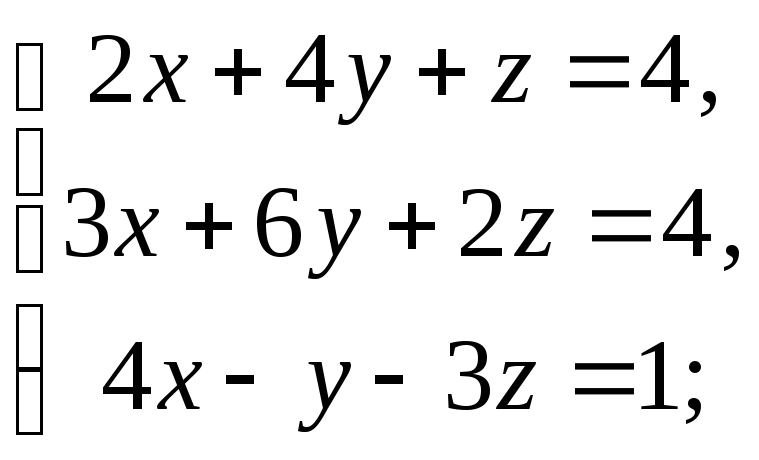 9)
9)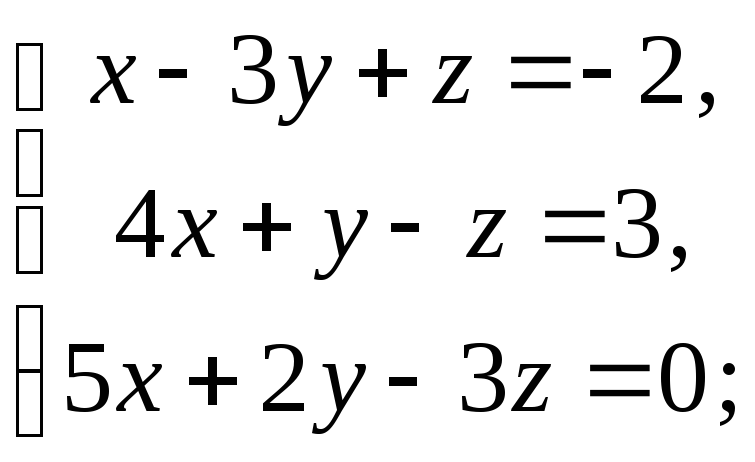
10)
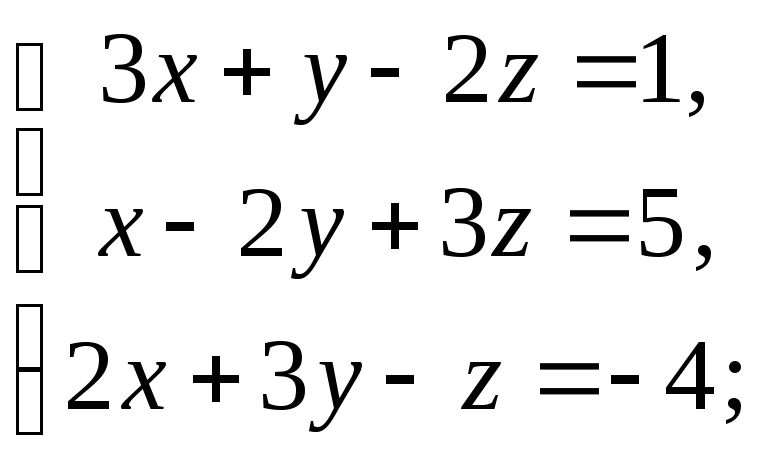 11)
11)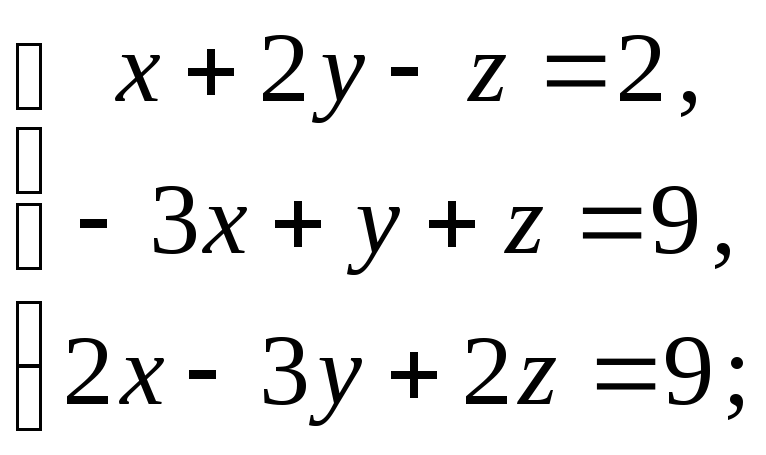 12)
12)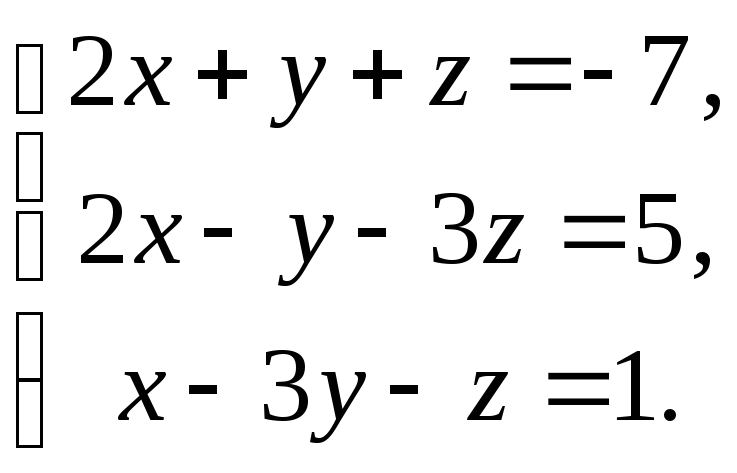
Практичне заняття № 5 Тема: Ранг матриці. Теорема Кронекера-Капеллі. Метод Гауса розв’язання слар
Елементарними перетвореннями рядів матриці називають: 1) переміна місцями двох рядків матриці; 2) додавання до елементів одного рядка відповідних їм елементів іншого, помножених на ненульове число.
Теорема.
Якщо від матриці
![]() до матриці
до матриці![]() можна перейти скінченим числом
елементарних перетворень рядків, то
всякий розв’язок системи лінійних
алгебраїчних рівнянь, що відповідає
матриці
можна перейти скінченим числом
елементарних перетворень рядків, то
всякий розв’язок системи лінійних
алгебраїчних рівнянь, що відповідає
матриці![]() ,
служить розв’язком системи з матрицею
,
служить розв’язком системи з матрицею![]() і навпаки, тобто розглянуті системи
рівнянь еквівалентні.
і навпаки, тобто розглянуті системи
рівнянь еквівалентні.
Матриця називається ступінчастою, якщо в ній під кожним першим ненульовим елементом рядка стоять тільки нулі.
Рангом
матриці
![]() називається число
називається число![]() ненульових рядків в матриці ступінчастого
виду.
ненульових рядків в матриці ступінчастого
виду.
Теорема
(теорема Кронекера-Капеллі)
Система лінійних алгебраїчних рівнянь
сумісна тоді й тільки тоді, коли ранг
матриці системи дорівнює рангу розширеної
матриці цієї системи, тобто
![]() .
.
Зауваження. 1) Якщо ранг матриці сумісної СЛАР дорівнює числу невідомих, то система має єдиний розв’язок, тобто є визначеною. 2) Якщо ранг матриці сумісної СЛАР менше числа невідомих, то система має нескінченну множину розв’язків, тобто є невизначеною.
Алгоритм розв’язку системи рівнянь (*) методом Гауса:
Запишемо розширену матрицю
 вихідної системи рівнянь.
вихідної системи рівнянь.Приведемо матрицю
 до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці
до ступінчастого виду за допомогою
елементарних перетворень рядків. Якщо
в отриманій ступінчастій матриці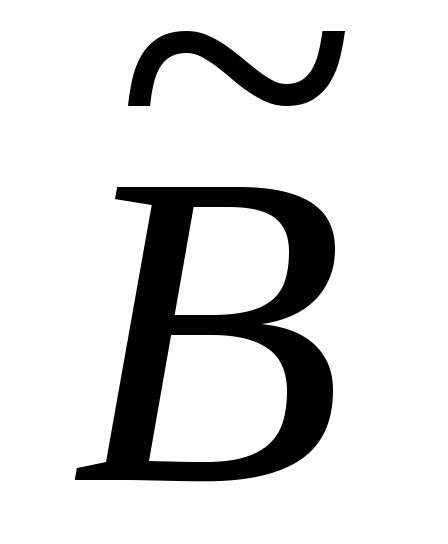 є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).
є рядок, у якому перший ненульовий
елемент перебуває на останньому місці,
то вихідна система розв’язків не має
(несумісна).Якщо система рівнянь сумісна, то в системі рівнянь із матрицею
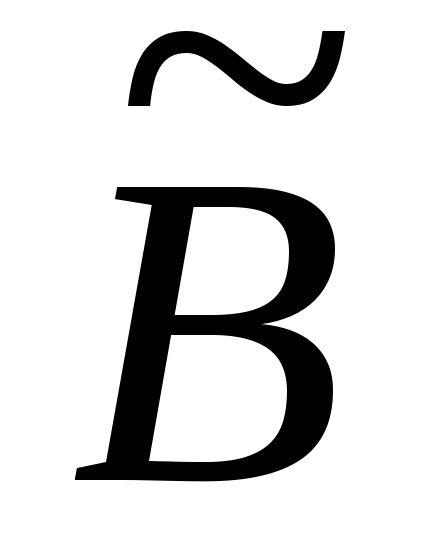 необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці
необхідно відкинути рівняння, які
відповідають нульовим рядкам матриці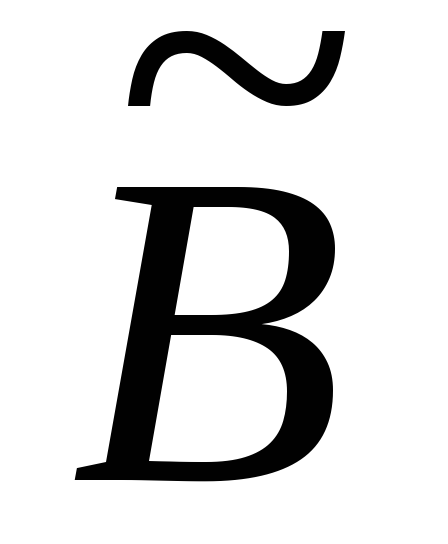 .
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.
.
У рівняннях, що залишилися, виділяємо
головні невідомі (визначник, складений
з коефіцієнтів при них, не дорівнює
нулю), а члени з вільними невідомими
переносимо в праві частини.Послідовно виражаємо головні невідомі через вільні, рухаючись від останнього рівняння до першого, отримаємо загальний розв’язок системи.
Надаючи вільним невідомим різні числові значення й обчислюючи відповідні значення головних невідомих, одержимо різні розв’язки вихідної системи лінійних алгебраїчних рівнянь, тобто отримаємо частинні розв’язки системи.
Приклад. Розв’яжіть системи лінійних алгебраїчних рівнянь:
1)
![]() 2)
2)![]() 3)
3)![]()
Відповідь:
1)
![]() ,
,![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
