
- •Алгебра та геометрія: основи лінійної алгебри
- •Практичне заняття № 1 Тема: Матриці. Дії з матрицями
- •Транспонування матриць
- •Додавання матриць
- •Множення матриці на число
- •Добуток матриць
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 2 Тема: Перестановки. Підстановки. Визначник та його властивості
- •Властивості визначників
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 3 Тема: Методи знаходження оберненої матриці
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 4 Тема: Системи лінійних алгебраїчних рівнянь (слар). Теорема Крамера. Матричний метод розв’язання слар
- •Методи розв’язання слар. Метод Крамера
- •Матричний спосіб розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 5 Тема: Ранг матриці. Теорема Кронекера-Капеллі. Метод Гауса розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Завдання для самостійного розв’язування
- •Практичне заняття № 7 Тема: Систематизація та узагальнення знань з розділів лінійної алгебри: «Матриці», «Визначники», «Системи лінійних алгебраїчних рівнянь»
- •Тест для самоперевірки
- •Практичне заняття № 8 Тема: Модульна контрольна робота № 1 (приклад)
- •Завдання для самостійного опрацювання
- •Додаткові завдання для самостійного розв’язування
- •Питання для самоконтролю
- •Індивідуальне завдання
- •Завдання для підвищення рейтингу студента
- •Відповіді
- •Література
- •Додаток а
- •Індивідуальне завдання з курсу «Алгебра та геометрія» за розділом: Основи лінійної алгебри
Приклади розв’язування задач
Знайдіть можливі добутки матриць
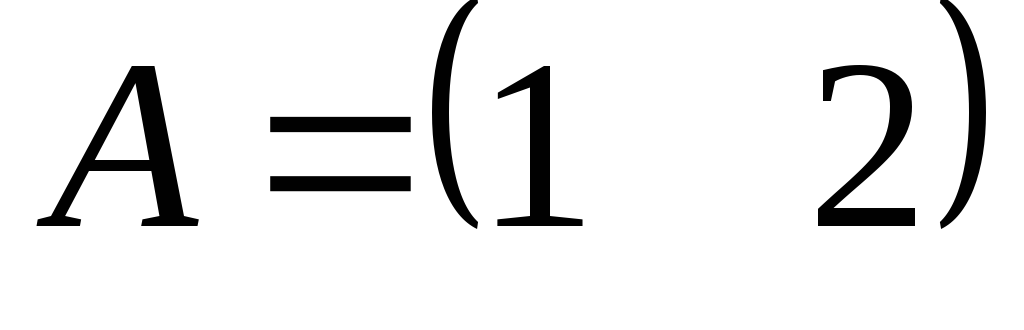 ,
,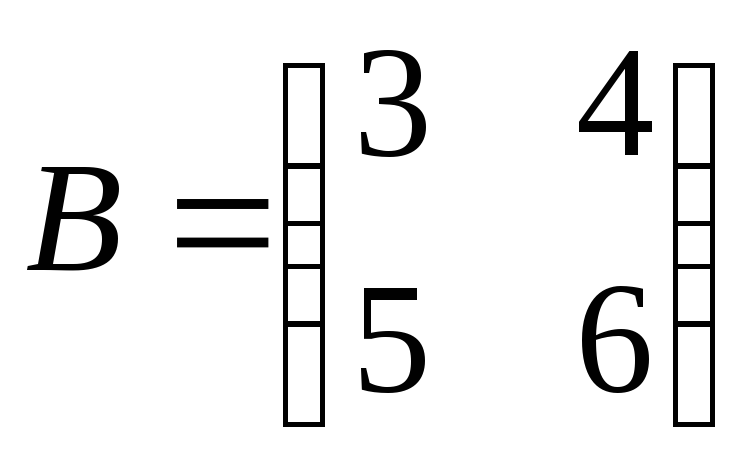 .
.
Розв’язання:
Добуток
![]() існує:
існує:![]() ,
,
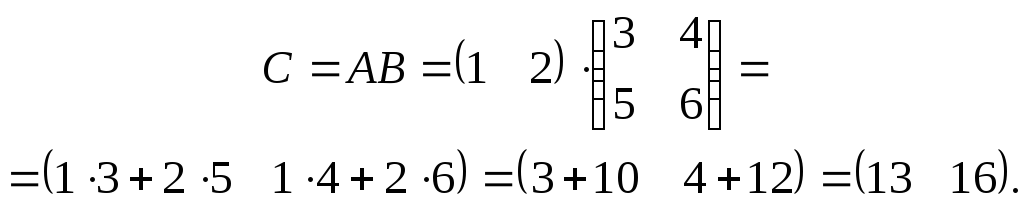
Добуток
![]() – не існує, тому що кількість стовпців
матриці
– не існує, тому що кількість стовпців
матриці![]() (два стовпці) не дорівнює кількості
рядків матриці
(два стовпці) не дорівнює кількості
рядків матриці![]() (один рядок).
(один рядок).
Дано матриці
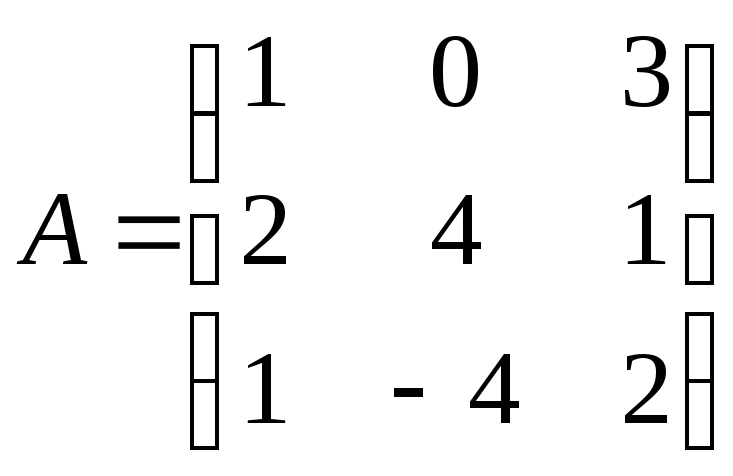 ,
,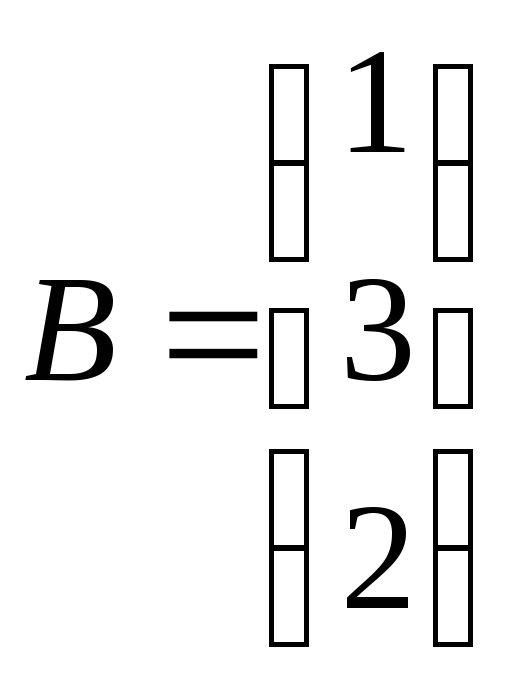 ,
,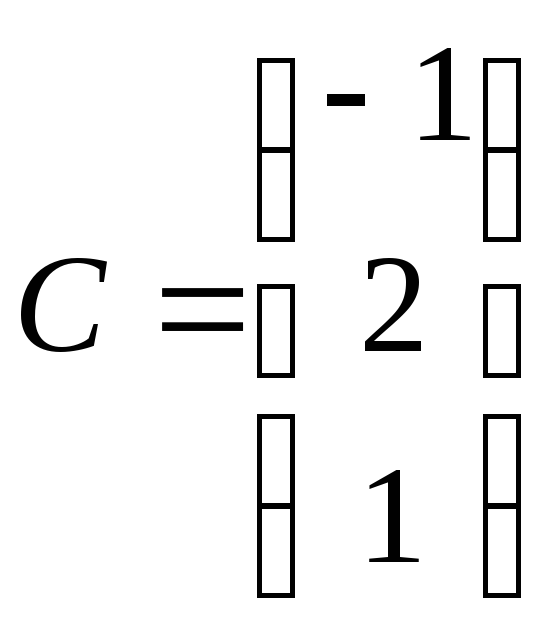 .
Знайдіть
.
Знайдіть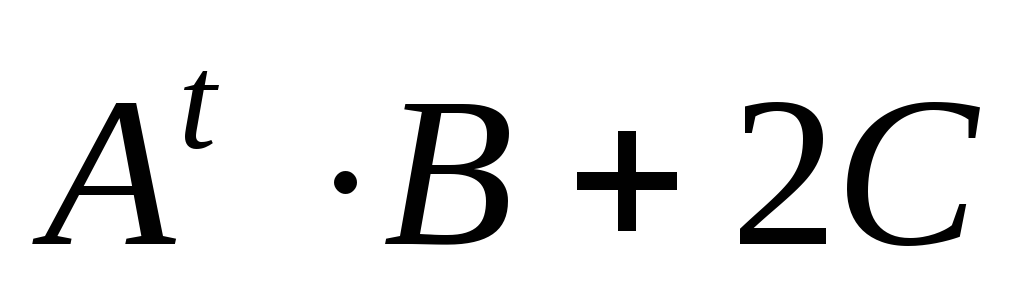 .
.
Розв’язання:
1)
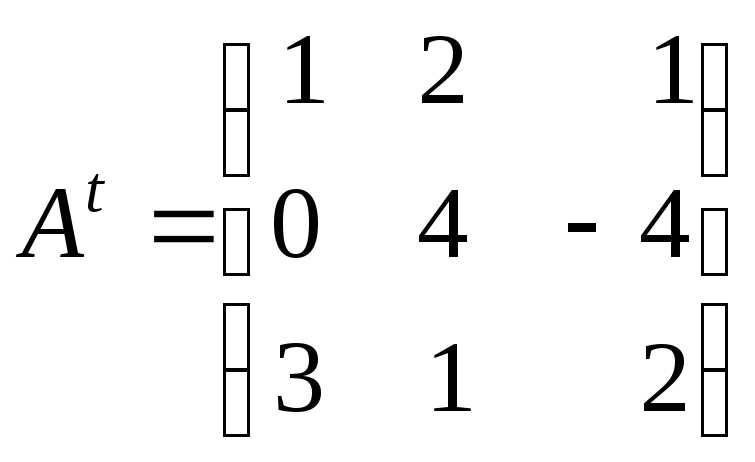 ;
;
2)
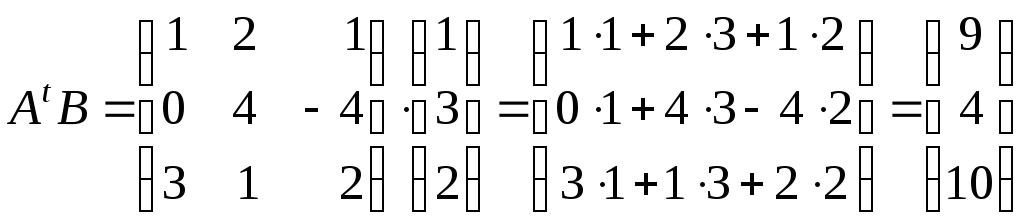 ;
;
3)
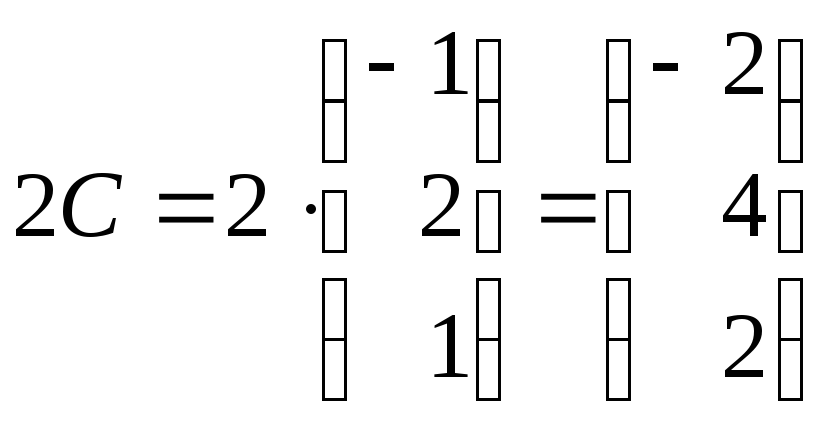 ;
;
4)
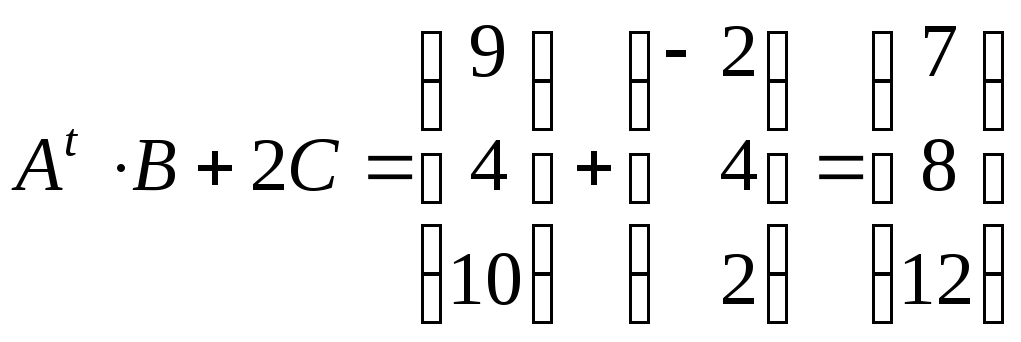 .
.
Дано матрицю
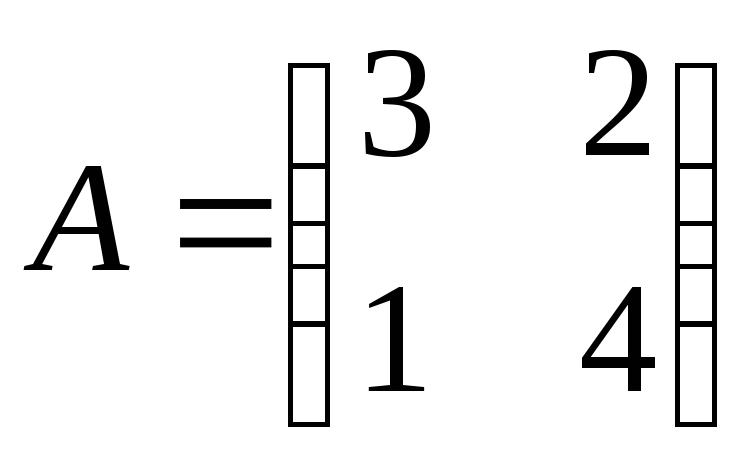 .
Знайдіть
.
Знайдіть .
.
Розв’язання:
![]() ;
;
![]() .
.
За
властивостями добутку матриць:
![]() ,
тому матриці
,
тому матриці![]() та
та![]() є
переставними:
є
переставними:![]() .
.
Дано дві матриці:
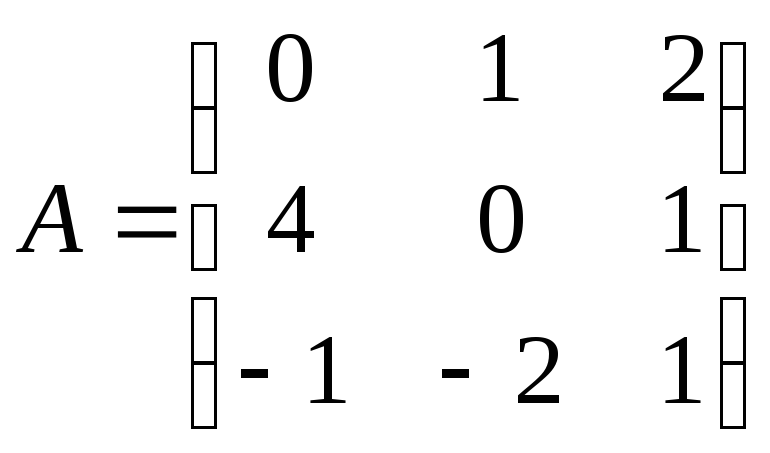 ,
,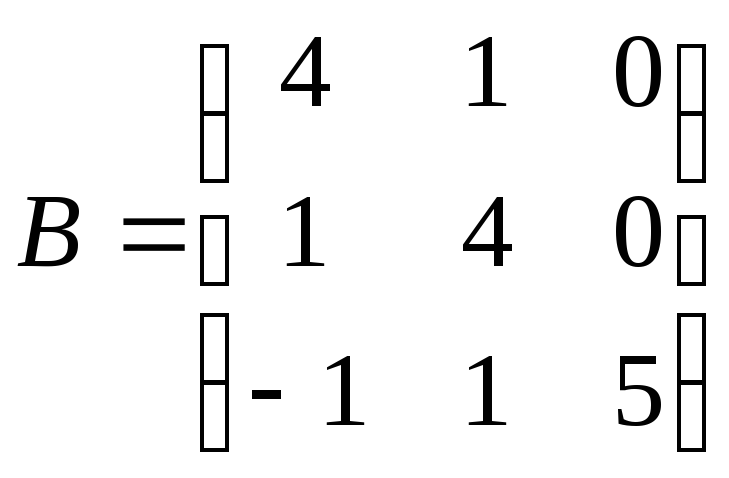 .
Обчисліть:
.
Обчисліть:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Розв’язання:
а)
За означенням добутку матриці на число
обчислимо
![]() та
та![]() :
:
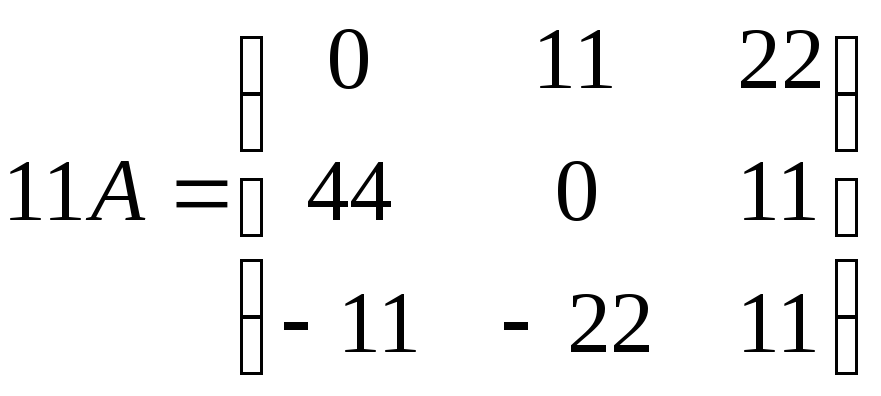 ;
;
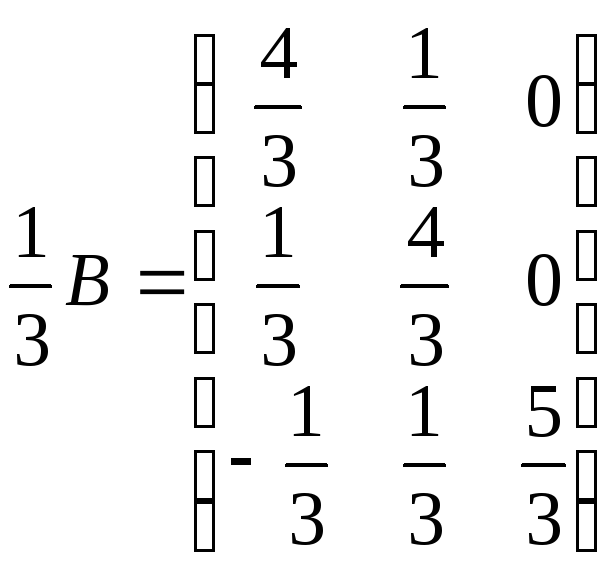 .
.
За правилом додавання матриць отримаємо:
![]()
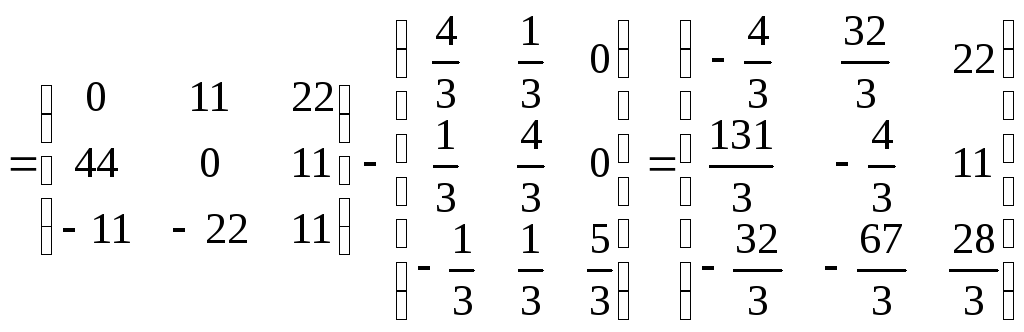 .
.
б)
За означенням транспонованої матриці
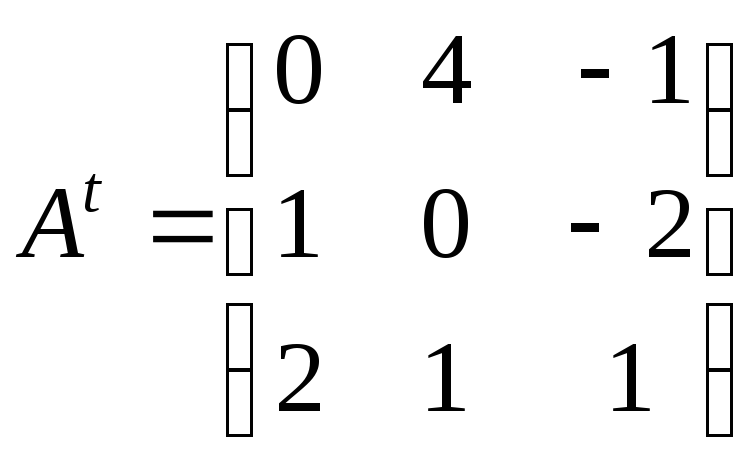 .
Помножимо елементи матриці
.
Помножимо елементи матриці![]() на 3:
на 3:
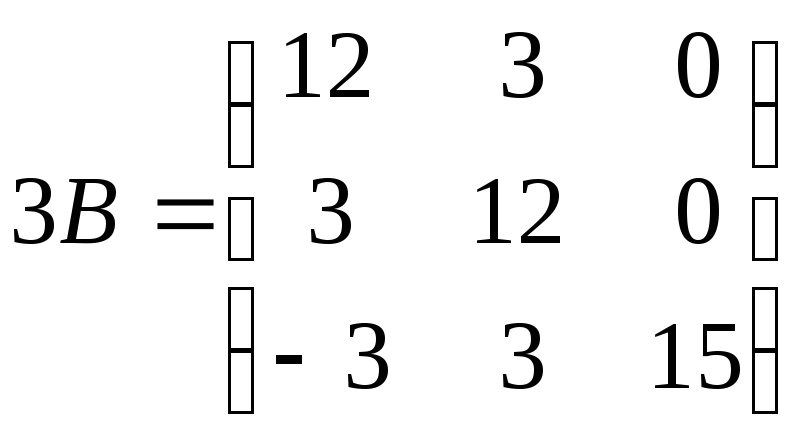 .
.
Тоді
 .
.
в)
Знайдемо матрицю, що дорівнює
![]() .
.
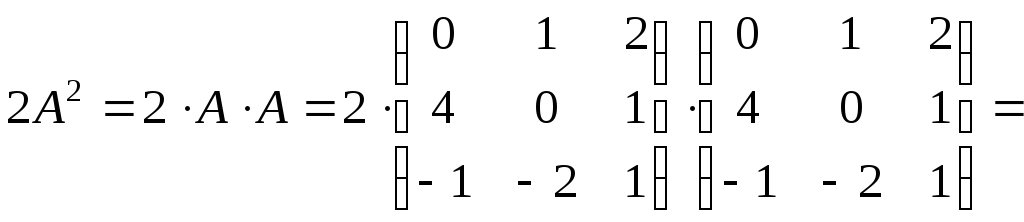
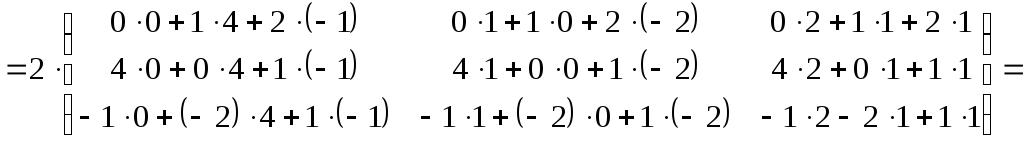
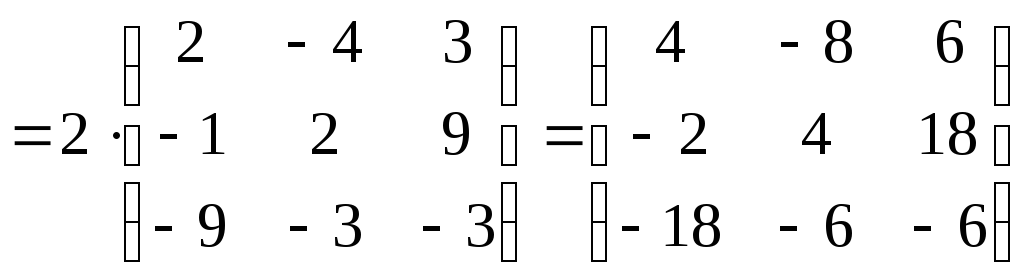 .
.
Зауважимо,
що за властивостями множення
![]() .
.
Тоді
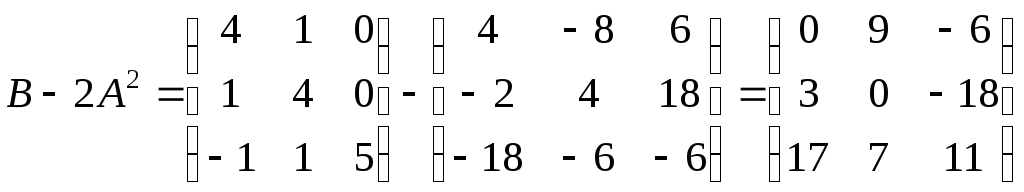 .
.
Матричним рівнянням називають рівняння, невідомим якого є матриця. Коренем матричного рівняння є матриця, яка при підстановці її у рівняння перетворює його на вірну тотожність. Два рівняння називають рівносильними, якщо множини їх розв’язків співпадають. Для розв’язання матричних рівнянь використовують такі перетворення, як додавання до обох частин рівняння однієї і тієї ж матриці (за правилом додавання матриць), множення обох частин рівності на ненульове число, множення обох частин рівності на ненульову матрицю (за правилом множення матриць).
Знайдіть матрицю
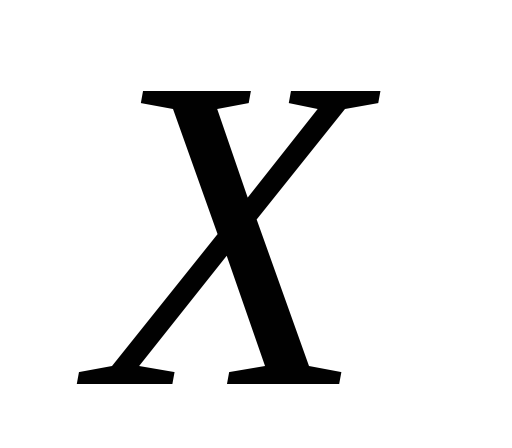 ,
якщо
,
якщо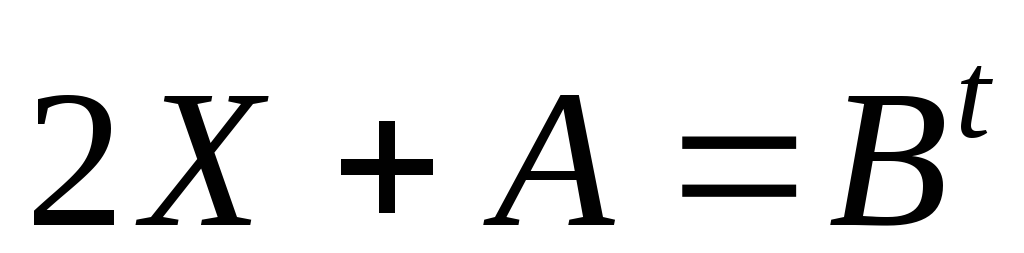 (
( та
та – матриці з прикладу 4).
– матриці з прикладу 4).
Розв’язання:
Додамо
до обох частин даного рівняння матрицю
![]() ,
а потім помножимо обидві частини на
число
,
а потім помножимо обидві частини на
число![]() .
Отримаємо:
.
Отримаємо:
![]() .
.
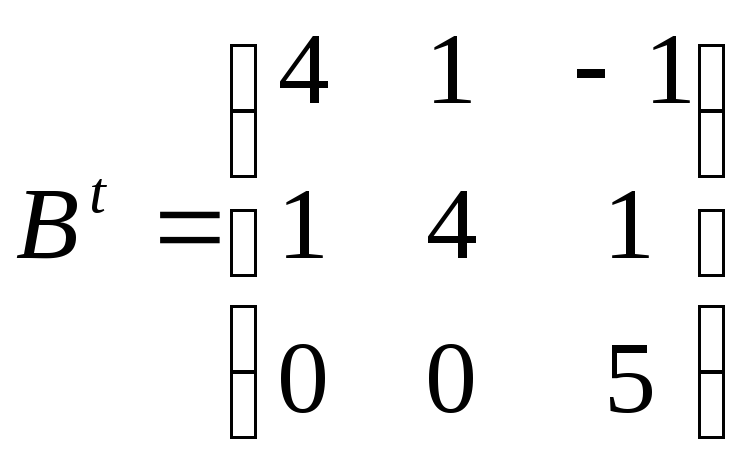 ,
,
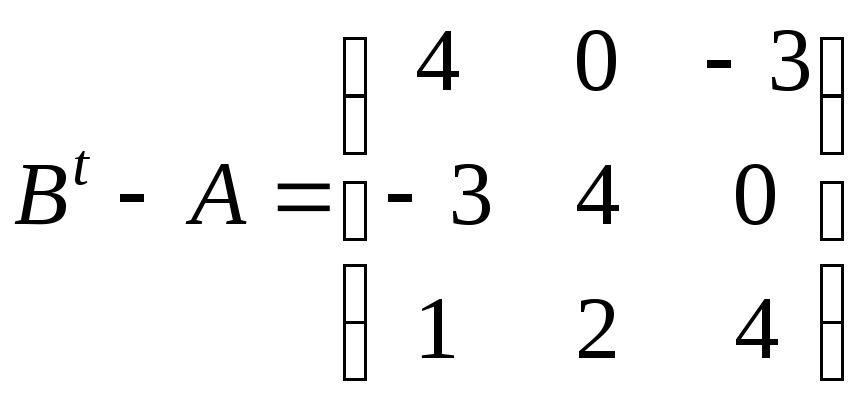
![]()
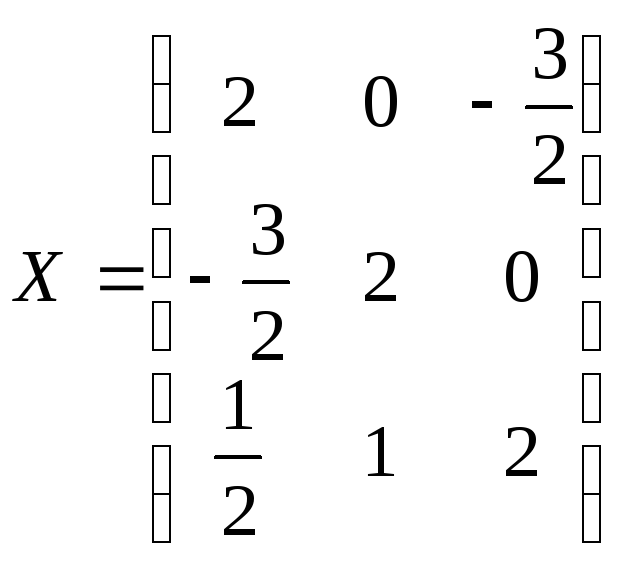 .
.
Перевірте, чи виконуються для матриць
 та
та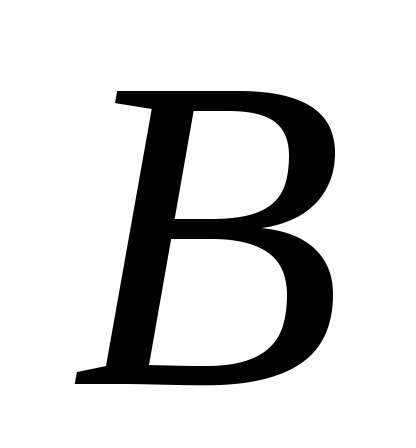 з прикладу 4 рівності:
з прикладу 4 рівності:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Розв’язання:
а) Перевіримо виконання даної рівності. Для цього перетворимо ліву та праву його частини:
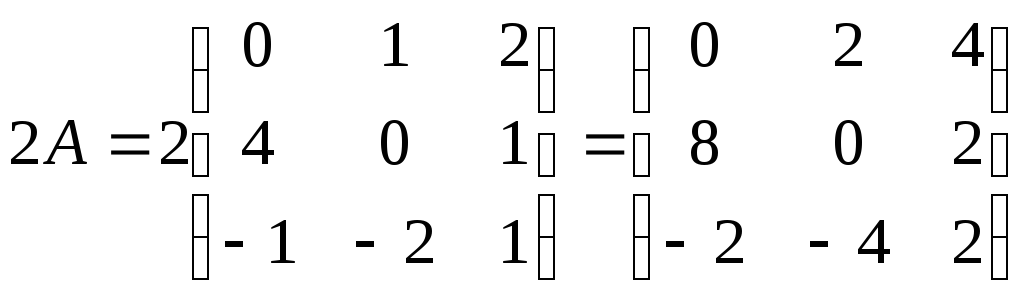 ;
;
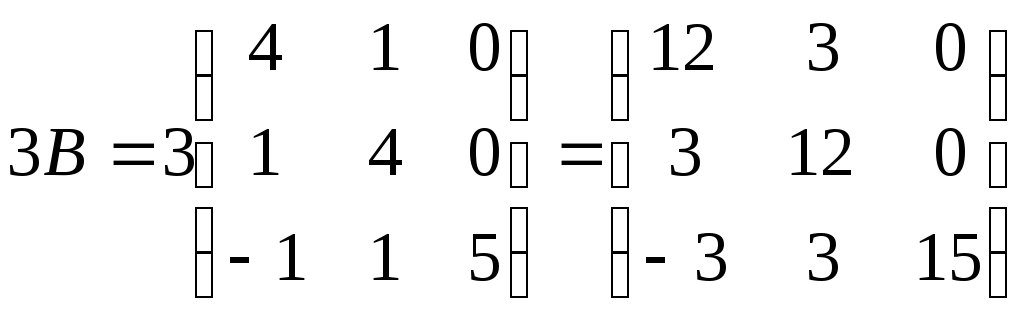 ;
;
 ;
;
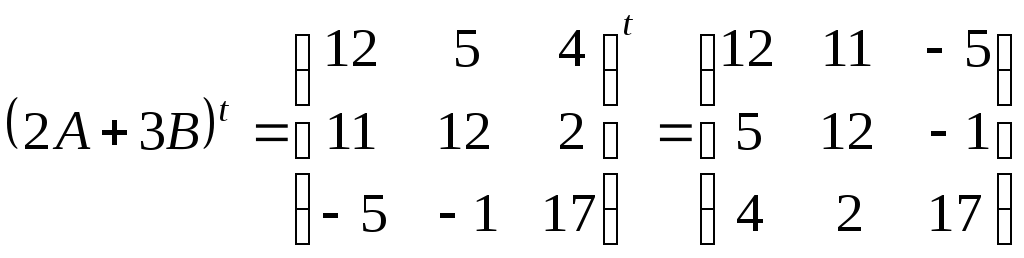 .
.
З іншого боку:
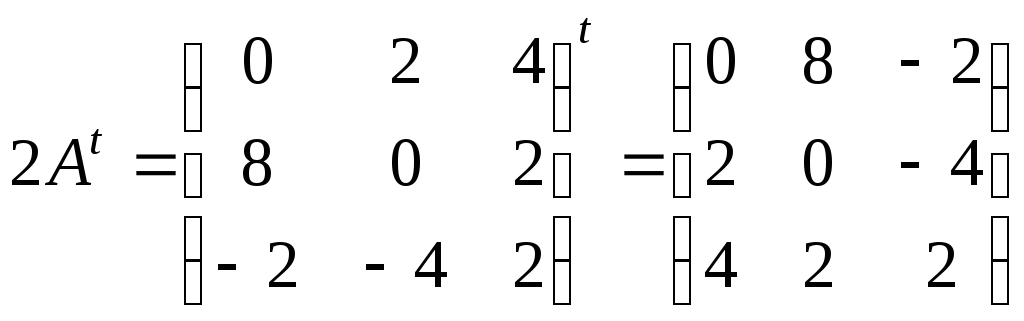 ;
;
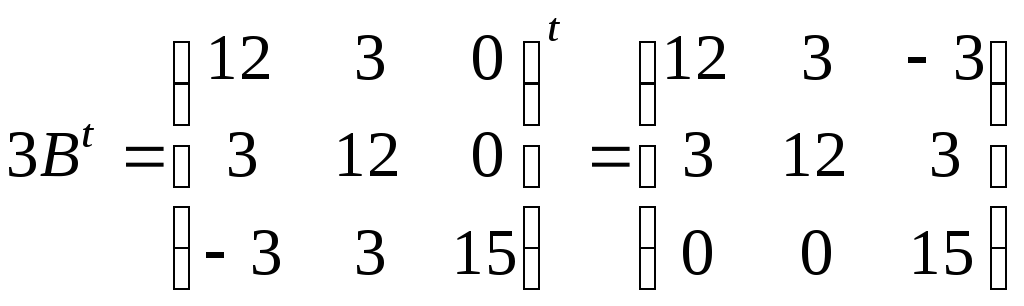 ;
;
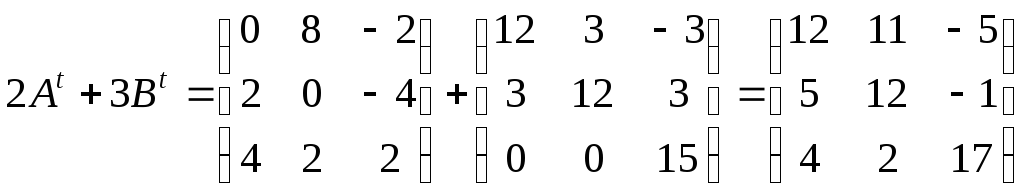 .
.
Отримаємо
вірну рівність:
![]() .
.
б) За означенням добутку матриць:
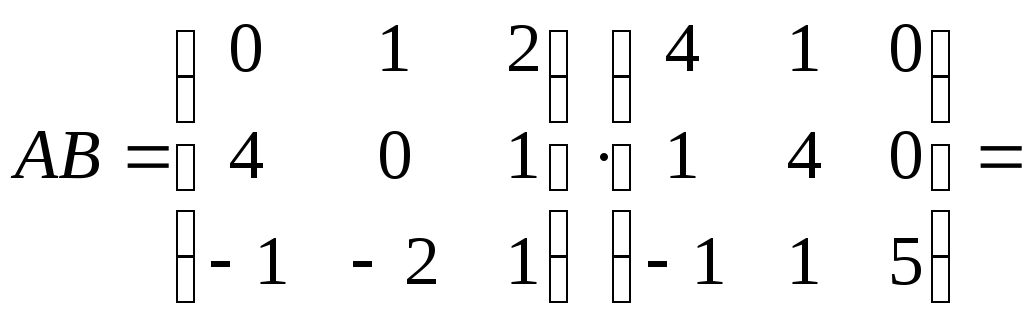
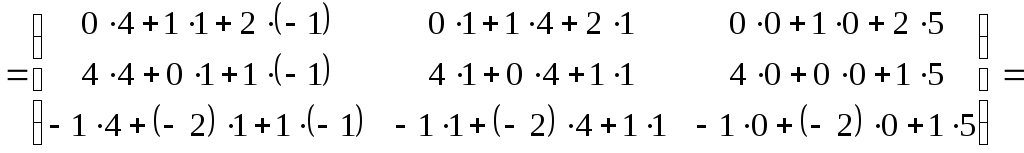
 ;
;
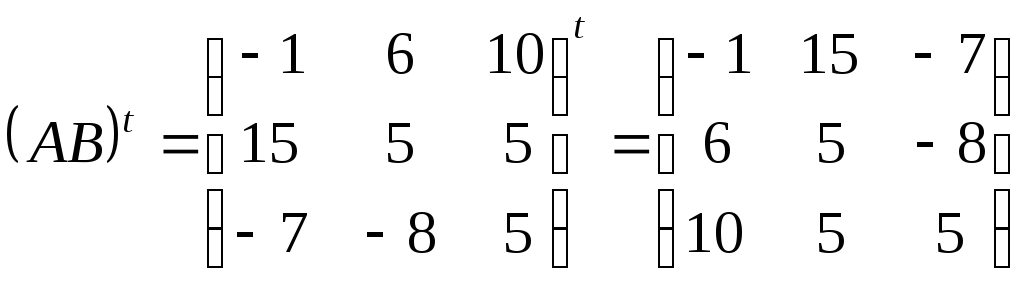 .
.
З іншого боку:
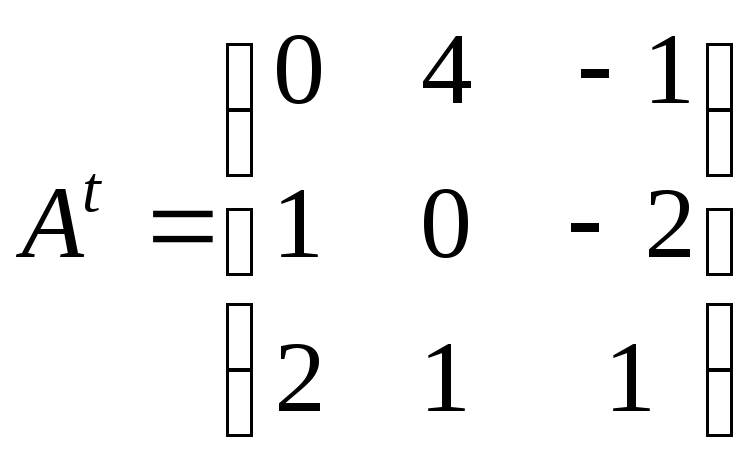 ;
;
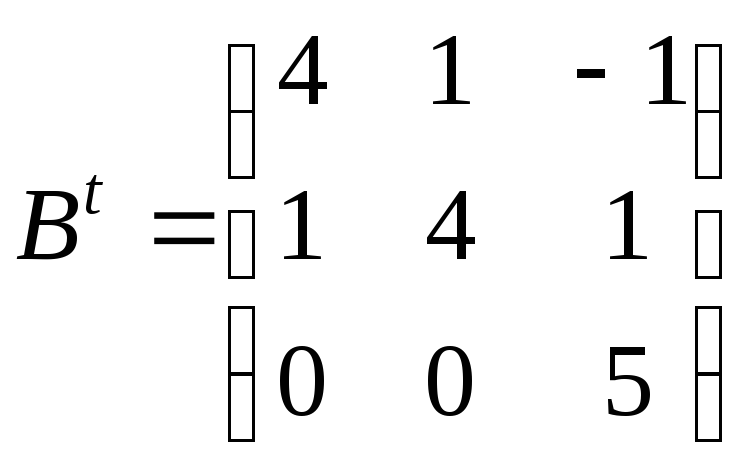 ;
;
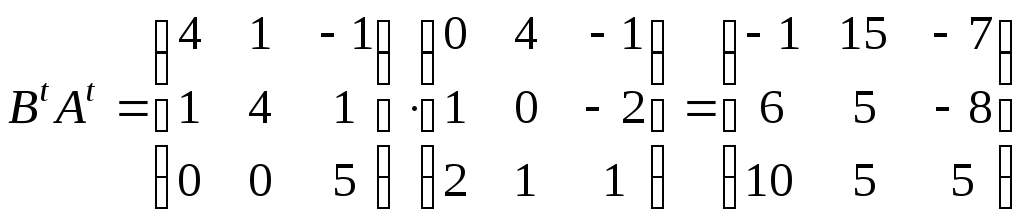 .
.
Рівність вірна.
в) Знайдемо квадрат суми матриць:
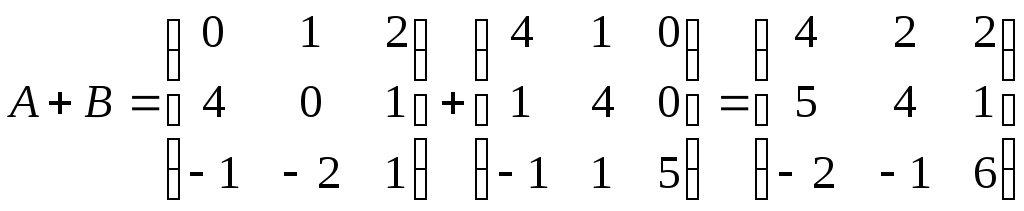 ;
;
 .
.
З іншого боку:
 ;
;
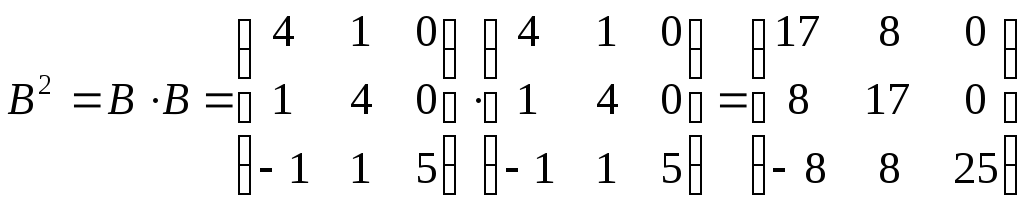 ;
;
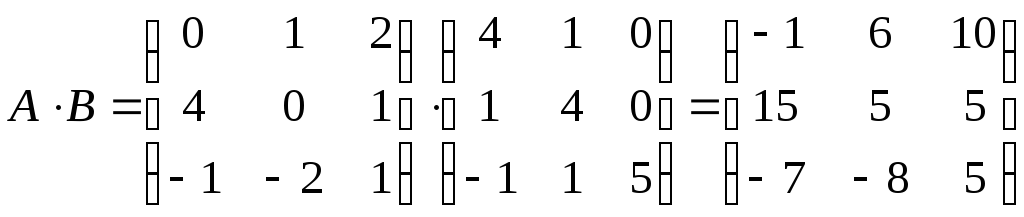 ;
;
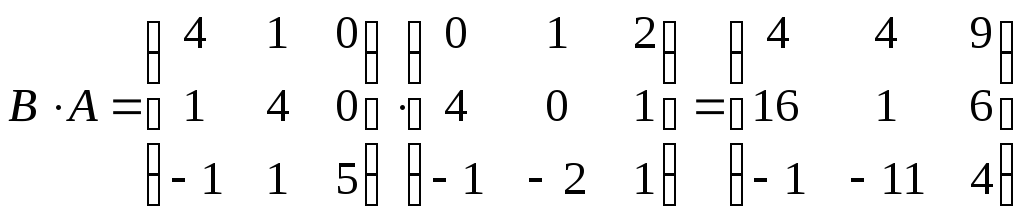 .
.
Таким чином,
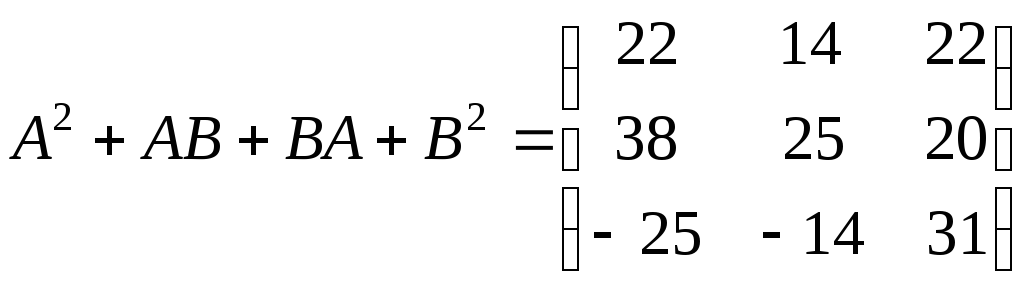 .
.
Отже,
твердження
![]() для даних матриць доведено.
для даних матриць доведено.
Задачі для самостійного розв’язування
Для заданих матриць виконайте зазначені дії:
а)
для матриць
![]() ,
,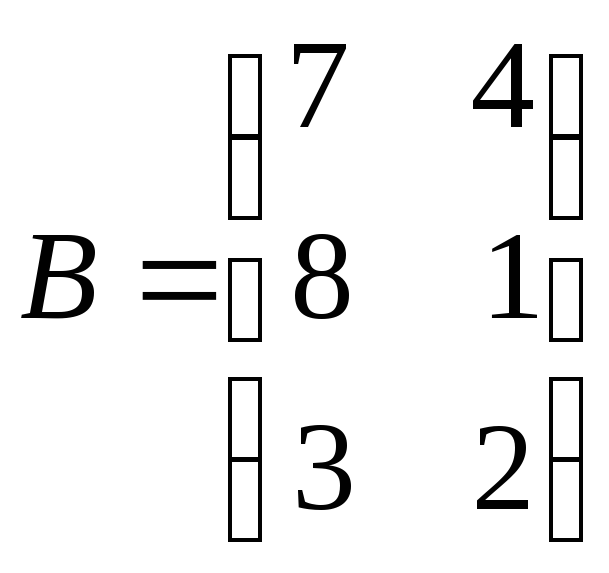 ,
,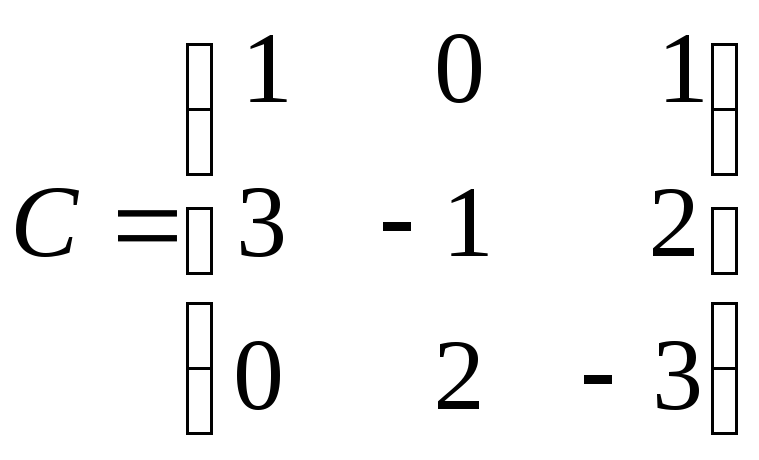 обчисліть
обчисліть![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
б)
для матриць
![]() ,
,![]() ,
,![]() обчисліть
обчисліть![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
в)
для матриць
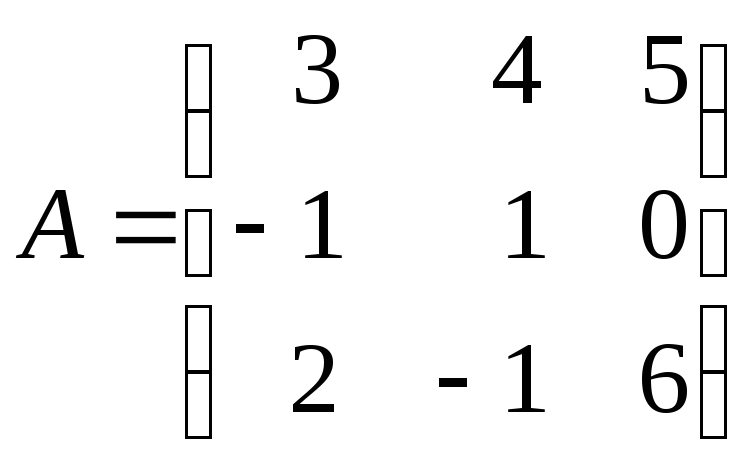 ,
,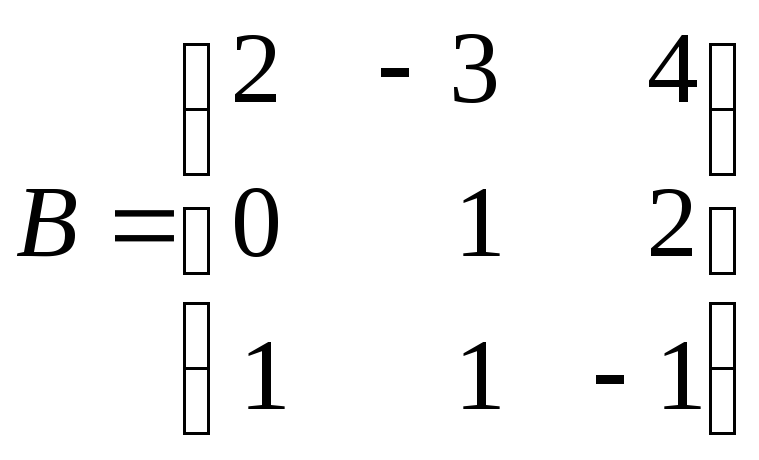 ,
,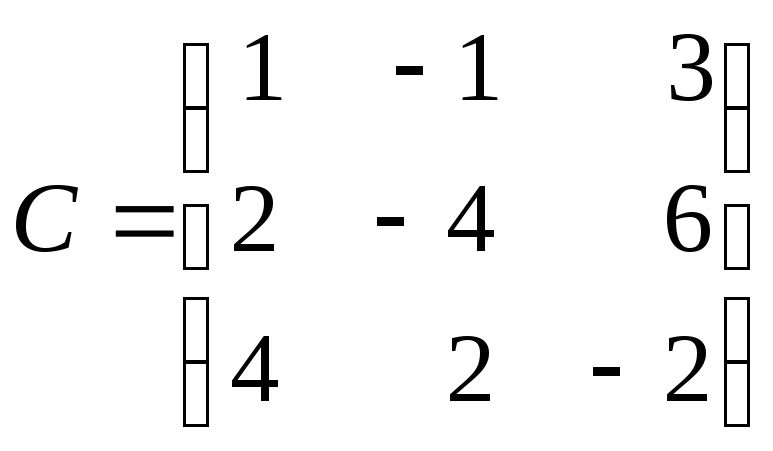 обчисліть
обчисліть![]() ,
,![]() ,
,![]() ,
,![]() .
.
Знайдіть добутки матриць:
а)
![]() ;
б)
;
б)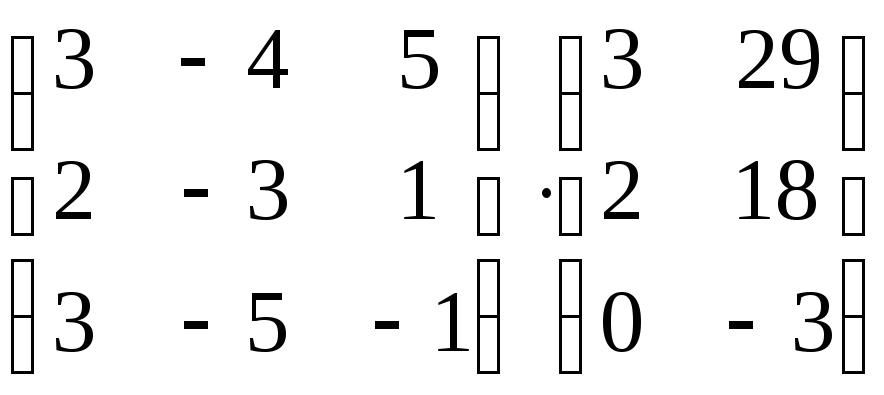 ;
в)
;
в)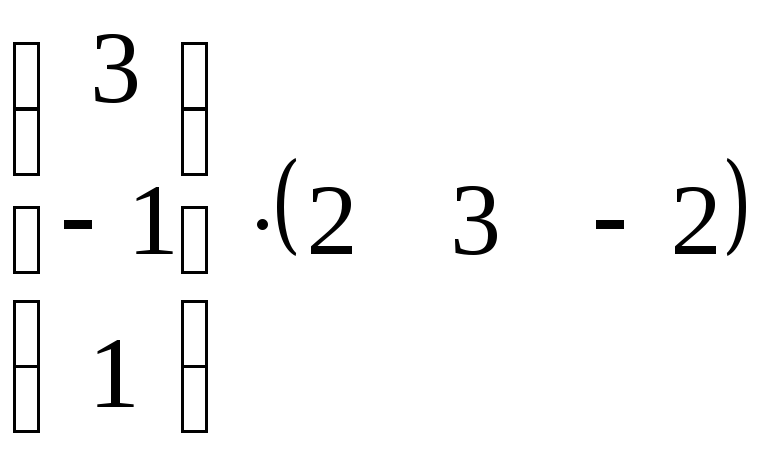 ;
;
г)
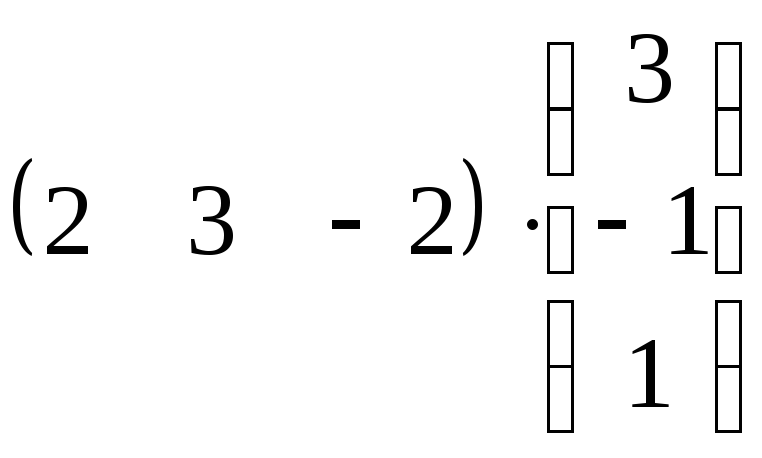 ;
д)
;
д)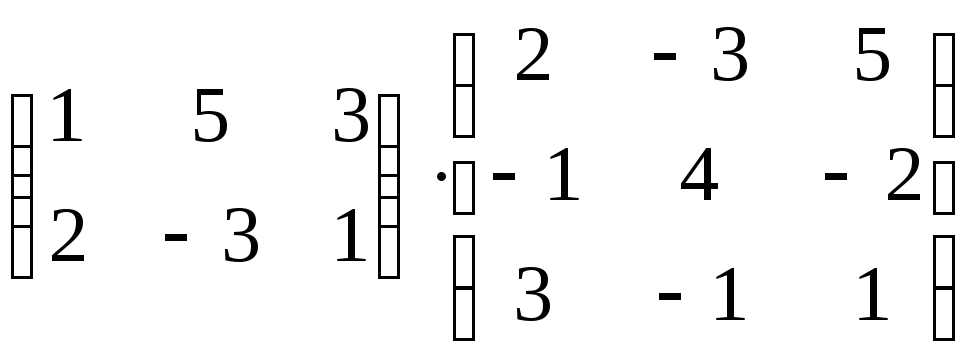 ;
е)
;
е)![]() ;
;
ж)
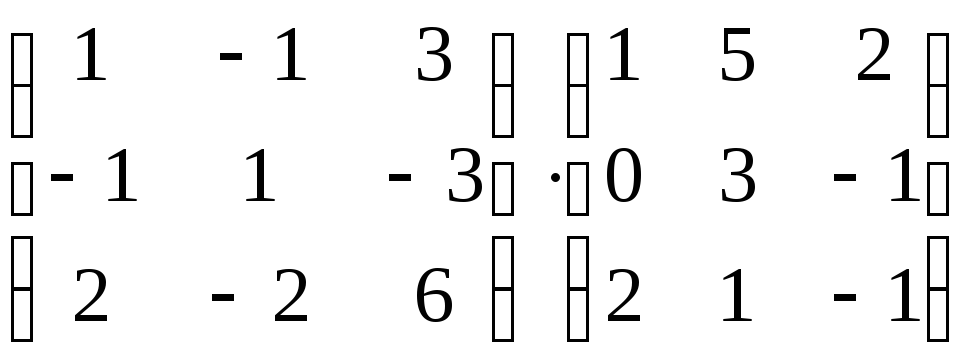 ;
з)
;
з)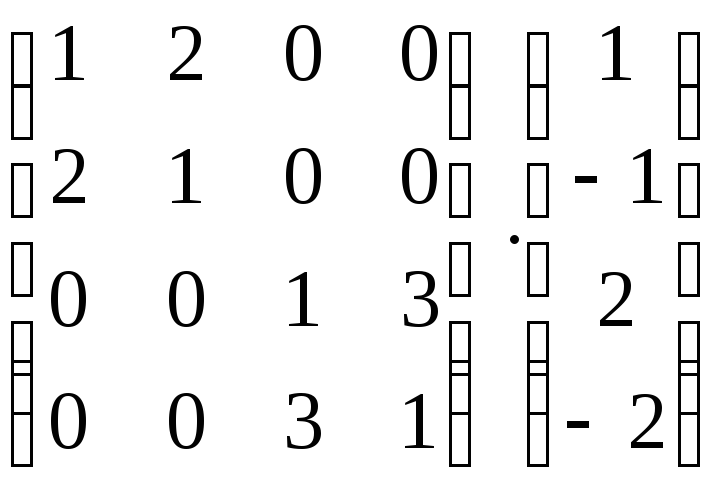 ;
і)
;
і)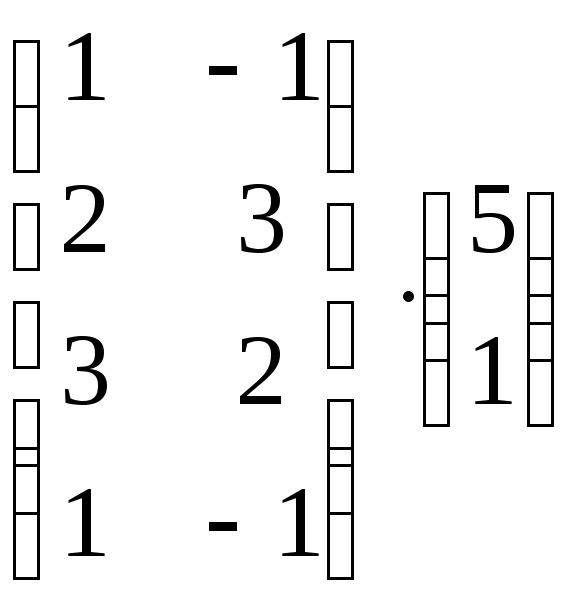 .
.
Обчисліть значення многочлена
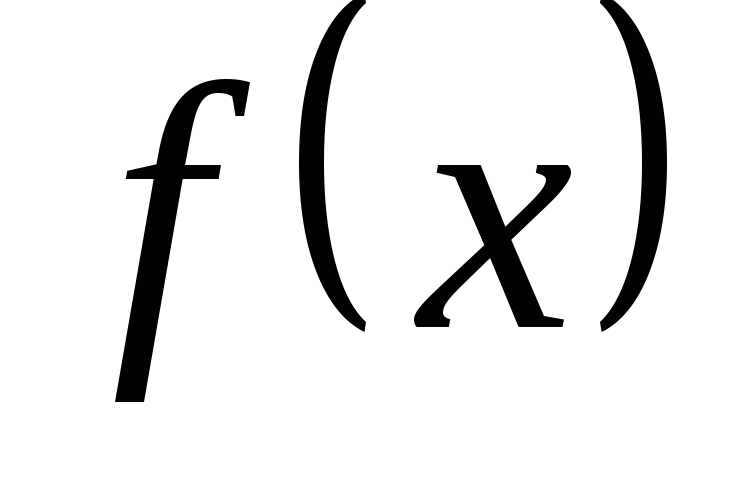 від матриці
від матриці :
:
а)
![]() ,
,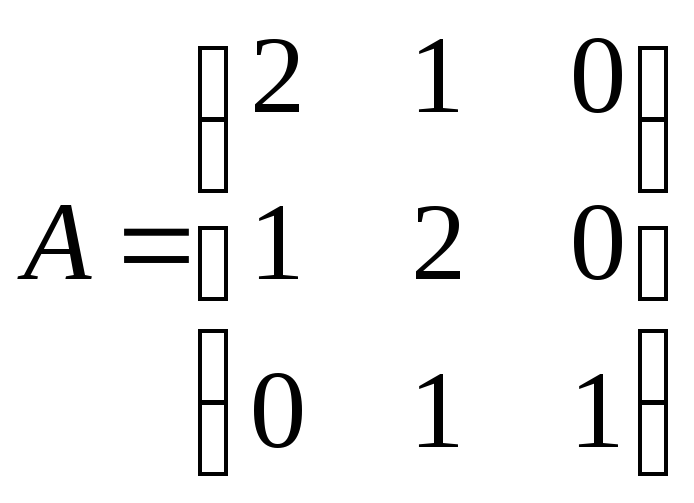 ;
б)
;
б)![]() ,
,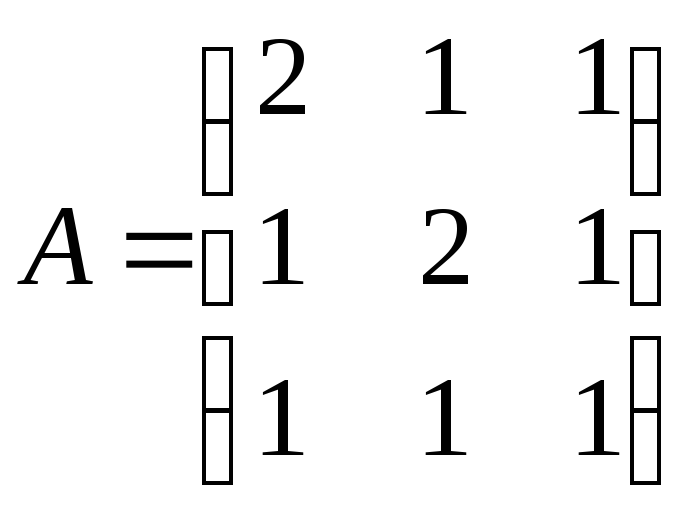 .
.
Зауваження
4.
При знаходженні значення многочлена
![]() від матриці
від матриці![]() будемо вважати його вільний член
будемо вважати його вільний член![]() рівним
рівним![]() ,
де
,
де![]() – порядок матриці
– порядок матриці![]() .
.
Розв’яжіть системи матричних рівнянь:
а)
![]() ,
,![]() ,
,
б)![]() ,
,![]() .
.
Практичне заняття № 2 Тема: Перестановки. Підстановки. Визначник та його властивості
Перестановкою
![]() натуральних чисел
натуральних чисел![]() називається довільний впорядкований
набір цих чисел.
називається довільний впорядкований
набір цих чисел.
Приклад.
Перестановками чисел
![]() є
є![]() ,
,![]() ,
,![]() .
.
Теорема.
Існує
![]() різних перестановок з
різних перестановок з![]() елементів.
елементів.
Інверсією
в перестановці називається пара елементів
![]() таких, що
таких, що![]() та
та![]() перебуває лівіше
перебуває лівіше![]() .
Кількість інверсій у перестановці
.
Кількість інверсій у перестановці![]() позначається
позначається![]() .
.
Приклад.
а)
У перестановці
![]() число 2 утворює інверсію
число 2 утворює інверсію![]() ,
1 не утворює інверсій, 4 –
,
1 не утворює інверсій, 4 –![]() ,
3 та 5 – не утворюють. Отже,
,
3 та 5 – не утворюють. Отже,![]() .
.
б)
Наведемо всі інверсії перестановки
![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() .
Підрахуємо їх кількість:
.
Підрахуємо їх кількість:
![]() .
.
Перестановка називається парною, якщо в ній число інверсій парне, непарною – у противному випадку (див. попередній приклад).
Транспозицією
називається таке перетворення
перестановки, при якому міняються
місцями два елементи перестановки (не
обов’язково ті, що стоять поруч), а всі
інші залишаються на місці. Всі
![]() перестановок з
перестановок з![]() чисел
чисел![]() можна розташувати в такому порядку, що
кожна наступна буде отримуватись з
попередньої однією транспозицією,
причому починати можна з будь-якої
перестановки.
можна розташувати в такому порядку, що
кожна наступна буде отримуватись з
попередньої однією транспозицією,
причому починати можна з будь-якої
перестановки.
Теорема. Будь-яка транспозиція змінює парність перестановки.
Підстановкою
![]() -го
порядку(степеня)
називають
взаємно однозначне відображення множини
-го
порядку(степеня)
називають
взаємно однозначне відображення множини
![]() у себе. Зазвичай підстановки записують
у вигляді матриці розміру
у себе. Зазвичай підстановки записують
у вигляді матриці розміру![]() .
У першому рядку розміщуються елементи
від 1 до
.
У першому рядку розміщуються елементи
від 1 до![]() (прообрази), а в другому рядку – елементи,
в які вони відображаються (образи).
(прообрази), а в другому рядку – елементи,
в які вони відображаються (образи).
Приклад.
Підстановка четвертого порядку
![]() .
.
Підстановка – це дві перестановки, записані одна під іншою у вигляді матриці. Підстановка називається парною (непарною) якщо сума інверсій в обох рядках є числом парним (непарним).
Приклад.
![]() ,
отже підстановка непарна.
,
отже підстановка непарна.
Зауваження. Якщо в підстановці поміняти місцями стовпці, то одержимо іншу форму запису тієї ж підстановки.
Приклад.
![]() .
.
Парність підстановки не залежить від форми її запису.
Приклад.
![]() ,
,![]() .
.
Визначником
(детермінантом) квадратної матриці
![]() порядку
порядку
![]() називається число
називається число![]() (або
(або![]() ,
або
,
або![]() ),
що дорівнює сумі
),
що дорівнює сумі![]() доданків, кожний з яких є добутком
доданків, кожний з яких є добутком![]() елементів цієї матриці, взятих по одному
з кожного рядка та кожного стовпця зі
знаком «плюс», якщо підстановка, складена
з індексів елементів цього добутку,
парна та зі знаком «мінус», якщо непарна.
елементів цієї матриці, взятих по одному
з кожного рядка та кожного стовпця зі
знаком «плюс», якщо підстановка, складена
з індексів елементів цього добутку,
парна та зі знаком «мінус», якщо непарна.
Позначення: при
![]() ,
, ![]() ,
,![]() ;
;
![]() ,
, 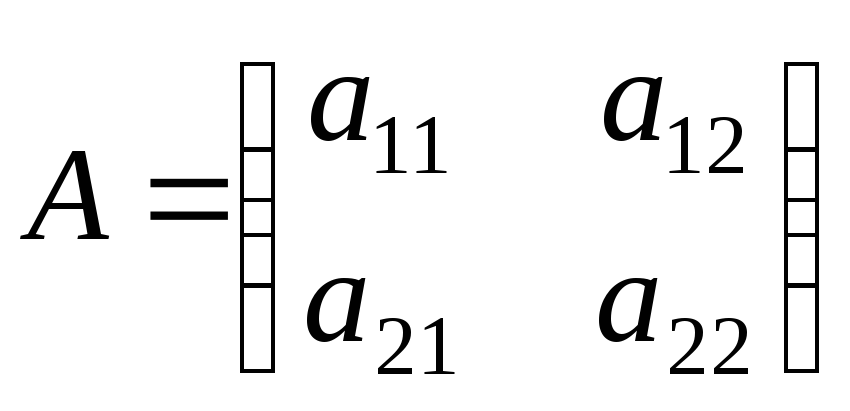 ,
,![]() ;
;
![]() ,
,
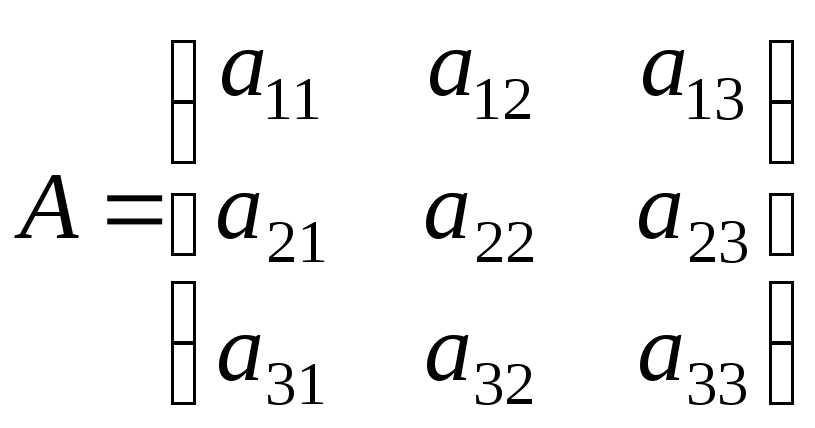 ,
,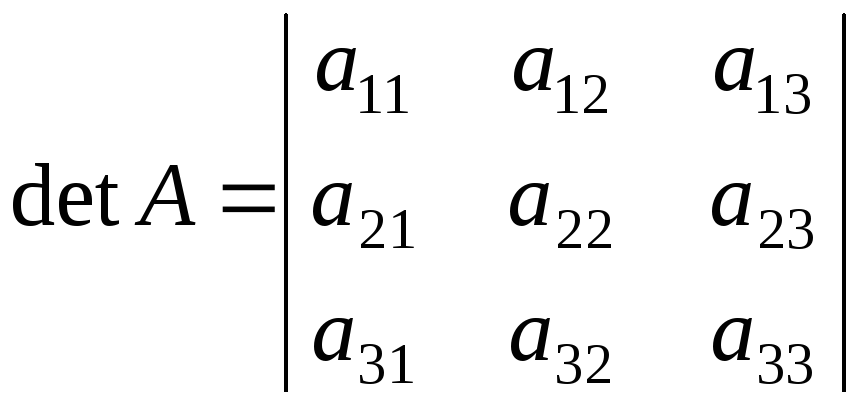 ;
;
…
 ,
, 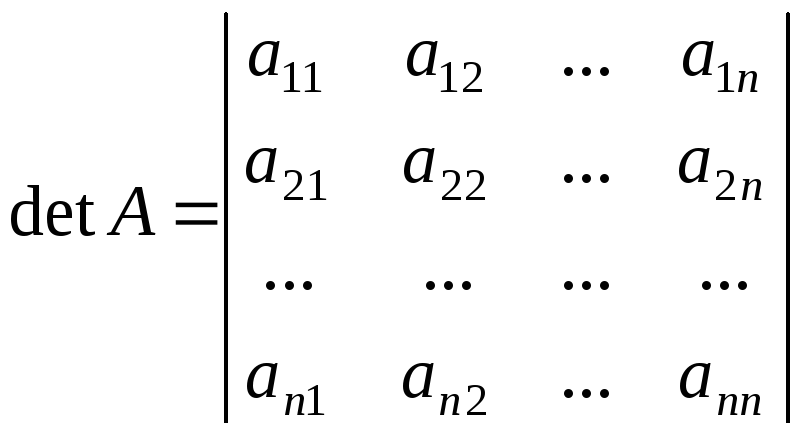 .
.
Означення
детермінанта матриці порядку
![]() ,
з якого випливає правило його обчислення,
є досить складним для сприйняття й
застосування. Однак відомі методи, що
дозволяють обчислити визначники високих
порядків на основі визначників нижчих
порядків.
,
з якого випливає правило його обчислення,
є досить складним для сприйняття й
застосування. Однак відомі методи, що
дозволяють обчислити визначники високих
порядків на основі визначників нижчих
порядків.
Обчислення визначника 2-го порядку ілюструється схемою:
![]()
 .
.
Приклад.
![]() .
.
При обчисленні визначника 3-го порядку зручно користуватися:
правилом трикутників, яке ілюструється схемою:
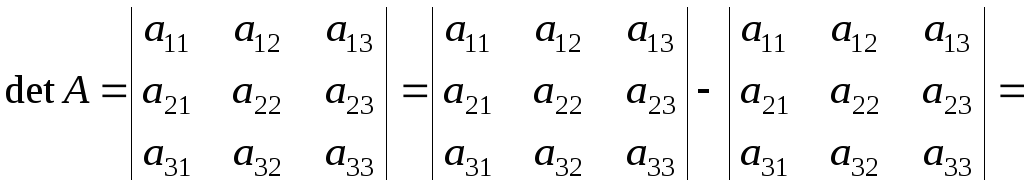

![]() .
.
правилом прямих (правилом Саррюса), яке ілюструється схемою:

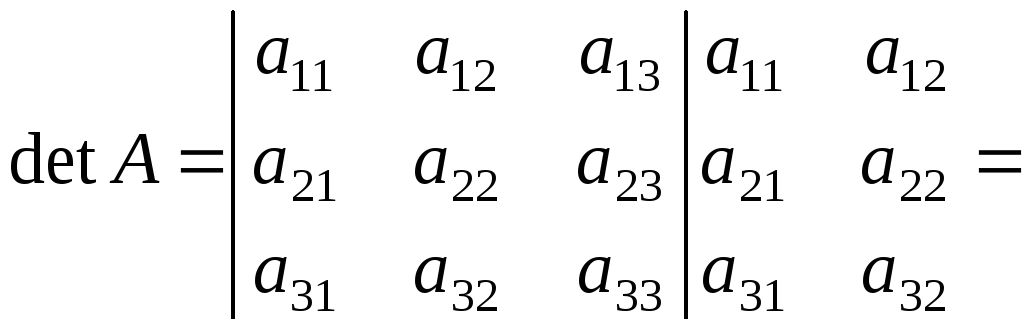
![]() .
.
