
- •Алгебра та геометрія: основи лінійної алгебри
- •Практичне заняття № 1 Тема: Матриці. Дії з матрицями
- •Транспонування матриць
- •Додавання матриць
- •Множення матриці на число
- •Добуток матриць
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 2 Тема: Перестановки. Підстановки. Визначник та його властивості
- •Властивості визначників
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 3 Тема: Методи знаходження оберненої матриці
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 4 Тема: Системи лінійних алгебраїчних рівнянь (слар). Теорема Крамера. Матричний метод розв’язання слар
- •Методи розв’язання слар. Метод Крамера
- •Матричний спосіб розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Практичне заняття № 5 Тема: Ранг матриці. Теорема Кронекера-Капеллі. Метод Гауса розв’язання слар
- •Приклади розв’язування задач
- •Задачі для самостійного розв’язування
- •Завдання для самостійного розв’язування
- •Практичне заняття № 7 Тема: Систематизація та узагальнення знань з розділів лінійної алгебри: «Матриці», «Визначники», «Системи лінійних алгебраїчних рівнянь»
- •Тест для самоперевірки
- •Практичне заняття № 8 Тема: Модульна контрольна робота № 1 (приклад)
- •Завдання для самостійного опрацювання
- •Додаткові завдання для самостійного розв’язування
- •Питання для самоконтролю
- •Індивідуальне завдання
- •Завдання для підвищення рейтингу студента
- •Відповіді
- •Література
- •Додаток а
- •Індивідуальне завдання з курсу «Алгебра та геометрія» за розділом: Основи лінійної алгебри
Практичне заняття № 1 Тема: Матриці. Дії з матрицями
Матрицею
розміру (розмірності)
![]() ,
де
,
де![]() – число рядків,
– число рядків,![]() – число стовпців, називається прямокутна
таблиця з
– число стовпців, називається прямокутна
таблиця з![]() елементів деякої множини. Якщо елементами
матриці є числа, то матриця називається
числовою, якщо вектори, то – векторною,
якщо функції, то – функціональною.
Розглянемо числову матрицю. Місце
кожного елемента
елементів деякої множини. Якщо елементами
матриці є числа, то матриця називається
числовою, якщо вектори, то – векторною,
якщо функції, то – функціональною.
Розглянемо числову матрицю. Місце
кожного елемента![]() матриці однозначно визначається номером
рядка
матриці однозначно визначається номером
рядка![]() й стовпця
й стовпця![]() ,
на перетині яких він знаходиться.
Позначають:
,
на перетині яких він знаходиться.
Позначають:
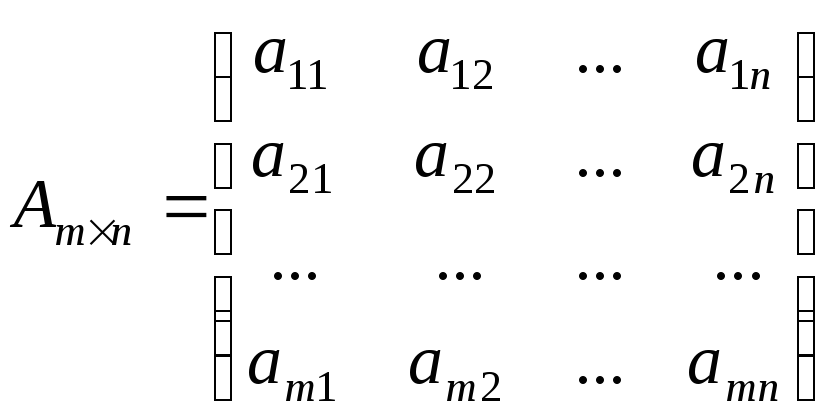 або
або
 ,
,
або
![]() .
.
Матриця,
у якої число рядків дорівнює числу
стовпців, називається квадратною
(квадратну матрицю розмірності
![]() називають матрицею
називають матрицею![]() -го
порядку і позначають
-го
порядку і позначають![]() або
або![]() ).
).
Елементи
![]() ,
,![]() ,
у яких номери рядка й стовпця, на перетині
яких вони знаходяться, співпадають,
утворюютьголовну
діагональ.
,
у яких номери рядка й стовпця, на перетині
яких вони знаходяться, співпадають,
утворюютьголовну
діагональ.
Квадратна матриця, у якої всі елементи, окрім головної діагоналі, дорівнюють нулю, називається діагональною.
Діагональна матриця, у якої всі елементи головної діагоналі дорівнюють одиниці, називається одиничною. Позначають:
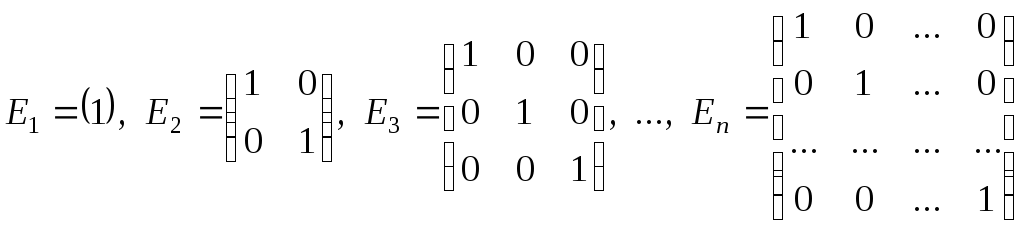 .
.
Квадратна матриця називається верхньотрикутною (нижньотрикутною), якщо всі елементи, розташовані нижче (вище) головної діагоналі, дорівнюють нулю.
Приклад.
Верхньотрикутна
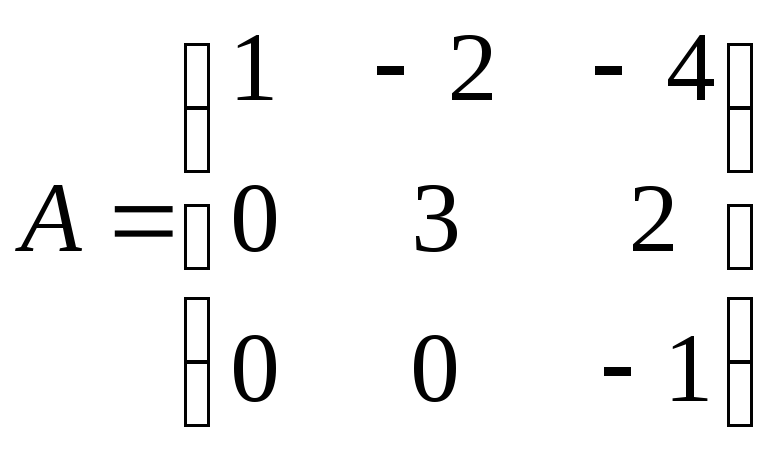 та нижньотрикутна
та нижньотрикутна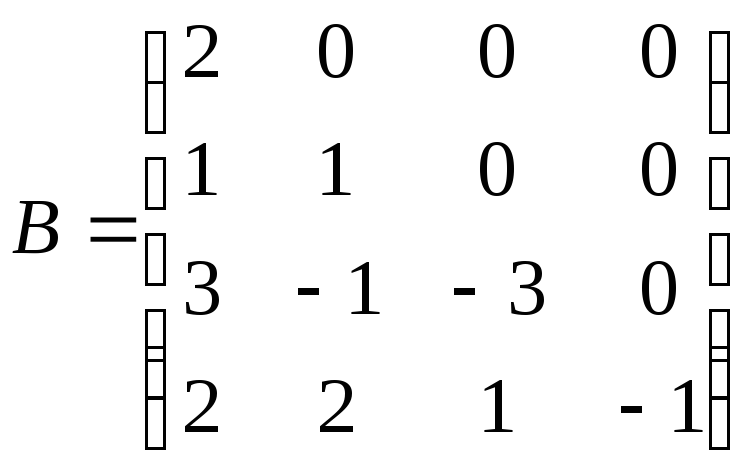 матриці.
матриці.
Квадратна матриця, всі елементи якої дорівнюють нулю, називається нульовою і позначається:
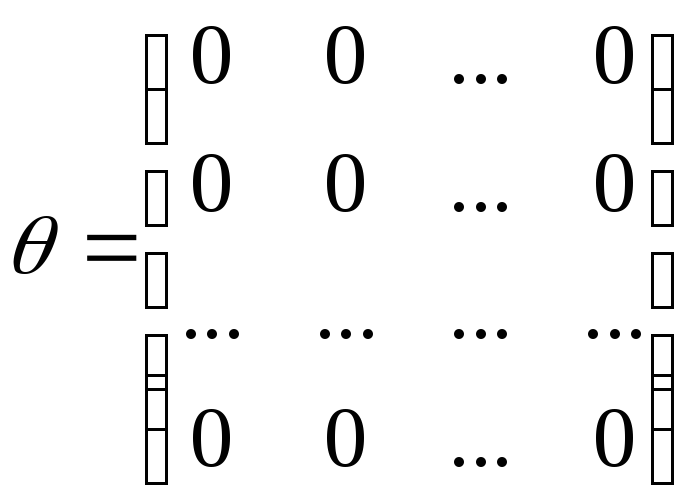 .
.
Матриці
![]() і
і![]() називаютьсярівними,
якщо вони мають однакові розміри й рівні
відповідні елементи, тобто
називаютьсярівними,
якщо вони мають однакові розміри й рівні
відповідні елементи, тобто
![]() ,
якщо
,
якщо
![]() ,
де
,
де![]() ,
,![]() .
.
Якщо
для всіх елементів матриці виконується
умова
![]() (симетрія відносно головної діагоналі),
то матриця називаєтьсясиметричною.
(симетрія відносно головної діагоналі),
то матриця називаєтьсясиметричною.
Приклад.
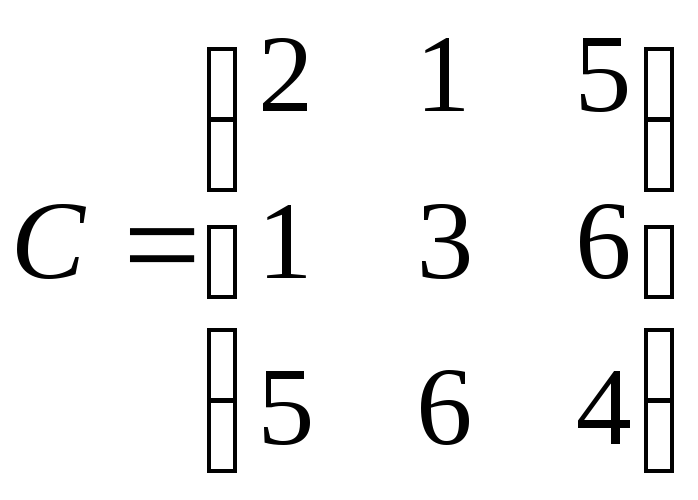 .
.
Матриця, що містить один рядок, називається вектором або матрицею-рядком, а матриця, що містить один стовпець, також називається вектором або матрицею-стовпцем. Їх вид:
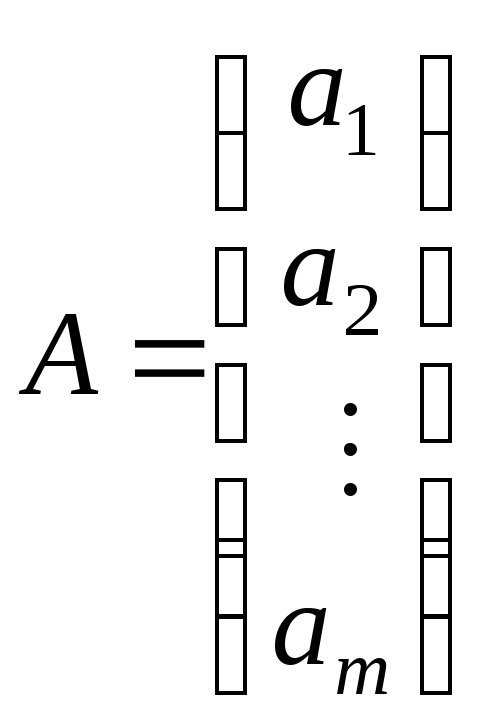 –матриця-стовпець,
–матриця-стовпець, ![]() – матриця-рядок.
– матриця-рядок.
Матриця
розміру
![]() ,
що складається з одного числа, ототожнюється
з цим числом, тобто
,
що складається з одного числа, ототожнюється
з цим числом, тобто![]() є число 5.
є число 5.
Транспонування матриць
Матриця,
отримана з даної заміною кожного її
рядка стовпцем з тим же номером,
називається матрицею, транспонованою
до
даної. Позначають:
![]() або
або![]() .
.
Приклад.
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Транспонування
матриць має таку властивість:
![]() .
.
Додавання матриць
Сумою
двох матриць
![]() і
і![]() однакового
розміру називається матриця
однакового
розміру називається матриця![]() того ж розміру, кожний елемент якої є
сумою відповідних елементів
матриць-доданків, тобто якщо
того ж розміру, кожний елемент якої є
сумою відповідних елементів
матриць-доданків, тобто якщо![]() й
й![]() ,
то
,
то![]() ,
де
,
де![]() ,
,![]() .
.
Приклад.
![]() .
.
Аналогічно
визначається різниця
матриць:
![]() ,
де
,
де![]() ,
,![]() .
.
Множення матриці на число
Добутком
матриці
![]() на
дійсне число
на
дійсне число
![]() називається матриця
називається матриця![]() ,
кожний елемент якої є добутком відповідного
елемента матриці
,
кожний елемент якої є добутком відповідного
елемента матриці![]() та числа
та числа![]() ,
тобто
,
тобто![]() ,
де
,
де![]() ,
,![]() .
.
Приклад.
![]() ,
, ![]() .
.
Матриця
![]() такого ж розміру, що і матриця
такого ж розміру, що і матриця![]() ,
називаєтьсяпротилежною
до матриці
,
називаєтьсяпротилежною
до матриці
![]() ,
якщо
,
якщо![]() .
Наслідком з цього є рівність
.
Наслідком з цього є рівність![]()
Різницю
матриць
![]() можна визначити й так:
можна визначити й так:![]() .
.
Властивості операцій додавання матриць і
множення матриці на число
(![]() – матриці,
– матриці,![]() ):
):
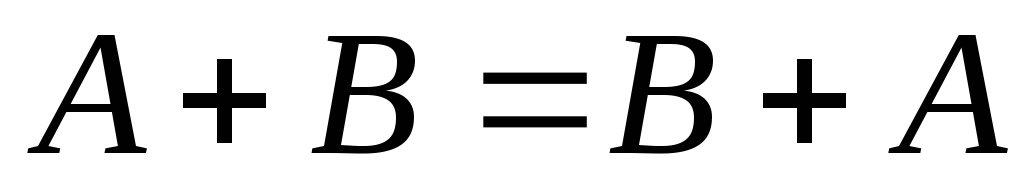 –комутативність
додавання;
–комутативність
додавання;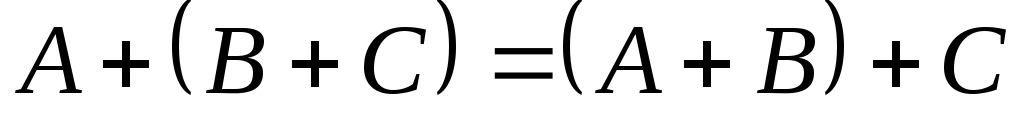 –асоціативність
додавання;
–асоціативність
додавання;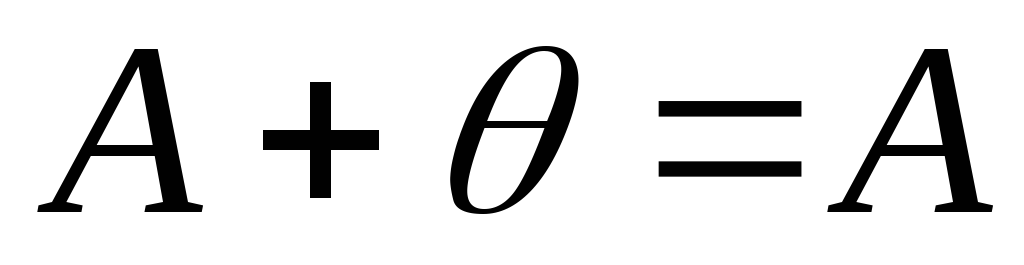 ;
; ;
; 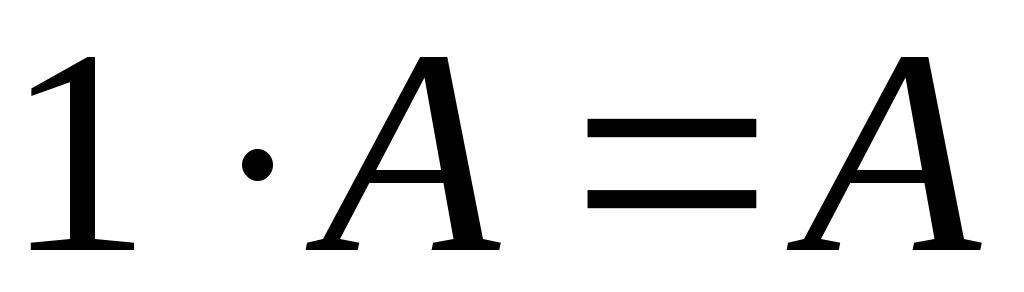 ;
;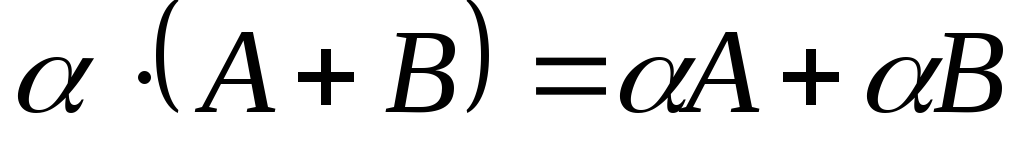 –дистрибутивність;
–дистрибутивність;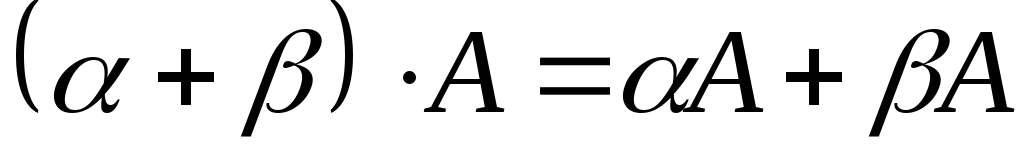 –дистрибутивність;
–дистрибутивність;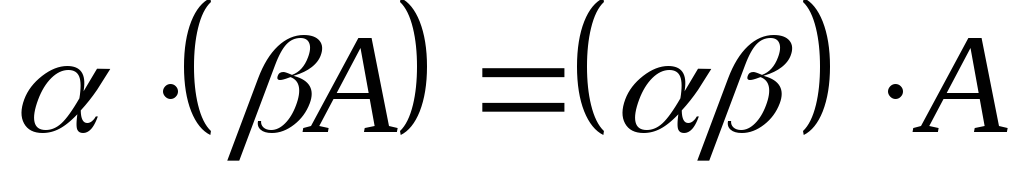 –асоціативність.
–асоціативність.
Добуток матриць
Добутком
матриці
![]() на матрицю
на матрицю![]() називається матриця
називається матриця![]() ,
кожний елемент
,
кожний елемент![]() -ого
рядка й
-ого
рядка й![]() -ого
стовпця якої дорівнює сумі добутків
відповідних елементів
-ого
стовпця якої дорівнює сумі добутків
відповідних елементів![]() -ого
рядка матриці
-ого
рядка матриці![]() та
та![]() -ого
стовпця матриці
-ого
стовпця матриці![]() ,
тобто
,
тобто
![]() ,
де
,
де
![]() ,
,![]() .
.
Зауваження 1. Добуток матриць можливий у випадку, коли кількість стовпців першої матриці дорівнює кількості рядків другої.
Зауваження
2.
Якщо квадратні матриці
![]() й
й![]() одного порядку, то добутки
одного порядку, то добутки![]() й
й![]() завжди існують.
завжди існують.
Приклад.
Знайти добутки
![]() та
та![]() матриць: а)
матриць: а)![]() і
і![]() ;
б)
;
б) і
і![]() .
.
Розв’язання:
а)
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
б)
![]() ,
,
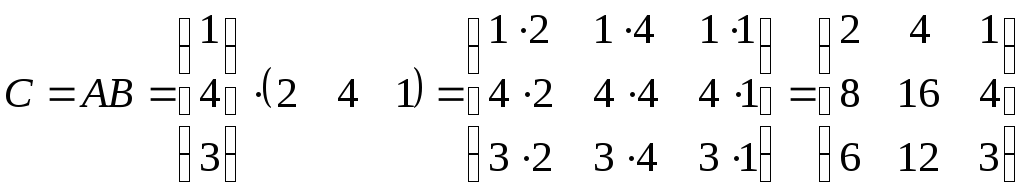 ;
;
![]() ,
,
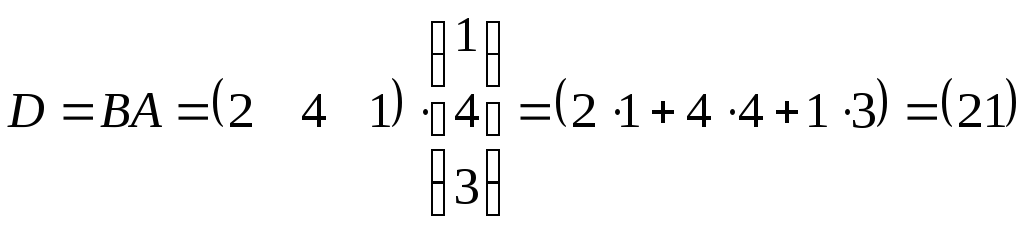 .
.
Зауваження
3.
У загальному випадку добутки
![]() й
й![]() не дорівнюють один одному:
не дорівнюють один одному:![]() .
.
Матриці
![]() та
та![]() називаютьсяпереставними,
якщо
називаютьсяпереставними,
якщо
![]() .
.
Добуток
![]() називається
називається![]() -им степенем матриці
-им степенем матриці![]() .
.
Властивості операцій транспонування, множення,
додавання матриць і множення матриці на число
(![]() – матриці,
– матриці,![]() ),
якщо записані операції мають сенс:
),
якщо записані операції мають сенс:
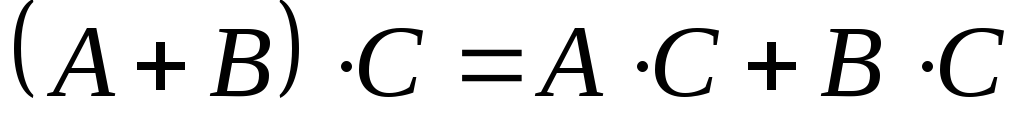 ; 5.
; 5. 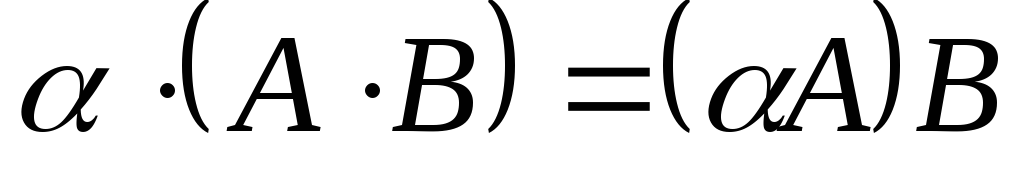 ;
;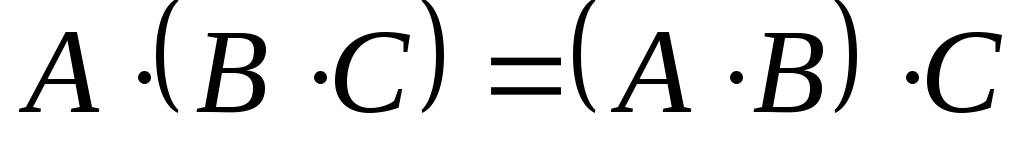 ; 6.
; 6. 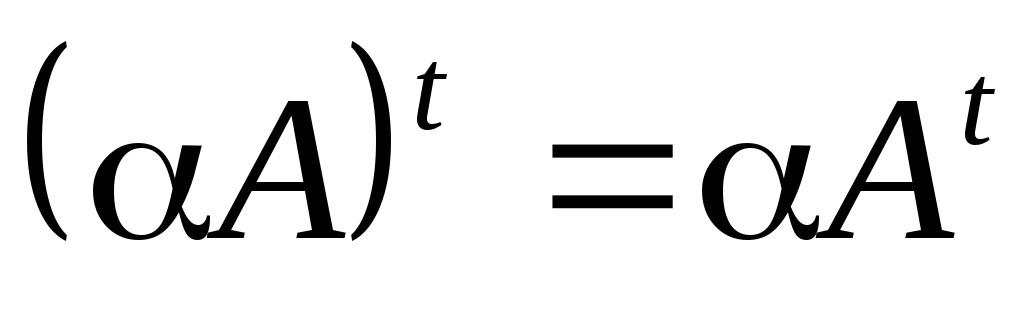 ;
; ; 7.
; 7. 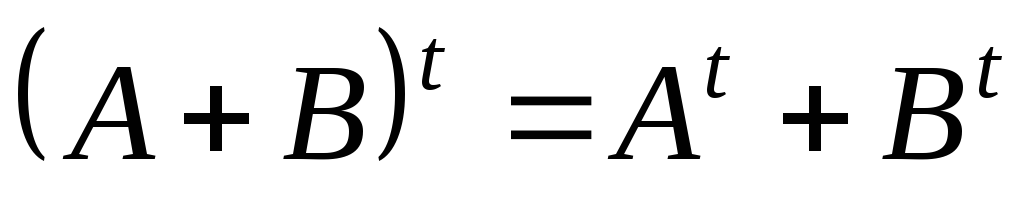 ;
;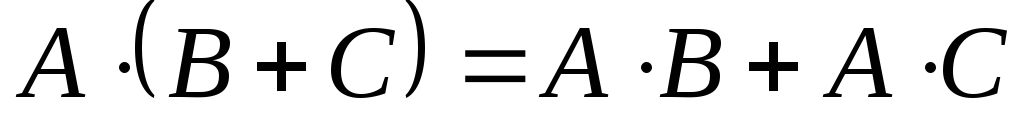 ; 8.
; 8. 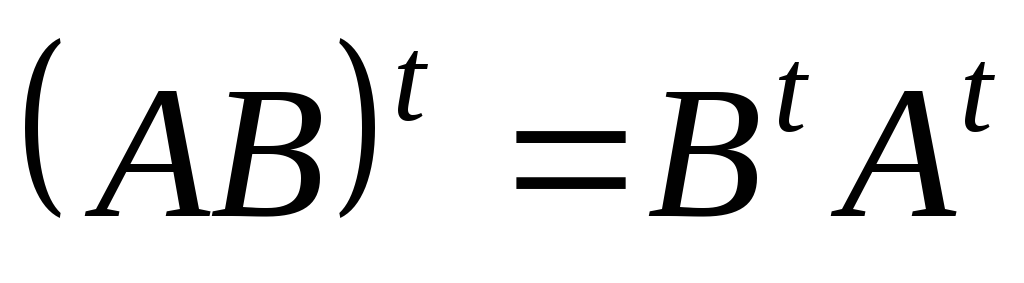 .
.
