• Системи відліку і системи координат. Елементи векторної алгебри

По-перше домовимося про деякі позначення. Векторні величини позначатиме так , модуль того ж вектору - . Середню величину позначатимемо або .

Рух одного тіла і того самого тіла відносно інших тіл можна охарактеризувати по-різному. Для вивчення руху необхідно насамперед обрати тіло або систему нерухомих тіл одне відносно одного, стосовно яких розглядається рух даного тіла або його частини. Опис руху будь-якого тіла має сенс тоді, коли цей рух розглядається відносно іншого тіла або системи тіл, які називають тілом відліку. Оскільки рух відбувається у просторі і в часі, то для повного опису руху тіла потрібно знати розміщення тіла або його частин в будь-який момент часу. Для цього з тілом відліку зв’язують систему координат і годинник, за допомогою якого визначають проміжки часу між двома подіями. Тіло відліку з відповідно зв’язаною системою координат і годинник утворюють єдину систему відліку. Система координат – набір масштабів, за допомогою яких фіксується розміщення рухомих тіл у будь-який момент часу. Розміщенн я тіл можна визначати за допомогою довільної системи координат. На практиці здебільшого користуються прямокутною системою координат. Роль вдалого вибору системи відліку можна показати на такому історичному прикладі: давньогрецький філософ К.Птолемей вважав Землю центром Всесвіту і розглядав рухи планет відносно Землі. Траєкторії руху планет виявилися дуже складними, пояснити цього філософи не змогли. А от коли Н.Копернік обрав тілом відліку Сонце – орбіти планет виявилися близькими до колових – еліпсами з малими ексцентриситетами.

Прямокутна декартова (права) (Мал.0.1) в якій трьома числами (х, y, z), що характеризують положення точки, є довжини х,y,z. Для правої системи поворот від осі до осі в напряму найменшого кута між ними (цей кут показаний вигнутою стрілкою) відбувається в напрямі проти годинникової стрілки, якщо дивитися на площину з верхівки осі .

Циліндрична (Мал.0.2) в якій трьома числами (, ,z), що характеризують положення точки, є довжина , кут  і довжина z. Перехід від циліндричних до декартових прямокутних координат:

, ,

(0.2)

Сферична (Мал.0.3) в якій трьома числами (,,), що характеризують положення точки, є довжина , і кути  і . Перехід від сферичних до декартових прямокутних координат:

, ,

(0.3)

Багато фізичних величин характеризуються одним числом. До них, наприклад, відносяться: температура, маса, енергія, шлях і т.д. Такі величини називаються скалярами. Для характеристики багатьох інших фізичних величин необхідно задати декілька чисел. Фізичні величини, які характеризуються не тільки одним числовим значенням, а і напрямком називаються векторами. Окрім того, складання векторів підкоряється правилу паралелограма. В математиці розглядають вільні вектори (тобто, вектори, які не мають фіксованої точки прикладання).

Вектори спрямовані вздовж паралельних прямих (як одному і тому ж напрямку, так і у протилежних), називають колінеарними. Вектори, які лежать в паралельних площинах, називають компланарними.

Е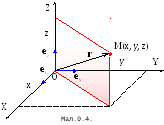 вклідовим простором зветься звичайний тривимірний простір, в якому є справедливими всі п’ять відомих аксіом геометрії Евкліда. Звичайно ми вважатимемо, що в цьому просторі вже існує Декартова права система координат, і ми нею користуватимемося. Будь-яку точку простора з координатами можна з’єднати з початком координат (origin point) спрямованим відрізком, кінець якого лежить в точці, а початок в - origin point. Такий вектор зветься радіус-вектором точки з координатами . Його проекції на осі координат співпадають з координатами точки і дорівнюють . Отже, сукупність точок Евклідового простору і сукупність їх радіус-векторів знаходяться у взаємно-однозначній відповідності. Математики сказали б, що дві ці сукупності є ізоморфними та інфінітними, тобто безкінечними за чисельністю.

Радіусом-вектором точки називатимемо вектор, початок якого співпадає з точкою початку системи координат , а кінець – з точкою що розглядається (Мал.0.4).

, , – одиничні безрозмірні вектори (орти) – базис координатної системи, напрямок яких співпадає з додатнім напрямком осей , , , відповідно:

хyz

(0.4)

де х, y, z – координати радіуса-вектора .

Добутком вектора на число (скаляр) є інший вектор (Мал.0.5), довжина (або модуль, норма) якого в відрізняється від довжини (модуля, або норми) вектора . Якщо проекції вектора на осі координат є , то проекції вектора відповідно є такими: . Нормою, або довжиною вектора (ще інакше цю величину звуть модулем), як відомо, вважається величина:

=

(0.5)

Сумою (різницею) двох векторів (+) називають вектор , який сполучає початок першого вектора () з кінцем другого вектора (). Як видно з Мал. 0.6 та 0.7 сума (різниця) векторів не залежить від порядку додавання.

=+,

(0.6)

С калярним добутком (або лінійною комбінацією) двох векторів і називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними і записують його так:

(,)	(0.7)
Або (,)	(0.7а)

якщо вектори задано своїми декартовими координатами (), (),  – кут між векторами і . Скалярний добуток взаємно перпендикулярних векторів дорівнює нулеві. Окрім того, скалярний добуток є комутативним:

(,)(,)

(0.7б)

В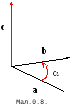екторним добутком [] векторів і називається вектор [], який визначається таким чином: вектори , і складають праву трійку векторів, тобто вектор перпендикулярний до площини, яку утворюють вектори і , і направлений так, що найкоротший поворот від до навколо відбувається проти годинникової стрілки, якщо дивитись з кінця вектора (Мал.0.8). за модулем вектор дорівнює добутку модулів векторів і на синус кута між ними:

	(0.8)
[](–)(–)(–)	(0.9)

Вектори, які є результатом векторного добутку [] і які пов’язані із напрямком обертання мають назву псевдовекторів, або аксіальних. Векторний добуток є не комутативним: []=-[].

Знову умовимося про позначення:

- зростання (приращение – рос.) величини, тобто різниця поміж кінцевим та початковим значенням величини:

=-

(0.10)

(-) - зменшення (убыль – рос.) величини, тобто різниця поміж початковим та кінцевим значенням величини:

-=-

(0.11)

- диференціал (безкінечно мале зростання), наприклад , .

- елементарне значення величини, наприклад - елементарна робота.

Похідна та інтеграл у фізиці мають такий самий, як і у математиці зміст. Найчастіше в різних розділах фізики доводиться брати похідні за часом від функцій часу вигляду , або для векторних величин:

(0.12)

такі величини у фізиці з часів Ньютона позначаються точкою (або декількома точками, якщо мається на увазі похідна вищого порядку) над символом:

(0.13)

Факультет машинобудування
Лектор Дон Н.Л.		стор. 10 з 10