• Рух матеріальної точки. Вектор переміщення

Положення точок у просторі можна характеризувати різними способами, згідно з якими можна описувати і рух точки.

Координатний спосіб опису руху. При русі матеріальної точки відносно системи відліку кожному моменту часу відповідатимуть певні значення її координат. Рух матеріальної точки можна визначити, якщо відома функціональна залежність її координат від часу:

, ,

(1.1.1)

З допомогою функцій (1.1.1) можна обчислити значення координат матеріальної точки для будь-яких моментів часу. Отже, описати рух – значить задати функції (1.1.1).

Лінія, яку описує матеріальна точка в просторі, називається траєкторією руху. Рівняння траєкторії в явній формі можна дістати з системи рівнянь (1.1.1). Якщо траєкторія - пряма лінія, то рух називаютьпрямолінійним; якщо ж це крива лінія, то, рух – криволінійний. Найпростішим прикладом криволінійного руху є рух матеріальної точки по колу. При цьому характер її траєкторії залежить від системи відліку. Так, точки обода колеса, що котиться по горизонтальній площині, матиме різні траєкторії відносно осі обертанні і відносно поверхні площини. У першому випадку це буде коло, у другому – циклоїда. Довжину траєкторії, яку проходить точка за проміжок часу, називатимемо шляхом.

Векторний спосіб опису руху. Положення матеріальної точки в просторі також можна задати за допомогою радіуса-вектора , який проводять з початку системи координат до матеріальної точки. Цей спосіб є більш раціональним. При русі матеріальної точки в загальному випадку величина і напрямз часом змінюються, тобто він є функцією часу:

=

(1.1.2)

У будь-який момент часу проекції радіуса-векторана координатні осі дорівнюють координатам точки. Радіус-вектор через координати точки виражатиме так:

=++

(1.1.3)

д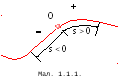е,,- орти, тобто одиничні вектори. При векторному способі опису руху точки одне векторне рівняння (1.1.3) замінює три рівняння (1.1.1).

Опис руху за допомогою параметрів траєкторії. Він застосовується у випадках, коли траєкторія руху є наперед відомою. Якщо траєкторія задана, то завдання зводиться до зазначення закону руху вздовж неї. Деяка точка траєкторії приймається за початкову, а будь-яка інша характеризується відстаннювздовж неї від початкової точки, встановлюється на траєкторії додатній і від’ємний напрямок відліку (як на осі координат) (Мал. 1.1.1).Цей шлях не є вектором, він є скаляром, і не має певного напряму в просторі. В цьому випадку рух описується формулою:

=

(1.1.4)

Вектор переміщення. Розглянемо матеріальну точку, яка в момент часу знаходиться в точці, радіус-вектор якої(Мал. 1.1.2). В момент часу () матеріальна точка буде знаходитись в точці, радіус-вектор якої.

Отже, положення точок таможна задавати радіус-векторами, проведеними з початку координат будь-яких систем відліку. Характерним при цьому є те, що відрізокне залежить від вибору систем відліку.

В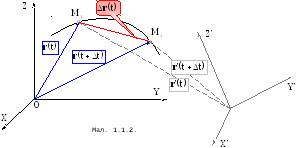ідрізок, що характеризує зміну положення матеріальної точки і має напрям від початкового до наступного її положення, називатимемовектором переміщення:

=-

(1.1.5)

Через відповідні зміни координат рухомої точки вектор переміщення має вигляд:

=++

(1.1.6)

Криву, яку описує кінець радіус-вектора під час руху матеріальної точки, називають годографом. Отже, траєкторія руху матеріальної точки є годографом радіус-вектора . Модуль вектора переміщення в загальному випадку не збігається з довжиною ділянки траєкторії між цими точками. Такій збіг може бути у випадку прямолінійного руху. При русі точки по колу за час, що дорівнює періоду обертання, вектор переміщення дорівнює нулю, а довжина траєкторії – довжині кола.

Всі тіла при певних умовах деформуються, тобто змінюють свою форму. Введемо таку модель: тіло, яке при будь-яких умовах не зазнає деформації називатимемо його абсолютно твердими. У таких тілах відстань між точками, точніше між двома його частинами, залишається сталою. Якщо під час руху форма тіла не змінюється або зазнає незначних змін, його рух можна розглядати як рух абсолютно твердого тіла.

Будь-який складний рух абсолютно твердого тіла можна розкласти на два простих механічних рухи – поступальний і обертальний. Поступальним рухом тіла називатимемо такий рух, при якому пряма лінія, яка з’єднує будь-які точки тіла, з часом залишається паралельною сама собі, тобто її орієнтація у просторі не змінюється. При поступальному русі (один з найпростіших) переміщення всіх його точок однакові. Тому, знаючи рух будь-якої точки тіла, ми можемо визначити рух всіх інших його точок.

Обертальним рухом називатимемо такий рух, при якому траєкторії всіх точок тіла – це концентричні кола з центром на одній прямій, яку називатимемо віссю обертання. При обертальному русі вісь обертання може знаходитись за межами тіла, що здійснює обертальний рух, а може проходити через нього. Обертання тіла навколо осі можна розкласти на поступальний рух і обертання його навколо іншої осі.

Рух твердого тіла називатимемо плоским, якщо будь-яка точка тіла залишається в одній із паралельних площин.