• Системи тотожних квантових частинок: бозони та ферміони. Ефект бозе-конденсації та принцип заборони Паулі для ферміонів

Якщо квантові системи складаються з однакових частинок, то в них спостерігаються специфічні явища, яким немає аналогій в класичній механіці. Квантово-механічний принцип неможливості розрізнення тотожних частинок можна сформулювати у термінах векторів стану. Припустимо, що - вектор стану найпростішої системи з двох тотожних частинок, причому символи означає повний набір координат та квантових чисел, включно із спіновими, для першої та другої частинок системи. Тотожність частинок потребує, щоби після перестановки їх місцями, квантовий стан, отже й густина ймовірності не змінилися:

(5.5.9)

(5.3.1)

З (5.5.9) випливають лише дві можливості, або:

(5.5.10)

(5.3.1)

тобто перестановка частинок взагалі не змінює вектору стану, такі системи називатимемо системами у симетричному (щодо парних перестановок) стані, або ж :

(5.5.11)

(5.3.1)

тобто вектор стану змінює знак після кожної перестановки, такі системи називатимемо такими, що перебувають в антисиметричному стані.

Оскільки лише суперпозиції функцій однакової симетрії можуть мати властивість (5.5.10), або, навпаки, (5.5.11), симетрії або антисиметрії, то принцип суперпозиції вимагає аби всі можливі стани кожної з систем тотожних частинок були або станами типу (5.5.10), тобто симетричними, або станами типу (5.5.11), тобто антисиметричними. Таким чином, всі квантові частинки можна поділити на два вичерпні класи: ті, що мають симетричний системний вектор стану – бозони, і те, котрі мають антисиметричний системний вектор стану – ферміони. Причому належність частинок до кожного з класів зберігається в часі: електрон завжди є ферміоном, тоді як фотон – завжди бозон.

Поміж бозонами та ферміонами спостерігаються також інші відмінності. Спінові моменти бозонів є цілими (можливо, навіть нульовим) відносно сталої Планка: отже , тоді як для ферміонів спін ніколи не буває нульовим і завжди є напівцілим відносно : отже . Це емпіричне правило є постулатом в нерелятивістській квантовій механіці. Зокрема, ферміонами серед квантових частинок є всі частинки з груп лептонів, баріонів та кварків. Тоді як всі фотони, проміжкові векторні бозони, мезони та глюони. Складні квантові частинки (наприклад, атомні ядра) можуть бути як ферміонами так і бозонами.

Розглянемо два не взаємодіючих поміж собою ферміони. Якщо стани кожної з частинок абсолютно однакові (частинки мають однакові набори квантових чисел, наприклад) тоді їх перестановка не повинна змінювати системного вектора стану, тобто стан такої „квантової системи” мусить бути симетричним. Зрозуміло, що ми назвали два таких ферміони „системою” дещо штучно, насправді вони не є системою, доки не взаємодіють поміж собою.

Проте, якщо ферміони почнуть взаємодіяти поміж собою, тобто утворять справжню квантову систему з двох тотожних частинок, то системний вектор стану повинен бути антисиметричним і міняти знак при перестановці ферміонів. Звідси виникає висновок, що пара взаємодіючих ферміонів, які складають квантову систему, не можуть, на відміну від двох непов’язаних ферміонів, перебувати в ідентичних квантових станах (зокрема, мати однакові всі квантові числа). Ця властивість ферміонних квантових систем має назву принципу заборони Паулі. Він розповсюджується на всі ферміонні квантові системи з довільним числом тотожних частинок.

Принцип Паулі заборони ідентичних квантових станів для ферміонних систем, зрозуміло, не розповсюджується на бозонні системи, оскільки їх системний вектор стану є симетричним щодо перестановок частинок. Навпаки, в бозонних квантових системах спостерігається протилежне явище: при низьких температурах більшість, або всі бозони системи переходять в основний, найнижчий за енергією можливий квантовий стан. Квантові стани всіх, або майже всіх бозонів стають ідентичними. Такий ефект отримав назву низькотемпературної конденсації бозонів (або, іншими словами, утворення бозе-конденсату).

На рис.3 показана експериментально досліджені деталі поведінки двох квантових систем в діапазоні надзвичайно низьких температур . Зниження температури призводить до інтенсивної конденсації бозонної хмарки, тоді як відстань поміж ферміонами в системі змінюється значно слабкіше.

Табл.1 Деякі відмінності поміж квантовими системами тотожних частинок

Клас частинок	Поведінка системного вектору стану при перестановці пари тотожних частинок (i,j)	Спін	Особливості квантових систем тотожних частинок
Бозони	симетричний стан	Цілий	Бозе-конденсація
Ферміони	антисиметричний стан	Напівцілий	Принцип заборони Паулі

Рівняння Шредінгера для атома водню. Енергетичний спектр електрона в атомі водню

„Хотілося б думати, а дехто дійсно так думає, що хвильова механіка дає загалом рішення всіх теоретичних проблем хімії та фізики. Втім у дійсності це не так” (К. Дей, Д.С. Селбін. Теоретична неорганічна хімія,М.:Хімія,1976,с.53). Тим більш цінними є квантові задачі, які мають точні, або майже точні, і, головне, аналітичні рішення, до яких належить, зокрема, і задача про рух електрона в атомі водню.

Насамперед погодимося вважати силове поле ядра, в якому рухається електрон, сферично симетричним. Для цього доведеться вважати ядро нерухомим силовим центром, розташованим на початку координат. І хоча насправді це не зовсім вірно, оскільки ядро, як і електрон рухається навколо спільного центра мас, велика різниця мас електрону та ядра () дозволяє вважати рухомим лише електрон. Виправлення, які необхідно зробити для урахування також і руху ядра, ми зробимо пізніше.

Якщо поле ядра вважається сферично симетричним, то, по-перше, для руху електрону в полі ядра повинні виконуватися закони збереження характерні для руху квантової частинки в таких полях, тому зберігаються в часі повна механічна енергія електрону, квадрат моменту імпульсу та його проекція на полярну вісь і до того ж проекція спінового моменту . По-друге потенційна енергія взаємодії електрону та ядра в атомі водню повинна залежати лише від відстані поміж цими частинками, і з закону Кулона маємо:

(5.6.1)

(5.3.1)

де - електрична стала, - заряд ядра воднеподібного атому (іону). Для атомарного водню, зрозуміло, . Силова функція (потенційна енергія) (5.6.1) стаціонарна, тому що не залежить від часу явно, через що квантові стани електрона в атомі водню є також стаціонарними.

Нарешті, як було показано раніше при вивченні загальних особливостей руху в сферично симетричних полях, у сферичній системі координат вектор стану електрону можна записати як добуток двох функцій, радіальної та сферичної:

(5.6.2)

(5.3.1)

Стаціонарне рівняння Шредінгера, якому задовольняє функція (5.6.2) у системі координат можна записати так:

(5.6.3)

(5.3.1)

Оператор Лапласа в сферичній системі координат виглядає так:

(5.6.4)

(5.3.1)

Підстановка (5.6.4) та (5.6.2) у (5.6.3) дозволяє знайти фактори в правій частині виразу (5.6.2) тобто радіальну та сферичну функції (фактори вектора стану) електрону з двох незалежних рівнянь на котрі розпадається рівняння (5.6.3).

Важливим фактом є те, що рівняння (5.6.3) має ненульові рішення не при довільних значеннях параметру . Насамперед можна показати, що такі рішення існують лише при будь-якому значенні . При виконанні цієї умови енергетичний спектр електрону є суцільним і асимптотичне (при )співпадає із спектром вільної частинки. Отже, випадок відповідає нелокалізованому, відірваному від ядра і здійснюючому інфінітний рух, фактично вільному, електрону.

Дискретний спектр електрону існує лише при умові . За такої умови квантова теорія дає вираз, аналогічний простій теорії Бора:

(5.6.5)

(5.3.1)

де - головне квантове число.

Виправлення, пов’язані з рухом ядра дещо змінюють вираз для енергії (5.6.5). Праву частину виразу (5.6.5) треба помножити на фактор

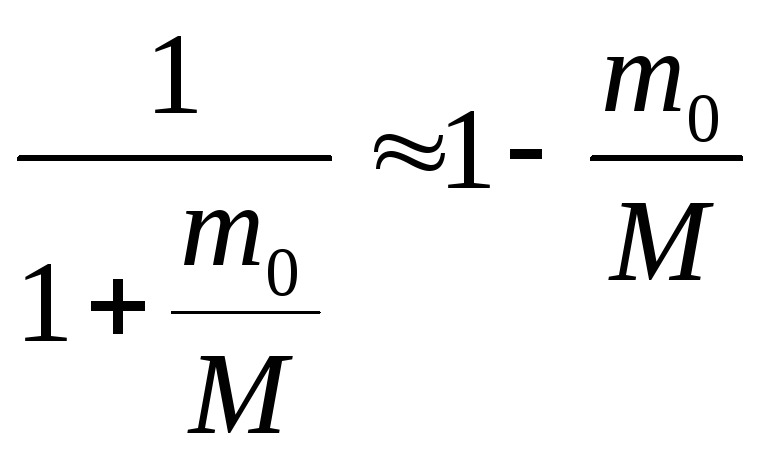(5.6.6)

який передбачає, що з урахуванням руху ядра у виразі (5.6.5) повинна фігурувати так звана приведена маса двох частинок замість маси електрону . Проте чим сильніше відрізняються маси та , тим точніше виконується наближена рівність .