• Закони Ома та Джоуля-Ленца в диференціальній формі. Закон Ома для неоднорідного провідника

Закон Ома в диференціальній формі можна отримати з (3.4.2), якщо врахувати, що

(3.4.8)

де - середній час вільного пробігу носія струму від зіткнення до зіткнення; - його заряд та маса. Підставляючи (3.4.8) у (3.4.2) маємо наступний вираз для закону Ома:

(3.4.9)

де через

(3.4.10)

позначено так звану питому провідність провідника.

Густина енергії , яку передає в одиниці об’єму провідника носіїв струму за рахунок зіткнення з іншими частинками за проміжок часу , дорівнює роботі електричного поля з переміщення цих зарядів:

(3.4.11)

Останній вираз є законом Джоуля-Ленца в диференційній формі. Його інколи записують у наступному вигляді:

(3.4.12)

трактуючи величину як густину потужності електричного струму – потужність, яка виділяється в одиниці об’єму провідника.

Від виразів (3.4.9) та (3.4.12) легко перейти до відомих інтегральних форм законів Ома та Джоуля-Ленца для однорідної ділянки електричного кола:

(3.4.13)

де - так звана провідність, обернена пропорційна електричному опору ділянки ; - площа перерізу та довжина провідника. Опір провідника в СІ вимірюють в омах (Ом): =Ом, а провідність – в сименсах (См).

Формула (3.4.13)виражає в інтегральній формі закон Ома для ділянки однорідного кола. Ділянку кола називають однорідною, якщо на ній немає джерел струму. Закон Ома справджується з великою точністю для металевих провідників та електролітів. Відхилення від закону Ома становить близько 1% для струмів дуже великої густини – кількох мільйонів ампер на 1 см². закон порушується і в тих випадках, коли в провідниках не вистачає носіїв електричних зарядів і настає насичення струму (несамостійний розряд у газах), а також при досить високих напругах ат ін. Залежність = називають вольт-амперною характеристикою провідника.

– (закон Джоуля-Ленца)

(3.4.14)

де - потужність електричного струму на однорідній ділянці.

Якщо електричне коло є неоднорідним, тобто містить в собі джерела ЕРС, як на Мал.3.4.2, то закон Ома в інтегральній формі звичайно записують у дещо іншій формі:

(3.4.15)

де - еквівалентний опір зовнішнього кола (ланцюга), приєднаного до джерела ЕРС, - внутрішній опір самого джерела.

(3.4.16)

Проте з закону Ома для ділянки кола (3.4.14) відомо, що - падіння напруги (напруга) на зовнішньому опорі кола. Отже, - падіння напруги на внутрішньому опорі джерела.

ЕРС дорівнює сумі падінь напруги на зовнішньому та внутрішньому опорі кола.

• Електричний опір. Правила з’єднання провідників

Електричний опір металів зв’язаний з розсіянням електронів провідності на теплових коливаннях кристалічної решітки і структурних неоднорідностях.

Зауважимо, що опір провідника в першому наближенні не залежить від сили струму, який проходить по провіднику, а залежить від його геометричних розмірів, форми та від матеріалу провідника і його стану. Для однорідних провідників циліндричної форми:

(3.4.17)

де - довжина провідника, - площа поперечного перерізу, - коефіцієнт пропорційності, який залежить від матеріалу та фізичного стану провідника. Його називають питомим опором матеріалу. Одиницею виміру в СІ є ом на метр: = Ом.м.

Питомий опір провідників значною мірою залежить від домішок, а також від способу виготовлення провідників. Найменший питомий опір мають срібло і мідь. На практиці для передавання електричної енергії використовують дріт із міді або алюмінію. Для виготовлення реостатів, котушок опору використовують сплави з великим питомим опором (ніхром, нікелін).

Як уже зазначалося питомий опір провідників залежить не лише від хімічного складу речовини, а й від його стану, зокрема температури. Залежність питомого опору однорідної речовини від температури характеризують температурним коефіцієнтом опору :

(3.4.18)

Температурний коефіцієнт опору чисельно дорівнює відносній зміні опору провідника при зміні його температури на 1 К. Величина для різних речовин різна. Для всіх чистих металів близький до 1/273 К^-1. Він також може дещо змінюватися при зміні температури даної речовини. Деякі сплави мають досить малі значення , наприклад, для константану =0,1*10^-4К^-1. дріт із таких сплавів використовують для виготовлення еталонів опору, котушок вимірювальних місткових схем тощо.

Як показують досліди, для кожного хімічно чистого металевого провідника існує певний інтервал температур, в якому залежність питомого опору від температури має лінійний характер, тобто:

=(1+)

(3.4.19)

де - питомий опір, що відповідає початку температурного інтервалу. Здебільшого за початок цього інтервалу беруть температуру С. Залежність опору металів від температури покладено в основу роботи приладів для вимірювання температури (термометри опору), енергії випромінювання (болометри) та автоматичних пристроїв для термостатування, терморегулювання будь-яких процесів з великою точністю.

Розглянемо різні способи з’єднання провідників у колі.

На Мал.3.4.3. показано послідовне з’єднання опорів. при такому з’єднанні загальне падіння напруги дорівнює сумі падінь напруги на кожному резисторі (), через кожен з резисторів тече однаковий струм , а їх загальний опір дорівнює сумі опорів резисторів:

(3.4.20)

На наступному Мал.3.4.4. показано паралельне з’єднання провідників (резисторів). В цьому випадку однаковою є напруга на всіх резисторах і на кожному з них (); сила струму на „вході” та „виході” ( до точки розгалуження А і після точки В) є сумою сил струмів, що течуть по кожному резисторові ( ); а загальний опір знаходять з формули:

(3.4.21)

Розглянемо тепер способи з’єднання джерел струму.

Почнемо з послідовного з’єднання, коли з’єднують різнойменні полюси, як на Мал.3.4.5. У такому випадку сумарна ЕРС є просто сумою ЕРС кожного джерела, а їх внутрішні опори також сумуються:

	(3.4.22)

При такому способі з’єднання ми виграємо в електрорушійній силі, але збільшуємо внутрішній опір складного джерела.

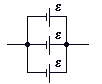Не набагато складнішою є ситуація паралельного з’єднання джерел струму, яка показана на наступному Мал.3.4.6. Розглянемо лише випадок, який найчастіше застосовують на практиці – декілька однакових ЕРС, з’єднаних паралельно. В такому випадку повна ЕРС дорівнює - електрорушійній силі кожного з джерел, а загальний внутрішній опір зменшується в три рази, якщо в ній покласти всі три опори однаковими. Отже, при такому з’єднанні ми не виграємо в ЕРС, але в декілька разів зменшуємо внутрішній опір складного джерела струму.