Лабораторна робота № 5–1

Лабораторна робота № 5-1

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В’ЯЗКОСТІ РІДИНИ

Мета роботи: вивчення процесів руху тіл у рідині та явища внутрішнього тертя у реальних рідинах.

Обладнання: циліндр з в’язкою рідиною, секундомір, мікрометр, набір куль.

Теоретичні відомості

Всім реальним газам, рідинам та твердим тілам (далі – тілам) властива в’язкість або, інакше, внутрішнє тертя. В’язкість – це властивість газів, рідин та твердих тіл перешкоджати зсуву одної своєї частини (шару) відносно іншої (іншого шару) під дією зовнішніх сил.

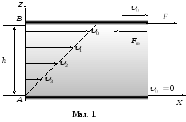На мал. 1 зображена в’язка течія шарів рідини. А та В – тверді пластини, між якими знаходиться шар рідини товщиною . Пластина А нерухома, а пластина В під дією зовнішньої сили та сили в’язкого тертя , що врівноважує зовнішню, рухається зі сталою швидкістю . Шар рідини, що знаходиться безпосередньо під пластиною В ніби прилипає до неї і рухається з тією ж швидкістю . Завдяки існуванню внутрішнього тертя до руху приєднуються і більш «глибинні» шари рідини, але швидкість їх руху , , …(мал. 1) зменшується з глибиною.

Головним законом в’язкої ламінарної течії рідини є формула Ньютона:

,

((1)

де – сила, дотична до площини S шару рідини, що зсувається відносно іншого, – коефіцієнт внутрішнього тертя (динамічної в’язкості) або просто динамічна в’язкість. Розмірність []Пас. Таким чином, сила внутрішнього тертя пропорційна градієнту швидкості руху рідини у площині, що перпендикулярна . При русі кулі у рідині (або у газі) теж виникає сила внутрішнього тертя, що перешкоджає її руху. Це обумовлено зменшенням відносної швидкості руху різних шарів рідини з віддаленням від поверхні кулі. Згідно із законом Стокса сила в’язкого тертя у цьому випадку:

,

((2)

де – радіус кулі, – швидкість її руху. Слід зазначити, що:

• пропорційна швидкості руху кулі;

• формула (2) виконується у тому випадку, коли характерний розмір тіла значно менший ніж лінійний розмір (у горизонтальній площині) посудини з рідиною;

• коефіцієнт 6 обумовлений сферичною формою тіла.

У випадку вертикального падіння кулі у рідині (мал. 2) на неї діють три сили: сила земного тяжіння , сила Архімеда та сила внутрішнього тертя . Спочатку (швидкість руху мала) і рух кулі – прискорений. Із зростанням швидкості зростає і сила внутрішнього тертя. З того моменту часу, коли досягне значення , швидкість кулі вже не буде змінюватись, тобто рух кулі буде рівномірним. Детально розглянемо цей випадок. Величина сили Архімеда: , a сила визначається співвідношенням (2); , – маса та об’єм кулі, – прискорення вільного падіння, – густина рідини. Запишемо другий закон Ньютона в проекції на вісь :

((3)

Користуючись цим рівнянням, можна визначити коефіцієнт внутрішнього тертя:

((4)

Оскільки

((5)

( – діаметр кулі, – густина кулі), то коефіцієнт в’язкості може бути розрахований за формулою:

(6)

Формула (6) для випадку, коли . Врахування скінченності призводить до формули:

(7)

Таким чином, вивчаючи рух кулі в області сталої швидкості, ми можемо за допомогою (7) розрахувати значення коефіцієнта в’язкості рідини.

Опис експериментальної установки

Для визначення коефіцієнта в’язкості рідини (гліцерину), що досліджується, використовують скляний циліндр (мал.2) з позначками () та (), відстань між якими дорівнює . Діаметр циліндра . Для проведення експерименту застосовують набір куль, діаметр яких визначають за допомогою штангенциркуля.

Проведення експерименту

1. Визначити температуру в лабораторії за допомогою термометра.

2. За допомогою штангенциркуля виміряти діаметр скляного циліндра .

3. За допомогою лінійки виміряти відстань між позначками i .

4. Таблиця № 1
   Т, К	, м	, м

   Дані пунктів 1-3 занести до таблиці № 1.
   
   
   
   
   
   

5. За допомогою мікрометра (або штангенциркуля) виміряти діаметр кульки .

6. Кинути кульку в спеціальний отвір у скляному циліндрі. У момент проходження кулькою позначки ввімкнути секундомір, а під час проходження позначки вимкнути його.

7. Пункт 4,5 виконати не менше 10 разів.

8. Результати вимірювань занести у таблицю № 2.

Обробка результатів

1. Результати вимірювань(пункти 5,6) заносяться у таблицю № 2.

2. Значення розраховуються за формулою (7); результати розрахунків занести в таблицю 2.

Таблиця № 2
Номер виміру i	Діаметр кулі ,м	Час падіння , c	i, Пас
Середнє значення
, Пас
, %

3. Для розрахунку середнього значення в’язкості використовують співвідношення:

4. Для розрахунку абсолютної похибки використовуються співвідношення (8): (8)

5. Користуючись таблицею № 3, оцінити масові долі гліцерину та води в рідині, що вивчається.

Таблиця № 3
Масова доля гліцерину, %	В’язкість , 10–3 Пас
	20 С		25 С	30 С
100	1495,0		942,0	622,0
99	1194,0		772,0	509,0
98	971,0		627,0	423,0
97	802,0		521,5	353,0
96	659,0		434,0	295,8
95	543,5		365,9	248,0

• Довірчий інтервал визначеного коефіцієнта в’язкості за довірчою ймовірністю¹;

• абсолютну похибку визначити за формулою (8).

Довідкова інформація

Фізичний параметр	Позначення
Прискорення вільного падіння у поверхні Землі	=
Густина гліцерину	=
Густина сталі (кульок)	=

Контрольні питання

1. Що називається в’язкістю? Який фізичний зміст коефіцієнта в’язкості? Яка його розмірність?

2. У чому полягає суть метода Стокса?

3. Чому виникає опір падінню куліі у рідині?

4. Чому, починаючи з деякого моменту часу, швидкість кулі не змінюється?

5. Як залежить стала швидкість куліі від її діаметра?

6. Чи залежить сила внутрішнього тертя від температури рідини? Чому?

Література

1. Грабовський Р.К. Курс фізики. – М.: Наука, 1974, С. 146, 167, 176.

2. А.В. Кортнев, Ю.В. Рублёв, А.Н. Куценко. Практикум по общему курсу физики М.: Высшая школа, 1993, с.154-156.

1 Значення довірчої ймовірності надається викладачем.

сторінка 4 з 4