
Рудницький В.Б._ Вища матем в правах и задачах
.pdf
Обчислити границi, використовуючи правило Лопiталя: |
|
|
|
|
|
|||||||||||||||||||||
|
|
tg x − x |
|
|
|
|
|
ln x |
|
|
|
√3 |
|
|
|
+ 1 |
||||||||||
|
lim |
|
|
|
lim |
|
|
lim |
1 + 2x |
|||||||||||||||||
1. |
|
|
2. |
|
|
|
; |
3. |
|
|
|
|
|
|
|
; |
||||||||||
x→0 x |
sin x; |
|
x→∞ |
√3 x |
x→−1 |
√2 + x + x |
||||||||||||||||||||
|
lim (1 |
− cos x) ctg x |
|
lim |
ex − 1 |
|
|
|
lim arcsin x |
|
ctg x |
|
||||||||||||||
4. |
; 5. |
sin 2x ; |
|
6. |
· |
; |
||||||||||||||||||||
x |
→ |
0 |
|
− |
|
x 0 |
|
x |
→ |
0 |
|
|
|
|
|
|
||||||||||
7. |
|
|
|
2 |
x; |
8. |
→ |
|
1 |
; |
9. |
|
|
|
|
|
1 |
|
|
|
|
|||||
lim (cos x)ctg |
lim (ln x) x |
lim (ex + x) x . |
|
|||||||||||||||||||||||
|
x→0 |
|
|
|
|
x→∞ |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
||||||
§5. Дослiдження поведiнки функцiї та побудова її графiка
Функцiя y=f(x) називається зростаючою (спадною) на деякому iнтервалi, якщо при x1<x2 виконується нерiвнiсть f(x1)<f(x2) (f(x1)>f(x2)).
Ознаки зростання та спадання функцiї.
1.Якщо f0(x) ≥ 0 на промiжку [a, b], то функцiя f(x) зростає на цьому промiжку.
2.Якщо f0(x) ≤ 0 на промiжку [a, b], то функцiя f(x) спадає на цьому промiжку.
Функцiя f(x) називається неспадною (незростаючою) на деякому iнтервалi, якщо для будь-яких x1 < x2 з цього iнтевалу f(x1) ≤ f(x2) (f(x1) ≥ f(x2)). Iнтервали, на яких функцiя не спадає або не зростає, називаються iнтервалами монотонностi функцiї. Точки, в яких перша похiдна функцiї не iснує або дорiвнює нулю називаються критичними.
Точка x0 називається точкою максимуму функцiї y = f(x), якщо для довiльного x iз околу точки x0 виконуюється умова f(x0) ≥ f(x). Точка x0 називається точкою мiнiмуму функцiї y = f(x), якщо для довiльного x iз околу точки x0 виконуюється умова f(x0) ≤ f(x). Точки мiнiмуму та максимуму називаються точками екстремума функцiї.
Необхiдна умова екстремуму. Якщо функцiя f(x) в точцi x0 має екстренум, то похiдна f0(x0) перетворюється в нуль або не iснує.
Достатнi умови екстремуму:
1. Якщо x0 – критична точка функцiї f(x) i для будь-якого достатньо малого h > 0 виконуються нерiвностi f0(x0 − h) > 0, f0(x0 + h) < 0, то функцiя f(x) в точцi x0 має максимум, якщо ж f0(x0 −h) < 0, f0(x0 +h) > 0, то функцiя f(x) в точцi x0 має мiнiмум. Якщо знаки f0(x0−h), f0(x0+h) однаковi, то функцiя f(x) в точцi x0 не має екстремуму.
2. Якщо f0(x0) = 0, f00(x0) 6= 0, то функцiя f(x) в околi точки x0 має екстренум, а саме, максимум, якщо f00(x0)<0, та мiнiмум, якщо f00(x0)<0.
61
Достатня умова опуклостi (вгнутостi) графiка функцiї.
Якщо f00(x)<0 на iнтервалi (a, b), то графiк функцiї опуклий на цьому iнтервалi; якщо ж f00(x)>0, то на iнтервалi (a, b) графiк функцiї вгнутий.
Якщо f00(x0) = 0 та для будь-якого досить малого h > 0 виконуються нерiвностi f00(x0−h) < 0, f00(x0+h) > 0 (або f00(x0−h) > 0, f00(x0+h) < 0), то точка x0 є точкою перегину. Якщо ж f00(x0 −h) i f00(x0 +h) однакового
знаку, то x0 не є точкою перегину.
Аудиторнi завдання
1.Знайти iнтервали монотонностi функцiй: а) y = x4 − 2x2 − 5; б) y = x/(x2 − 6x − 16).
2.Дослiдити на екстремум функцiї: а) y = x − ln(1 + x); б) y = x ln2 x.
3.Знайти точки перегину, iнтервали вгнутостi та опуклостi графiка функцiї y = ln(1 + x2).
4.Знайти найбiльше та найменше значення функцiї
y = 2x3 + 3x2 − 12x + 1 на вiдрiзку [−1; 5].
Домашнi завдання
1.Знайти iнтервали зростання та спадання функцiй: а) y = xe−x; б) y = (2 − x)(x + 1)2.
2.Знайти екстренуми функцiй:
а) y = x4 − 8x3 + 6x2 − 4x; б) y = (1 − x3)/x2.
3.Знайти точки перегину та iнтервали вгнутостi, опуклостi кривих: а) y = (x − 4)5 + 4x + 4; б) y = x4 − 8x3 + 24x2; в) y = xex.
4.Знайти найбiльше та найменше значення функцiй на заданих
вiдрiзках: |
|
|
|
|
б) y = x + 3√3 |
|
|
|
|
|
|
||||||
а) y = x4 − 2x2 + 3, [−3; 2]; |
|
|
, [−1; 1]. |
||||||||||||||
x |
|||||||||||||||||
|
|
|
|
|
|
Самостiйна робота |
|
|
|
|
|
|
|
||||
Знайти iнтервали монотонностi та екстремуми функцiй: |
|||||||||||||||||
1. y = 2x3 − 9x2 + 12x − 9; |
7. y = 2x − 3 |
√3 |
|
|
; |
|
|||||||||||
x2 |
|||||||||||||||||
2. y = x2(x − 2)2; |
|
8. y = √3 |
|
|
|
; |
|||||||||||
|
x2 + 4x + 3 |
||||||||||||||||
|
y = x |
(12 |
|
x2) |
|
|
y =pe |
|
|
||||||||
|
|
|
|
2x−x2 |
|||||||||||||
3. y = 2 |
− 3x2 |
− x3; |
9. y = 3 x(x |
− 2); |
|||||||||||||
4. |
|
|
|
− |
|
; |
10. |
|
|
|
; |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|||||||
5. y = (2x + 1)2 · (2x − 1)2; |
11. y = (x − 1)e4x+2; |
||||||||||||||||
62

6. y = (x3 − 9x2)/4 + 6x − 9; 12. y = x2 − 2 ln x.
Знайти точки перегину та iнтервали опуклостi та вгнутостi кривих:
1. y = ln(4 − x2); |
5. y = x4/(x3 − 1); |
||||||||
2. y = (x + 1)e2x; |
6. y = x3/(9 − x3); |
||||||||
3. y = x ln x2; |
|
7. y = xe1/x; |
|||||||
4. y = x3ex+1; |
|
8. y = (2x2 + 2 + 4x)/(2 − x). |
|||||||
Знайти найбiльше та найменше значення функцiї y = f(x) |
|||||||||
на вiдрiзку [a, b]: |
|
|
2. y = (x + 2)e1−x, [−2; 2]; |
||||||
1. y = ln(x2 − 2x + 2), [0; 3]; |
|||||||||
3. y = x3/(x2 − x + 1), [−1; 1]; |
4. y = √ |
|
|
|
|
, [−2; 2]; |
|||
x − x3 |
|||||||||
5. y = 4 − e−x2 , [0; 1]; |
6. y = (e2x + 1)/ex, [−1; 2]; |
||||||||
7. y = x ln x, [1/e2; 1]; |
8. y = 3x4 − 16x3 + 2, [−3; 1]; |
||||||||
x4 |
3 |
+ 7, [16; 20]; |
|
√ |
|
|
|
||
|
|
||||||||
9. y = 4 − 6x |
|
10. y = 2 x − x, [0; 4]; |
|||||||
11. y = 4 − x − 4/x2, [1; 4]; |
12. y = 2√ |
|
− x + 2, [1; 5]; |
||||||
x − 1 |
|||||||||
13.y = (10x + 10)/(x2 + 2x + 2), [−1; 2];
14.y = x2 + 4x + x16+ 2 − 9, [−1; 2];
2(x2 + 3)
15. y = −x2 + 2x + 5 , [−5; 1].
§6. Повне дослiдження функцiї та побудова її графiка
Схема повного дослiдження
1.Знайти область визначення функцiї y = f(x).
2.Дослiдити функцiю на парнiсть, непарнiсть та перiодичнiсть.
3.Знайти точки перетину графiка функцiї з осями координат.
4.Дослiдити функцiю на неперервнiсть; знайти точки розриву (якщо вони iснують) та встановити характер розриву, знайти асимптоти кривої y = f(x).
5.Знайти iнтервали зростання i спадання функцiї та її екстремуми.
6.Знайти iнтервали опуклостi та вгнутостi кривої i точки її перегину.
7.Побудувати графiк функцiї.
63

При знаходженнi асимптот користуємось такими означеннями:
а) пряма x = a є вертикальною асимптотою кривої y = f(x), якщо lim f(x) = +∞ або lim f(x) = −∞;
x→a |
x→a |
|
б) пряма y = b є горизонтальною асимптотою кривої y = f(x), |
||
якщо iснує границя |
lim f(x) = b або |
lim f(x) = b; |
|
x→+∞ |
x→−∞ |
в) пряма y = kx + b є похилою асимптотою кривої y = f(x), якщо iснують границi
k = x lim |
f(x) |
, b = x lim |
(f(x) − kx). |
||
x |
|||||
→±∞ |
|
|
→±∞ |
|
|
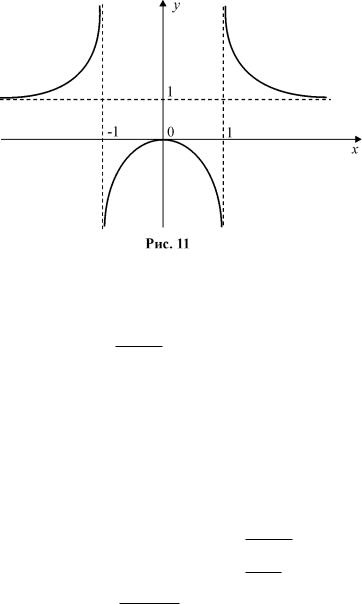
Приклад. Дослiдити функцiю y = |
x2 |
|
та побудувати її графiк. |
||
|
|
||||
|
|
|
x2 − 1 |
||
Розв’язання. 1. Область визначення x2 − 1 6= 0, x 6= ±1, отже,
x(−∞; −1) (−1; 1) (1; +∞).
2.Дослiджуємо функцiю на парнiсть, непарнiсть та перiодичнiсть:
f( x) = |
(−x)2 |
= |
|
x2 |
|
= f(x), |
|
(−x)2 − 1 |
x2 − 1 |
||||||
− |
|
|
|||||
тобто y = f(x) – парна функцiя. Дана функцiя не перiодична.
3. Знаходимо точки перетину графiка функцiї з осями координат.
|
x2 |
|
= 0; x = 0. Отже, графiк функцiї проходить через початок |
|||||||
|
x2 − 1 |
|||||||||
|
|
|
|
|
|
|
|
|
||
координат. |
|
|
|
|
|
|
|
|
||
4. В точках x1 = −1; x2 = 1 функцiя має розрив. Оскiльки |
||||||||||
|
|
|
|
x2 |
|
|
x2 |
|||
|
|
|
x→−1+0 x2 − 1 = −∞, |
x→−1−0 x2 − 1 = +∞, |
||||||
|
|
|
lim |
x2 |
|
lim |
x2 |
|
||
|
|
|
|
|
|
|||||
|
|
|
x→1+0 x2 − 1 = +∞, |
x→1−0 x2 − 1 = −∞, |
||||||
|
|
|
lim |
|
|
lim |
|
|
||
то в цих точках маємо розрив другого роду. Тому x1 = −1 i x2 = 1 є вертикальними асимптотами.
Знаходимо iншi асимптоти: |
|
|
|
|
|
|
|
|
|
k = lim |
f(x) |
= lim |
|
x2 |
|
|
= 0, |
||
x |
|
− |
1)x |
||||||
x→±∞ |
x→±∞ (x2 |
|
|
||||||
b = x lim (f(x) − kx) = x lim |
|
|
x2 |
|
= 1. |
||||
|
x2 |
− |
1 |
||||||
→±∞ |
|
→±∞ |
|
|
|
|
|||
64
Таким чином, y = 1 – горизонтальна асимптота.
5. Знаходимо iнтервали зростання та спадання функцiї та її екстремуми.
y0 = |
2x(x2 − 1) − x2 · 2x |
= |
2x3 − 2x − 2x3 |
= |
−2x |
|
(x2 − 1)2 |
(x2 − 1)2 |
(x2 − 1)2 |
||||
|
|
|
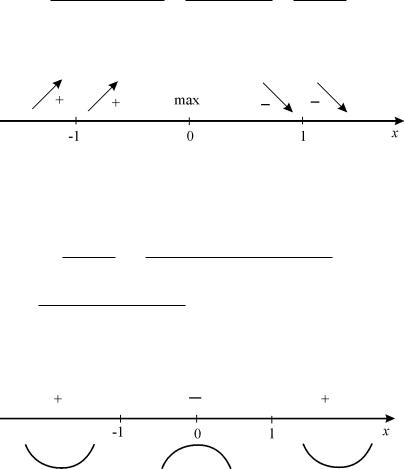
y0 = 0, якщо −2x = 0, x = 0. Таким чином, маємо три критичнi точки x1 = 0, x2 = −1, x3 = 1. Визначаємо знак похiдної на кожному промiжку.
В точцi x = 0 функцiя змiнює знак з "+" на "−", тому x = 0 є точкою максимуму i ymax = f(0) = 0.
6. Знаходимо iнтервали вгнутостi i опуклостi та точки перегину графiка функцiї
|
|
|
|
2x |
|
2 |
|
|
|
2 + 2x 2(x2 |
|
1) |
|
2x |
|||||
|
y00 |
= |
− |
= |
−2(x |
|
− 1) |
· |
|
|
− |
|
· |
|
= |
||||
|
(x2 − 1)2 |
|
|
|
|
|
(x2 − 1) |
4 |
|
|
|
|
|
||||||
|
= |
|
(x2 − 1)(−2x2 + 2 + 8x2) |
= |
|
6x2 + 2 |
= |
2(3x2 + 1) |
. |
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
(x2 − 1)4 |
|
|
|
(x2 − 1)3 |
|
|
(x2 − 1)3 |
||||||||
Оскiльки 3x2 + 1 6= 0, то критичними точками другого роду будуть |
|||||||||||||||||||
x1 = −1 |
i |
x2 = 1. Визначаємо |
знак другої |
похiдної |
на отриманих |
||||||||||||||
вiдрiзках: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так як при переходi через точки x1 = −1 i x2 = 1 друга похiдна змiнює знак на протилежний, то цi точки є точками перегину.
7. Будуємо графiк функцiї. Спочатку штрихованими лiнiями наносимо асимптоти, потiм точки екстремуму та перегину i сам графiк (рис.11).
65
|
|
|
|
|
|
|
|
|
|
Аудиторнi завдання |
|
|
|
|
|
|
|
|
||||||||||||||||
Дослiдити функцiю та побудувати її графiк: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1. y = |
|
x3 |
|
; |
|
|
2. y = |
|
|
2x − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
|
(x − 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Домашнi завдання |
|
|
|
|
|
|
|
|
||||||||||||||||
Дослiдити функцiю та побудувати її графiк: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1. y = |
|
4x |
; |
|
|
2. y = |
|
|
x3 |
|
|
|
|
; |
|
3. y = x2e−x. |
|
|
|
|
||||||||||||||
4 + x2 |
|
|
2(x + 1)2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Самостiйна робота |
|
|
|
|
|
|
|
|
||||||||||||||||
Дослiдити функцiю та побудувати її графiк: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1. y = |
x2 + 1 |
; |
|
2. y = |
|
|
|
x3 |
|
|
; |
|
|
|
|
|
3. y = |
8(x − 1) |
; |
|
|
|
||||||||||||
|
|
|
|
|
+21 |
|
|
|
|
|
(x + 1)2 |
|
|
|
||||||||||||||||||||
|
|
|
x |
2 |
− 1 |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|||||||||
4. y = |
|
12x |
|
; |
|
5. y = |
|
|
|
|
x |
|
|
|
|
|
; |
|
|
6. y = |
|
− 4 |
; |
|
|
|
|
|||||||
9 + x2 |
(x |
|
|
1)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y = |
|
|
|
|
|
|
y = |
|
− x + 1 |
|
|
y = x + ln(x2 |
|
4) |
|
||||||||||||||||||
7. |
x2 + 2x; |
8. |
|
|
|
; |
9. |
− |
; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
− |
1 |
|
|
|
|
|
ln x |
|
|
|||||||||||||||||
10. y = xex; |
|
|
11. y = xe1/x; |
|
|
|
12. y = |
|
|
. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
66
§7. Функцiї кiлькох змiнних
Бiльшiсть процесiв, якi вiдбуваються в навколишньому свiтi, характеризуються багатофакторними залежностями. Дослiдження таких залежностей вимагає введення поняття функцiй кiлькох змiнних. Аналогiчно, як з функцiєю однiєї змiнної y = f(x) можна розглянути залежнiсть вiд кiлькох незалежних змiнних (x1, x2, . . . , xn). Цю залежнiсть записуємо так:
z = f(x1, x2, . . . , xn). |
(1) |
При цьому числа x1, x2, . . . , xn називають незалежними змiнними, z
– функцiєю. Iнколи набiр iз n дiйсних чисел x1, x2, . . . , xn називають точкою n-вимiрного простору, а числа x1, x2, . . . , xn називаються координатами точки. Сукупнiсть значень (x1, x2, . . . , xn) для яких функцiя
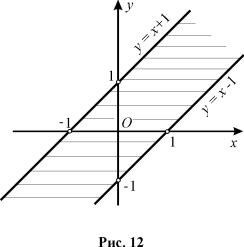
(1) має змiст, називається областю визначення функцiї, а значення, якi приймає функцiя z – називають областю значень функцiї i позначають через G. Причому на вiдмiну вiд функцiї однiєї змiнної, область визначення функцiї (1) складається з n-вимiрної множини. Наприклад, область визначення функцiї z = arcsin(x − y) є смуга координати якої задовольняють подвiйну нерiвнiсть −1 ≤ x − y ≤ 1. Ця смуга обмежена двома паралельними прямими y = x + 1 i y = x − 1 (рис. 12).
67

Якщо вiдстань мiж двома точками (x1, x2, . . . , xn) i (y1, y2, . . . , yn) визначається за формулою
d = v |
n |
(xk |
− |
yk)2 |
, |
(2) |
uk=1 |
|
|
|
|
||
uX |
|
|
|
|
|
|
t
то такий простiр називається n-вимiрним евклiдовим простором i позначається Rn. Як частковий випадок n-вимiрного простору розглядають двовимiрний R2 i тривимiрний R3, тодi точка у двовимiрному просторi позначається M(x, y) або (x, y), а точка тривимiрного простору позначається M(x, y, z) або (x, y, z).
Отже, функцiя n-змiнних залежить вiд n-незалежних змiнних (1), геометрична iнтерпритацiя даної функцiї неможлива, але у випадку двох змiнних, як ми знаємо, функцiя f(x, y) = 0 iнтерпритується у декартовiй системi координат як крива, a у випадку трьох змiнних f(x, y, z) = 0 – як поверхня. Для зручностi функцiю n-змiнних z = f(x1, x2, . . . , xn) при n > 3 досить часто розглядають як функцiю точки P (x1, x2, . . . , xn) i пишуть z = f(P ).
Для функцiй кiлькох змiнних справедливi батаго понять i тверджень як i для функцiї однiєї змiнної. Так, розглядаючи функцiю трьох змiнних, зафiксуємо деяке значення y = y0, тодi одержимо функцiю однiєї змiнної x з параметром y0. Якщо поверхню z = f(x, y) перетнути площиною z = const, то також одержимо функцiю f(x, y) = const, яка називається лiнiєю рiвня (iзолiнiєю). Якщо цi лiнiї спроектувати на площину xOy, то отримаємо сiм’ю лiнiй, якi називають горизонталями. Наприклад,
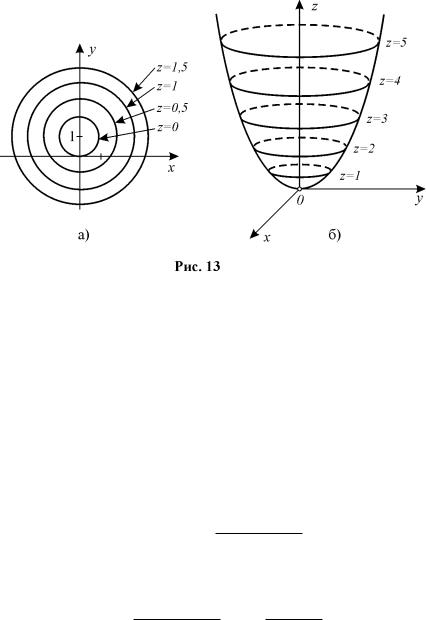
для параболоїда обертання z = x2 + y2 (рис. 13 a)) лiнiями рiвня є
√
кола радiуса c. Поняття лiнiї рiвня використовується при складаннi географiчних карт, де вони показують лiнiї однакової висоти над рiвнем моря, в економiцi вони показують вартостi основного капiталу та затрат працi, якi забезпечують одну i ту ж вартiсть виробленої продукцiї.
Приклад 1. Побудувати лiнiї рiвня функцiї z = x2 + y2 − 2y. Розв’язання. Лiнiя рiвня z = c – це крива на площинi xOy, яка задана
рiвнянням x2 + y2 − 2y = c або x2 + (y − 1)2 = c + 1. Це рiвняння кола з
p
центром в точцi (0; 1) i радiусом |c + 1| (рис. 13 a),б)).
68
Бiльшiсть понять, як було сказано вище, для функцiї однiєї змiнної може бути перенесена на випадок функцiї кiлькох змiнних.
Число a називається границею функцiї z = f(x, y) при x→x0, y→y0, якщо для будь-якого, як завгодно малого ε > 0, знайдеться таке додатне число δ > 0 (δ = δ(ε)) таке, що для всiх точок (x, y) вiдстань вiд яких до точки (x0, y0) менша δ, виконується нерiвнiсть
|
|
|
|
|
|f(x, y) − a| < ε. |
|
|
|
|
|
|
|
|
|
|||||||||||
Цей факт позначається так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
lim |
f(x, y) = a. |
|
|
|
|
|
|
|
|
(3) |
||||||||||
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y→y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приклад 2. Знайти границю lim |
ln(1 − x2 − y2) |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y→ρ =p x2 |
+ y2 |
|
|
|
x 0 y 0 |
|||||||||||
|
|
|
|
|
|
|
|
|
x→0 |
|
x2 |
+ y2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. Позначимо через |
|
|
|
|
|
|
|
|
|
|
|
|
. Умова → , → |
||||||||||||
рiвносильна тому, що |
ρ |
→ |
0 |
. Запишемо |
границю у виглядi |
|
|||||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||||
I = lim |
ln(1 − x2 − y2) |
= lim |
|
ln(1 − ρ2) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y→→0 |
|
px |
2 |
+ y |
2 |
|
|
|
ρ |
→ |
0 |
|
|
ρ |
|
||||||||||
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
69
Маємо невизначенiсть типу 00 при ρ → 0, отже, можна застосувати правило Лопiталя
|
(ln(1 − ρ2))0 |
|
|
1 |
(−2ρ) |
|
0 |
|
||||
I = lim |
= lim |
1−ρ2 |
= |
= 0. |
||||||||
|
|
|
||||||||||
(ρ2)0 |
|
1 |
||||||||||
ρ 0 |
ρ |
→ |
0 |
1 |
|
|
||||||
→ |
|
|
|
|
|
|
|
|
|
|
||
Функцiя z = f(x, y) називається неперервною у точцi (x0, y0), якщо
lim f(x, y) = f(x0, y0). |
(4) |
Тi точки, в яких умова (4) не виконується, називаються точками розриву, якi утворюють лiнiї розриву.
Приклад 3. Знайти точки розриву функцiй: |
||||||||
1 |
|
б) z = |
1 |
|
|
|
||
а) z = |
|
; |
|
. |
|
|
||
x2 + y2 |
2x + y + 1 |
|||||||
Розв’язання. а) Функцiя z= |
1 |
|
має єдину точку розриву в почат- |
|||||
x2 + y2 |
|
|||||||
ку координат O(0, 0), в якiй вона не визначена. При необмеженому |
||||||||
|
|
|
наближенi точки P (x, y) до точки |
|||||
|
|
|
|
|
1 |
|
||
|
|
|
O(0, 0) функцiя z= |
|
прямує |
|||
|
|
|
x2 + y2 |
|||||
до нескiнченностi.
1
б) Функцiя z= 2x + y + 1 визначе-
на i неперервна в усiх точках, крiм точок, якi задовольняють рiвняння 2x + y + 1 = 0. Це рiвняння прямої, кожна точка якої є точкою розриву. Таким чином, точки розриву утворюють цiлу пряму – лiнiю розриву для даної функцiї.
Величина |
|
z = f(x, +Δx, y + y) − f(x, y) |
(5) |
називається повним приростом функцiї z = f(x, y). Якщо розглядається тiльки прирiст аргументу x або y, то одержанi прирости
xz = f(x + x, y) − f(x, y), |
yz = f(x, y + y) − f(x, y) |
називаються частинними приростами, причому |
|
z 6= |
xz + yz. |
70
