Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Херсонский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Рудницький В.Б._ Вища матем в правах и задачах

.pdf

Скачиваний:

Добавлен:

07.02.2016

Размер:

703.72 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Таким чином, в точцi x1 = 0 функцiя f(x) має розрив першого роду типу "стрибок". Визначимо величину h cтрибка: h = f(x0 +0)−f(x0 −0). Маємо h = f(0 + 0) − f(0 − 0) = 1 − 0 = 1.

В точцi x2 = 2

lim f(x) =

lim

−

1)2 = 1;

lim f(x) =

lim (5

−

x) = 3.

→

−

→

−

→

2+0

→

2+0

x 2

Тому в точцi x2 = 2 функцiя f(x) також має розрив першого роду типу "стрибок". Величина стрибка h = f(2 + 0) − f(2 − 0) = 2.

Будуємо графiк (рис. 10)

Приклад 4. Дослiдити функцiю f(x) = 8 x−3 + 1 на неперервнiсть в точках x1 = 3, x2 = 4.

Розв’язання. В точцi x1 = 3

+ 1 = 8 ∞ + 1 = ∞.

x→3−0

−

+ 1 = 8−∞ + 1 = 1;

x→3+0

−

lim

Отже, в точцi x1 = 3 функцiя має розрив другого роду.

В точцi x2 = 4

x=4

x→4−0

−

= 9;

x→4+0

−

lim

+1 = 9;

f(4) =

= 9,

тобто, в точцi x2 = 4 функцiя неперервна.

Аудиторнi завдання

Обчислити границi:

x2+1

xlim

;

xlim

3. xlim ln

1−4x

;

2 !

;

x + 8

x2+1

2 4x

x+3

→∞

−

→∞

−

3x+4

x+2

−1

xlim

3x+2

; 5.

lim (3x

−

2) x

→∞

→

6. Дослiдити функцiю на неперервнiсть та побудувати її графiк,

x + 4, x < −1,

якщо f(x) = 1/x, −1 ≤ x < 1,

x, x ≥ 1.

7.Дослiдити функцiю f(x) = 21/(x−2) + 4 на неперервнiсть в точках x1 = 2, x2 = 3.

Домашнi завдання

Обчислити границi:

;

2. x→2

−

1. x→∞

2x + 1

3x−4

lim

2x − 3

lim (2x

3)x2/(x

3. xlim ln

x + 2

;

4. xlim

−

4x + 2

! ;

x + 1

x+3

2x + 1

→∞

−

5. x→∞

ln(3x

;

6. x→0

−

lim (2x + 1)(ln(3x + 1)

2))

lim (cos x) sin x

7. Дослiдити функцiю на неперервнiсть та побудувати схематично її

x <

1 x,

x ≤

π/2.

графiк, якщо f(x) = cos x,

≥

x < π/2,

−

8. Дослiдити

функцiю на неперервнiсть в даних точках:

а) f(x) = 31/(x+1), x1 = 1, x2 = −1;

f(x) =

3x − 2

= 0

б)

x + 2 ,

−

Самостiйна робота

Обчислити границi:

x + 4

−3x

1. x→∞ x + 8

3x+2;

lim

3. x→∞ x + 4 3x+4;

lim

x − 1

x+1;

x→∞

lim

x + 5

x→∞

3x + 5

;

lim

3x + 4

x→∞

1 + 2x

−x

3 + 2x

;

lim

x−2

11.

4 + 3x

x→∞

1 +23x

;

lim ln

13.

lim (5

−

2x)x /(x−2)

;

→

15.

lim (3x − 8)(x+1)/(x−3);

x→3

6−cos x

ctg2 x

17.

x→0

;

lim

x→∞

−4x

1 + 2x

;

lim

2x − 1

3x−1

lim

;

2x + 4

x→∞

3x + 4

−2x

x+1;

lim

8. x→∞

1 − 2x

2x;+3

lim

− 2x

10.

x + 3

;

x→∞

lim ln

x + 2

12.

x − 4

;

x→∞

lim ln

x + 3

14.

lim (7 − 6x)x/(3x−3);

x→1

lim

sin2 x

16.

3−cos x

;

→

18.

lim (3

2 cos x)−

−

sin2 x

→

Дослiдити функцiї на неперервнiсть та побудувати схематично їх графiки:

f(x)= (x+1)2, 0 < x 2

f(x)=

2x, 1 < x

x + 1, x ≤ 0

x2 + 1, x ≤

−x + 4, x > 2 ≤

x + 2, x >≤3

√

sin x, x < 0

x, x ≤ 0

f(x)=

0, 0−< x ≤ 2

f(x)=

x, 0 ≤ x ≤ 2

x 2, x > 2

0, x > 2

−

1, x < 0

1, x 0

f(x)= sin x, 0

x < π

f(x)=

2x, 0 < x

−

≤

3, x π≤

x + 3, x >≤2

x +≥2, x

1, x < 0

f(x)= x3, −2 < x ≤ 1

f(x)= cos x, 0 ≤ x ≤ π

−

≤ −

−

2, x > 1

1 − x, x > π

2, x < −1

tg x + 1, x ≤ π/4

f(x)=

1 − x, −1 ≤ x ≤ 1

10.

f(x)=

x+1, π/4 < x < 5

ln x, x > 1

6, x

≥

Дослiдити функцiї на неперервнiсть в заданих точках:

1.	f(x) = 41/(3−x) + 2;					x1 = 2,		x2 = 3.
2.	f(x) = 21/(x−5) + 1;					x1 = 4,		x2 = 5.
3.	f(x) = 91/(2−x);					x1 = 0,		x2 = 2.
4.	f(x) = 54/(3−x) + 1;					x1 = 2,		x2 = 3.
5.	f(x) = 42/(x−1) − 3;					x1 = 1,		x2 = 2.
6.	f(x) = 3x/(x − 4);					x1 = 4,		x2 = 5.
7.	f(x) = (x + 5)/(x − 2);					x1 = 3,		x2 = 2.
8.	f(x) =			1	;	x1	= 1,	x2	= 5.
		(x − 1)(x − 5)
9.	f(x) =			x	;	x1	= 2,	x2	= −4.
		(x	−	2)(x + 4)
10.	f(x) = 4x/(x + 5);					x1	= −5,	x2	= −4.

§3. Похiдна функцiї

Нехай на деякому iнтервалi (a, b) задано функцiю y = f(x). Вiзьмемо деяку точку x (a, b) i надамо x довiльного приросту x такого, щоб точка x + x також належала iнтервалу (a, b). Знайдемо прирiст функцiї

y = f(x + x) − f(x).

Похiдною функцiї y = f(x) в точцi x називається границя вiдношення приросту функцiї y в цiй точцi до приросту аргументу x, коли прирiст аргументу прямує до нуля.

Похiдна функцiї y = f(x) в точцi x позначається одним iз таких

символiв:

y0;

;

; f0

(x).

Таким чином, за означенням

f0(x) = lim

= lim

f(x +

x) − f(x)

x→0

Операцiя знаходження похiдної вiд функцiї називається диференцiюванням. Теорема. Якщо функцiї u=u(x), v=v(x) диференцiйовнi в точцi x, то диференцiйовними будуть сума, рiзниця, добуток i частка цих функцiй (частка за умови, що v(x) 6= 0) i при цьому справедливi такi правила диференцiювання:

C0=0, (Cu)0=Cu0, (u

v)0

=u0

, (uv)0=u0v+uv0,

0 =

u0v − uv0

Тут C – стала.

Якщо y=f(u), u=ϕ(x), тобто y=f(ϕ(x)) – складена функцiя i icнують похiднi yu0 та u0x, то функцiя y = f(ϕ(x)) теж має похiдну, яку можна

обчислити за формулою:

yx0 = yu0 u0x.

Таблиця похiдних

1.(uα)0 = αuα−1 · u0 (α R);

2.(au)0 = au · ln a · u0;


			1
4.	(loga u)0		=						· u0;
					u ln a
6.	(sin u)0	= cos u				·		u0		;
	(tg u)0	=	1
8.							· u0;
				cos2 u


3.	(eu)0 = eu · u0;
		1
5.	(ln u)0 =				· u0;
			u					u0
7.	(cos u)0	=		−		sin u	·		;
						1
9.	(ctg u)0	= −						· u0;
						sin2 u

10.

(arcsin u)0 =

√

· u0;

11.

(arccos u)0

= −

√

· u0;

1 − u2

12.

(arctg u)0

· u0;

13.

(arcctg u)0

= −

· u0;

1 + u2

14.

(sh u)0 = ch u · u0;

15.

(ch u)0

= sh u · u0;

16. (thu)0 =

· u0;

17. (cth u)0 = −

· u0.

ch2 u

sh2 u

Приклад 1. Знайти похiднi функцiй:

x4 + 1

а) y = 4arcsin x;

б) y = (3x − 2) · sin3 2x;

в)

−

Розв’язання.

а) y0=(4arcsin x)0=4arcsin x· ln 4 · (arcsin x)0=4arcsin x · ln 4 ·

√

;

1 − x

б)

y0 = (3x

−

2)0

sin3

2x + (3x

3−

(sin3 2x)0 = 3 sin3 2x+

2x · cos 2x;

+(3x − 2) · 3 sin

2x · cos 2x ·

2 = 3 sin 2x + 6(3x − 2) sin

в) y0 =

(x4 + 1)0 · (x4 − 1) − (x4 + 1) · (x4 − 1)0

3 4

+ 1)

(x4

3− 1)2

4x (x − 1)

− (x

· 4x

· (−2)

−8x

(x4 − 1)2

Логарифмiчне диференцiювання

Логарифмiчною похiдною функцiї y = f(x) називається похiдна вiд логарифма цiєї функцiї, тобто

(ln f(x))0 = f0(x) . f(x)

Послiдовне застосування логарифмування та диференцiювання функцiї називається логарифмiчним диференцiюванням.

Приклад 2. Знайти похiдну функцiї y = (cos 2x)x3 . Розв’язання. Логарифмуємо дану функцiю:

		ln y = ln(cos 2x)x3		= x3 · ln(cos 2x).
Диференцiюємо обидвi частини по x:
		(ln y)0	= (x3)0 · ln(cos 2x) + x3(ln(cos 2x))0.
Звiдки				1
	y0
		= 3x2	· ln(cos 2x) + x3 ·			· (− sin 2x)	· 2
	y				cos 2x

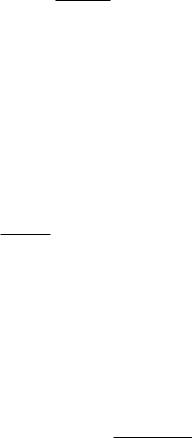
y0 = y · 3x2 ln(cos 2x) − 2x3 sin 2x cos 2x

y0 = (cos 2x)x3 · (3x2 ln(cos 2x) − 2x3 · tg 2x).

Якщо залежнiсть мiж змiнними x та y задана у неявному виглядi рiвнянням F (x, y)=0, то для знаходження похiдної y0=yx0 в простiших випадках достатньо продиференцiювати обидвi частини рiвняння F (x, y)=0, вважаючи y функцiєю вiд x. З отриманого рiвняння, лiнiйного вiдносно y0, знайти похiдну.

Приклад 3. Знайти похiдну функцiї y0, якщо x3 + y3 − 3xy = 0. Розв’язання. Диференцiюємо обидвi частини рiвняння, вважаючи y

функцiєю вiд x:

Звiдки знаходимо

3x2 + 3y2 · y0 − 3y − 3xy = 0.

3y − 3x2

y0 =

3y2 − 3x

Аудиторнi завдання

Знайти похiднi функцiй:

√4

1. 2√x −2

x +

2. y = (x

−3x+3)(x +2x−1);

3. y = x + x − 1 ;

4. y = (5x3 + x2

−

4)5;

x3 + 1

5. y =

;

6. y =

3 tg

− tg x + x;

√

2x − 1

+ 2)

y = sin2(cos 3x)

y = arctg2

;

x + 3

9. y = 102x−3;2

10. y = 3rln

sin

;

+3x−2);

11. y = sin(ex

12. y = xln x;

13. y = (x2 + 1)sin x;

14. x4 + y4 = x2y2.

Домашнi завдання

Знайти похiднi функцiй:

√7

√3

1. y = 5x

− 3

x +

+ 4;

2. y = 3x

+ 5

−

;

3. y = x3 · sin x;

4. y = (x9 + 1) cos 5x;

5. y =

sin2 x

;

6. y =

3x + 1

;

x3 + 1

arcsin(1

−

8. y =

7. y = (x5 +43x − 1)4;

x4 + sin4 x;

earctg √x

9. y = 2−

cos

;

10.

;

y =p

11.

y = sin(tg √

);

12.

y = ln5(x − 2−x);

13.

y = (2sin 3x + cos 3x)3

;

14.

y = x3 cos 2x

e−x

;

y = (sin 3x)

cos 5x

;

y = (x

+ 1)

tg·

;

15.

16.

17.

y = (tg 3x)x4 ;

18.

y = (ctg 5x)x3−1;

19.

− x

− y

= 3;

20.

= 5.

xy − arctg y

Самостiйна робота

Знайти похiднi функцiй:

√5

√

1. y = 2x

−

+ x

+ 3 x;

2. y = x

+ x

− 4x +

2 ; x4

cos 8x5

−

3. y = 3 3x4

+ 2x

− 5 +

;

2)5

5. y = sin

2x ·

;

7. y = x2 · 41−x

+ π;

9. y = x3esin(1−2x);

11.

y =

arctg2 5x

ln(x

−

;

cos x

·2

13.

y = 3

ln(x

− 3x + 7);

15.

y =

(x − 4)2

;

earcctg x

17.

y =

ln(5x − 3)

;

4 tg 3x4

19.

y =

9 arctg(x + 7)

;

(x − 1)2

21.

2x + 3

;

y = 3

2x −

lg(4x + 7)

23.

y = sin3(e5x − 3);

25.

y = ln cos(1 − e

√

);

27.

y = ln arccos(3 + 7√

);

29.

y = sin5

√5x −3 x2

;

31.

√

+ 1));

y = arctg(ln(e

33.

y = sin4(1 − 2√

−1);

2x3

−

3x + 1 ;

4. y = 3 (x − 3)4 −

6. y = cos

3x · tg(4x3 + 1)

;

8. y = (1 − 4x) · e−x + ln 2;

10.

y = 5cos 4x · (1 + 4x3);

12.

y = log4(x − 1) · arcsin

2 x;

14.

y = log2(x −34) · arcctg

7x;

16.

y =

√

e−x

;

x3 + 5x − 1

18.

y =

sin (5x + 1)

;

lg(3x − 2)

20.

y =

7 arccos(4x − 1)

;

(x + 2)4

22.

x + 1

;

y =

x − 1

arcctg(7x + 2)

24.y = ln 3x − x +2 1 ;


26.	y = arcsin7(1 −5x	8x);
28.	y = (4 − 7x) e	+ sin 3;
30.	y = 4x7 · 35+2x − √					;
					3
32.	y = cos tg(x − √3			);
			x4
34.	y = (1 − x)4 · 9arcsin √							;
							x

35.	y = arccos ln(e−3x + 4x);
37.	y = (arcsin 7x)√										;
										3x
					2			cos 3x
39.	y = (1 − 8x						)		2		;
41.	y = (tg 7x)4−x ;
43.	y = (ctg(5 + 3x))−x;
45.	y = (x + 3)ln(1+e−x);
47.	y = (arccos(x + 2))tg 3x;
49.	y = (lg(8x + 3))tg 5x;
51.	y = (ln(x + 3))sin √												;
												x
53.	xy2			−	arctg(x				−	y) = 5				;
	x	5				4
55.			sin 7y + y						= 3;

36.

y = ln arcsin(1 + √3

);

38.

y = (3x − cos x)x2 ;

40.

y = (3 − 2x)√

;

42.

y = xsin 3x;

44.

y = (arctg(33− 2√

))x;

46.

y = (tg 3x)x ;

48.

y = (cos(2x − 5))arctg 5x;

50.

√

arccos 3x

;

y = ( x + 5)

√

52.y + 1 ) = 4;· x − sin(x − y

54.	y tg(xy) − ex = 2;
56.	cos(3x + 2y) + √	x	= 0.

§4. Похiднi вищих порядкiв. Правило Лопiталя

Похiдною другого порядку функцiї y = f(x) називається похiдна вiд її

першої похiдної, тобто

y00 = (y0)0.

Похiдною n-го порядку функцiї y = f(x) називається похiдна вiд похiдної (n − 1)-го порядку даної функцiї, тобто

y(n) = (y(n−1))0.

Приклад 1. Знайти похiдну третього порядку функцiї

y = (1 + 4x2) arctg 2x.

Розв’язання. Послiдовно знаходимо y0, y00, y000.

y0 = (1 + 4x2)0

· arctg 2x + (1 + 4x2)(arctg 2x)0 =

= 8x arctg 2x + (1 + 4x2) ·

· 2 = 8x arctg 2x + 2;

1 + 4x2

y00 = (y0)0 = (8x arctg 2x + 2)0

= 8 arctg 2x + 8x

2 =

1 + 4x2

= 8 arctg 2x +

16x

;

1 + 4x2

= 8 arctg 2x +

16x

8 2

(1 + 4x2) 16x

y000

−

1 + 4x2

(1 + 4x2)2

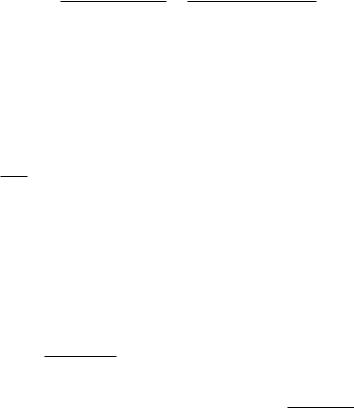
=	16	+	16 + 64x2 − 128x2	=	16 + 64x2 + 16 − 64x2	=	32	.
	1 + 4x2		(1 + 4x2)2		(1 + 4x2)2		(1 + 4x2)2

Для розкриття невизначеностей 00 , ∞∞ та iн. при обчисленнi границь

використовують правило Лопiталя.
Теорема. Нехай функцiї f(x)			i ϕ(x) визначенi i диференцiйовнi в
околi точки x0, за винятком, можливо, самої точки x0, причому
lim f(x) =	lim ϕ(x) = 0,		lim f(x) =			lim ϕ(x) =		,
x x0	x	або x		→	x0	x	→∞	∞
→	→∞			→			→∞

i у вказаному околi ϕ0(x) 6= 0. Тодi iснує i границя вiдношення функцiй

lim f(x) , i цi границi рiвнi мiж собою:

x→x0 ϕ(x)

lim	f(x)	=	lim	f0(x)	.
	ϕ(x)
x→x0			x→x0	ϕ0(x)

Якщо вiдношення похiдних знову веде до невизначеностi типу 00 та ∞∞, то правило Лопiталя застосовують до цього вiдношення.

Невизначеностi типу ∞ − ∞, 0 · ∞, 1∞, ∞0, 00 спочатку необхiдно звести до невизначеностi 00 та ∞∞.

Приклад 2. Обчислити границi, використовуючи правило Лопiталя:

а) x

lim

π − 2 arctg x

;

б)

lim tg 2x

ln tg x

;

lim (tg x)tg 2x

ln(1 + 1/x)

→

∞

→

в) x

→

Розв’язання. а) маємо невизначеннiсть типу

π−2 arctg x

(при

→

∞

arctg x

→

π/2

;

1/x

→

). Тодi x

lim

ln(1+1/x)

→ ∞

−2 ·

2 ·

x2+x

lim

1 + x2

lim

1 + x2

= 2

lim

= 2;

1 +11/x · −x2

1 + x

· x2

→

∞

→

∞

→

∞ 1+x

б) маємо невизначеннiсть типу ∞ · 0

lim tg 2x

ln tg x = lim

ln tg x

lim

ctg 2x

= x

→

lim

sin2

lim

sin2

cos2 x

− x

→

π 2 tg x

= − x

→

π 2 sin x cos x

1		·	1
tg x		·	cos2 x	=
−			2	=
			2
	sin2 2x

= − lim sin 2x = −1;

x→π4

в) маємо невизначеннiсть типу 1∞

lim (tg x)tg 2x		= lim eln(tg x)tg 2x = lim etg 2x ln(tg 2x).
π				π	π
x→ 4				x→ 4	x→ 4
lim tg 2x			·	ln(tg x)	. Ця границя дорiвнює −	1	(див. прикл.
Тепер знайдемо x	π		·		. Ця границя дорiвнює −		(див. прикл.
→	4
б). Отже,				lim (tg x)tg 2x = e−1.
				lim (tg x)tg 2x = e−1.
				π
				x→ 4
		Аудиторнi завдання
1. Знайти похiдну другого порядку функцiї:
а) y = (x2 + 1) · ln(1 + x2);					б) y = e−3x · (cos 2x + sin 2x).

2.Знайти похiдну n-го порядку функцiї f(x) = x +1 2 .

3.Обчислити границi:

а)

lim

x cos x − sin x

;

б)

lim

e7x − 1

;

x→0

;

x→0

tg 3x

в)

г)

x→0

sin x

x→∞ x · sin x

lim

Домашнi завдання

1. Знайти похiднi третього порядку для функцiй:

а) y = ex sin 2x;

б) y = x cos 2x;

в) y = x4 ln x;

г) y = x arccos x;

д) y = (7x − 4)6; ж) y = x + arctg x.

2.Знайти похiдну n-го порядку функцiї y = ln x.

3.Обчислити границi:

πx

а) x→0

;

б) x→1

−

; в)

x→2

;

x sin 7x

−

ln x

lim 1 − cos 7x

lim

ctg

−

lim

г) x→0

;

д) x→∞ x + 1

;

ж) x→∞ x2 + 1 .

lim (x2e1/x )

lim

Самостiйна робота

Знайти похiднi третього порядку функцiй:

1. y = e

cos x;

2. y = (2x + 1)

;

3. y =

ln(x2

−

;

4. y = arcsin x;

5. y = sin(x3 + π);

6. y = 2x ;

7. y = 21 x2ex;

8. y = ln3 x;

9. y = (x + 1) ln(x + 1).

Знайти похiднi n-го порядку функцiй:

3. y = √

1. y = 2x;

2. y = xe3x;

x + 7

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.07.2025270.85 Кб0Розділ_9_10.doc
#
01.05.2025216.58 Кб0розмноження.doc
#
10.09.2019153.6 Кб2РОЗРОБКА СТРАТЕГІЇ МАРКЕТИНГУ.doc
#
01.05.20251.22 Mб0РОЛЬ СТВОЛА МОЗГА И МОЗЖЕЧКА В РЕГУЛЯЦИИ ПОЗЫ И...doc
#
01.04.2025122.07 Mб0РТС. Конспект лекцій.doc
#
07.02.2016703.72 Кб82Рудницький В.Б._ Вища матем в правах и задачах.pdf
#
23.08.2019260.1 Кб2Рук1.doc
#
17.08.2019101.15 Кб10с пылью и сором.docx
#
01.05.2025580.1 Кб0С.. Zapiska_DP1 (2).doc
#
04.11.2018272.38 Кб4Сам раб БМ 1.doc
#
13.11.2018584.7 Кб9Сам робота ділова нова.doc