
Рудницький В.Б._ Вища матем в правах и задачах
.pdf
3. |
Перевiрити, чи перетинаються прямi |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x + 2 |
= |
y − 3 |
|
= |
z − 4 |
|
та |
|
x |
= |
|
y + 4 |
= |
z − 3 |
. |
|
|
|
|
||||||||||||||||||||
|
|
−1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
3 |
|
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||
4. |
Записати рiвняння прямої, що проходить через точку M(−2; 3; 4) |
|||||||||||||||||||||||||||||||||||||||
перпендикулярно до площини 3x − 2y + 5z − 6 = 0. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
Самостiйна робота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1. |
Знайти кут мiж прямими |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x −−2y −−3z − 1 = 0 |
та |
2 |
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||
|
2x 3y 4z + 5 = 0, |
|
|
x − 5 |
= |
y + 3 |
= |
z |
− 2 |
. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2x 3y + 4z 2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. |
Довести, що пряма x +−2y − 5z +−3 = 0 |
|
та площина |
|
|
|||||||||||||||||||||||||||||||||||
2x − 7y + 12z − 15 = 0 паралельнi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. |
Знайти проекцiю точки B(6; 1; 7) на площину 2x − y + 3z − 4 = 0. |
|||||||||||||||||||||||||||||||||||||||
4. |
Знайти проекцiю точки A(3; 2; 0) на пряму |
x − 2 |
= |
|
y + 2 |
= |
z − 5 |
. |
||||||||||||||||||||||||||||||||
|
4 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
−2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x + y + z |
2 = 0, |
|
|
||||||||||||
5. |
Записати канонiчне рiвняння прямої 2x − y − 3z−+ 6 = 0 . |
|||||||||||||||||||||||||||||||||||||||
6. |
Знайти точку перетину прямої та площини: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x − 2 |
= |
y − 3 |
|
= |
z + 1 |
, x + 2y + 3z 14 = 0. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
− |
1 |
|
− |
1 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7. |
Знайти точку M0, симетричну точцi M(0; −3; −2) вiдносно прямої |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x − 1 |
= |
y + 1, 5 |
|
= |
z |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
−1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8. |
Знайти точку M0, симетричну точцi M(1; 0; 1) вiдносно площини |
|||||||||||||||||||||||||||||||||||||||
4x + 6y + 4z − 25 = 0. |
|
|
|
x |
= |
y − 3 |
= |
z − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9. |
Показати, що пряма |
паралельна площинi |
||||||||||||||||||||||||||||||||||||||
6 |
−8 |
−9 |
||||||||||||||||||||||||||||||||||||||
x + 3y − 2z − 1 = 0, а пряма x = t + 7, y = t − 2, z = 2t лежить в цiй площинi.
10. При яких значеннях n та A пряма |
x |
= |
y − 5 |
= |
z + 5 |
перпендику- |
|
|
3 |
n |
|
||||
лярна до площини Ax + 2y − 2z − 7 = 0? |
|
6 |
|
||||
|
|
|
|
|
|
|
|
41

11. Довести, що наступнi прямi паралельнi
5 |
3 |
|
−1 |
та |
x −−2y − z +−2 = 0. |
||
x + 3 |
= |
y − 3 |
= |
z − 1 |
|
|
2x 3y + z 5 = 0, |
|
|
|
|
|
|||
12.Записати параметричне рiвняння медiани трикутника з вершинами A(3; 6; −7), B(−5; 1; −4), C(0; 2; 3), що проведена з вершини C.
13.При якому значеннi A площина Ax + 3y − 5z + 1 = 0 паралельна
прямiй |
x − 1 |
= |
y + 2 |
= |
z |
? |
4 |
|
|
||||
|
3 |
1 |
|
|||
14.Записати рiвняння прямої, що проходить через початок координат паралельно до прямої x = 2t + 5, y = −3t + 1, z = −7t − 4.
15.Перевiрити, чи лежать на однiй прямiй точки A(0; 0; 2), B(4; 2; 5)
та C(12; 6; 11).
16.Записати рiвняння прямої, що проходить через точку M(2; −3; 4)
перпендикулярно до прямих |
x + 2 |
= |
y − 3 |
= |
z + 1 |
|
та |
x + 4 |
= |
y |
= |
z − 4 |
. |
||||||||||||||||
|
1 |
−1 |
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
−3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3x |
y + 2z |
6 = 0, |
|
|
|
|
|||||||||||
17. |
При якому значеннi D пряма x +−4y − z +−D = 0 |
|
перетинає |
||||||||||||||||||||||||||
вiсь Oz? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
При якому значеннi p прямi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
y = −t + 2, та |
|
|
x y 3z 2 = 0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x = 2t + 5, |
|
|
|
|
− |
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
z = pt 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x + 3y + z + 2 = 0, |
|
|
|
|
|
|
|
||||||||||||
паралельнi? |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
19. |
Довести, що пряма |
x − 2 |
= |
y − 3 |
= |
z − 5 |
|
лежить в площинi |
|||||||||||||||||||||
x + 2y − 3z + 7 = 0. |
|
|
2 |
|
5 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x − 7 |
= |
y − 1 |
|
= |
z − 5 |
|
|
|
|
|
|||||||||||
20. |
Знайти точку перетину прямої |
|
|
|
та площини |
||||||||||||||||||||||||
|
1 |
|
|
||||||||||||||||||||||||||
3x − y + 2z − 8 = 0. |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
21. |
Записати |
загальне |
рiвняння |
прямої, що |
утворена |
перетином |
|||||||||||||||||||||||
площини x + 2y − z + 5 = 0 з площиною, що проходить через вiсь Oy та точку M(5; 3; 2).
22. При яких значеннях B та D пряма
x − 2y + z − 9 = 0, 3x + By + z + D = 0
лежить у площинi Oxy?
23.Записати рiвняння прямої, що проходить через точку E(3; 4; 5) паралельно Ox.
24.Записати рiвняння прямої, що проходить через точку M(2; 3; 1)
перпендикулярно до прямої |
x + 1 |
= |
y |
= |
z − 2 |
. |
2 |
−1 |
|
||||
|
|
3 |
|
|||
42

25. Записати канонiчне рiвняння прямої, що проходить через точку M(1; −5; 3) перпендикулярно до прямих
x = y − 2 = z + 1 та 2 3 −1
x = 3t + 1,
y = −t − 5,
z = 2t + 3.
ОСНОВИ МАТЕМАТИЧНОГО АНАЛIЗУ
§1. Границя функцiї. Перша особлива границя
Число A називається границею функцiї f(x) при x → a, якщо для будьякого як завгодно малого ε > 0 знайдеться таке δ > 0, що |f(x) − A| < ε
при 0 < |x − a| < δ. Цей факт записується так: lim f(x) = A.
x→a
При обчисленнi границь використовують такi властивостi: 1) lim [f(x) ± g(x)] = lim f(x) ± lim g(x);
x→a |
x→a |
x→a |
2) lim [f(x) · g(x)] = lim f(x) · lim g(x) ;
x→a |
x→a |
x→a |
|
f(x) |
|
lim f(x) |
|
3) lim |
= |
x→a |
||
|
||||
x→a g(x) |
|
lim g(x) |
||
|
|
|
x→a |
|
(при lim g(x) 6= 0).
x→a
Iнодi границю функцiї f(x) при x → a обчислити не вдається, оскiльки виникають невизначеностi типу 00 , ∞∞, ∞ − ∞, 0 · ∞ i т.п. В бiльшостi випадкiв цi невизначеностi можна розкрити за допомогою алгебраїчних перетворень.
При обчисленнi границь вiд тригонометричних функцiй часто використовують границю:
lim |
sin x |
= 1. |
(1) |
||
x |
|
||||
x→0 |
|
|
|||
Цю границю називають першою особливою границею.
Наведемо формули, якi використовуються при обчисленнi границь вiд тригонометричних функцiй
1 − cos 2α = 2 sin2 α;
43

cos α |
− |
cos β = |
− |
2 sin |
α + β |
sin |
α − β |
; |
|||||||||
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||
sin α + sin β = 2 sin |
|
α + β |
cos |
α − β |
; |
|
|
||||||||||
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
sin α |
− |
sin β = 2 sin |
|
α − β |
cos |
α + β |
. |
|
|
||||||||
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
Приклад 1. Обчислити границю |
|
lim |
x3 − 5x2 − 7 |
. |
|||||||||||||
|
|
|
|
|
|
|
x→∞ |
|
|
3x3 − 4 |
|
|
|||||
Розв’язання. Безпосередньо дану границю обчислити неможливо, ос-
кiльки маємо невизначенiсть типу ∞. Тому подiлимо чисельник та зна- |
|||||||||||||
3 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
менник на x . В результатi одержимо, що |
|
|
|
|
|
|
|
|
|
|
|||
lim |
x3 − 5x2 − 7 |
= lim |
1 − x5 − |
7 |
|
= |
|
1 |
. |
||||
x3 |
|||||||||||||
3x3 − 4 |
|
4 |
|
|
|
3 |
|||||||
x→∞ |
x→∞ |
|
3 − |
|
|
|
|||||||
|
x3 |
||||||||||||
Приклад 2. Обчислити границю lim |
|
x2 − 5x + 6 |
. |
|
|
|
|||||||
|
|
x→3 |
x2 − 9 |
|
|
|
|||||||
Розв’язання. Безпосередньо дану границю обчислити неможливо, ос-
кiльки маємо невизначенiсть типу 0 . Розкладемо чисельник та знаменник |
||||||||||||
на множники. Тодi |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
x2 − 5x + 6 |
= lim |
(x − 3)(x − 2) |
= lim |
x − 2 |
= |
1 |
. |
||||
x2 − 9 |
(x − 3)(x + 3) |
|
|
|||||||||
x→3 |
x→3 |
x→3 x + 3 |
|
6 |
||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
Приклад 3. Знайти границю lim |
x + 4 − 2 |
. |
|
|
|
|||||||
|
|
|
x→0 |
|
x |
|
|
|
|
|
|
|
Розв’язання. Маємо невизначенiсть типу 00 . Щоб її розкрити, помно-
жимо чисельник i знаменник на вираз, спряжений до чисельника: |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
√ |
|
|
− 2 |
= lim |
(√ |
|
|
|
− 2)(√ |
|
|
|
+ 2) |
|
|
|
|
|
|
||||||||||||
|
lim |
x + 4 |
x + 4 |
x + 4 |
= |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
x( x + 4 + 2) |
|
|
|
|
|
||||||||||||||||||||||
|
x |
→ |
0 |
|
|
|
→ |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x 0 |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= lim |
|
x + 4 − 4 |
|
= lim |
|
|
x |
|
= lim |
|
1 |
|
|
= |
|
1 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||||
x→0 x(√x − 2 + 2) |
|
x→0 x(√x + 4 + 2) |
|
x→0 √x + 4 + 2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
Приклад 4. Знайти границю x→2 |
x2 − 4 |
− |
x − 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
Розв’язання. Маємо невизначенiсть типу ∞ − ∞. Для її розкриття зведемо вираз, що стоїть в дужках до спiльного знаменника
x→2 x2 |
− 4 |
− x − 2 |
x→2 |
x2 − 4 |
x→2 x2 − 4 |
||||||
lim |
|
4 |
|
1 |
|
= lim |
4 − x − 2 |
|
= lim |
2 − x |
. |
|
|
|
|
|
|
|
|||||
44
Тепер маємо невизначенiсть 00 ; розкладаємо знаменник на множники:
|
x→2 x2 − 4 |
|
x→2 |
(x − 2)(x + 2) |
|
|
|
|
|
x→2 |
−x + 2 |
|
|
|
− |
4 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
2 − x |
|
|
= lim |
|
|
|
|
|
2 − x |
|
|
|
|
|
= lim |
|
|
|
|
|
1 |
|
|
|
|
|
|
= |
|
1 |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Приклад 5. Знайти границю lim |
1 − cos 5x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Розв’язання. |
|
Маємо невизначенiсть 00 . Виконаємо тригонометричнi |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
перетворення та використаємо першу особливу границю |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
−x2 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x→0 |
|
|
|
|
|
|
x→0 |
|
|
2 |
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
cos 5x |
|
|
|
|
|
|
|
2 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= 2 lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x→2 |
|
5 sin |
5 x |
|
2 |
x→0 |
|
|
5 |
|
2 |
|
|
|
|
· |
25 |
|
|
|
|
|
25 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
25 x |
2 |
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
= 2 lim |
|
|
|
|
|
|
|
|
|
|
|
|
= 2 lim |
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
= |
|
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аудиторнi завдання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Обчислити границi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
lim |
|
|
x3 + x + 2 |
; |
|
|
|
|
|
|
|
2. |
lim |
|
|
x4 + 5x3 + 7 |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2x3 + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
2x5 + 3x4 + 1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
3. |
lim |
|
|
2x4 + 5x − 6 |
; |
|
|
|
|
|
4. |
lim |
x2 − 6x + 8 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x→∞ x3 + 3x2 − 1 |
|
|
|
|
|
|
|
|
x→2 x2 − 8x + 12 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
x3 − 3x2 + 2 |
|
|
|
|
|
|
|
|
lim |
√ |
|
|
|
|
− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
5. |
lim |
|
; |
|
|
|
|
|
|
6. |
x + 13 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x→1 |
|
x2 − 7x + 6 |
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
x2 − 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
lim |
|
|
|
x + 7 |
− 3 |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
8. |
|
|
|
|
|
|
|
|
− 1−x3 ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x→2 |
|
√x + 2 − 2 |
|
|
|
|
|
|
|
|
x→1 1−x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
9. |
lim x( |
|
|
x2 |
+ 4 |
− |
x) |
; |
|
|
10. |
lim |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x→∞ |
|
|
|
p |
|
|
|
|
|
|
|
x→0 sin 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
11. |
lim |
1 − cos 6x |
; |
|
|
|
|
|
|
|
12. |
lim |
|
|
cos 5x − cos 3x |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x→0 |
|
|
|
x sin 3x |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
1 − cos x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Домашнi завдання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Обчислити границi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
xlim |
|
|
x4 + 5x3 + 7 |
; |
|
|
2. xlim |
|
|
|
|
|
x4+5x3+2 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2x |
5 |
+ 3x |
4 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
8 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
→∞ |
4x +2x |
+4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
45

|
|
|
|
|
2x2−3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
lim |
|
|
|
2x |
4. |
lim ( |
|
|
x2 |
+1 |
|
|
|
|
x2 |
− |
1) |
; |
||||||||||||||||
|
|
x+1 |
|
|
|
||||||||||||||||||||||||||||||
x→∞ |
− |
; |
x→∞ p |
|
|
−p |
|
|
|
|
|
||||||||||||||||||||||||
|
lim |
|
|
1 |
|
|
|
|
6 |
|
; |
|
lim |
x2 + 3x + 2 |
|
|
|
|
|
|
|
|
|||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
6. |
|
|
x3 + 1 |
; |
|
|
|
|
|
|
||||||||||||||
x→3 x−3 −x2−9 |
x→−1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x2 − 6x + 8 |
|
|
|
lim |
√ |
|
|
− 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
7. |
lim |
; |
|
8. |
x2 + 4 |
; |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x→2 x2 − 8x + 12 |
|
|
|
x→0 |
|
|
3x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
lim |
√ |
|
|
− 4 |
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
9. |
3x + 1 |
|
|
10. |
lim |
|
|
|
|
|
; |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x→5 3 − √x + 4 ; |
x→1 |
√3 + x2 − 2 |
|
|
|
|
|
||||||||||||||||||||||||||||
11. |
lim |
|
|
x tg x |
|
; |
|
|
|
12. |
lim |
1 − cos 8x |
; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x→0 |
|
1 − cos x |
|
|
|
x→0 |
1 − cos 4x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13. |
lim |
|
cos2 3x − cos2 x |
; |
14. |
lim |
sin(2(x − 1)) |
|
; |
|
|
|
|
||||||||||||||||||||||
|
x→0 |
|
|
|
|
|
x2 |
|
|
|
x→1 |
|
x2 − 7x + 6 |
|
|
|
|
|
|
|
|||||||||||||||
15.lim sin 5x · ctg 3x.
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Самостiйна робота |
|
|
|
||||||||||
Обчислити границi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
lim |
|
3x3 + 5x2 + 2 |
; |
|
|
2. |
lim |
|
5x4 − 3x2 + 7 |
; |
|
||||||||
|
2x3 + 5x2 − x |
|
|
|
|
|
|
|||||||||||||
|
x→∞ |
|
|
|
|
x→∞ x4 + 2x3 + 1 |
|
|
|
|||||||||||
3. |
lim |
|
3x2 + 2x + 9 |
; |
|
|
|
4. |
lim |
|
x5 − 2x + 4 |
; |
|
|||||||
|
2x2 − x + 4 |
|
|
|
|
2x4 + 3x2 + 1 |
|
|||||||||||||
|
x→∞ |
|
|
|
|
|
x→∞ |
|
|
|
||||||||||
5. |
lim |
|
3x2 + 7x − 4 |
; |
|
|
|
6. |
lim |
|
x7 + 5x2 − 4x |
; |
|
|||||||
|
|
|
|
|
|
|
|
|
3x2 + 11x − 7 |
|
||||||||||
|
x→∞ x5 + 2x − 1 |
|
|
|
|
|
x→∞ |
|
|
|
||||||||||
7. |
lim |
x3 − x2 + 2x |
; |
|
|
|
|
8. |
lim |
2x2 − x − 1 |
; |
|
|
|
|
|||||
|
x→0 |
|
|
x2 + x |
|
|
|
|
|
x→1 |
3x2 − x − 2 |
|
|
|
||||||
9. |
lim |
12 + x − x2 |
; |
|
|
|
|
10. |
lim |
|
2x2 + 11x + 15 |
; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x→3 |
|
x3 − 27 |
|
|
|
|
|
x→−3 3x2 + 5x − 12 |
|
||||||||||
11. |
lim |
|
3x2 + 2x + 1 |
; |
|
|
|
12. |
lim |
|
2x2 − 3x − 1 |
; |
|
|
|
|||||
|
|
x3 − 8 |
|
|
|
|
|
|
|
|
||||||||||
|
x→2 |
|
|
|
|
|
|
x→1 |
|
x4 − 1 |
|
|
|
|||||||
13. |
lim |
|
x4 − x2 + x + 1 |
; |
14. |
lim |
|
2x2 + 7x − 4 |
; |
|
||||||||||
|
x→−1 x4 − 1 |
|
|
|
|
|
x→−4 x3 + 64 |
|
|
|
||||||||||
15. |
lim |
|
|
x3 + x − 2 |
|
; |
|
16. |
lim |
|
4x4 − 5x2 + 1 |
; |
|
|||||||
|
x→1 x3 − x2 − x + 1 |
|
x→1 |
|
x2 − 1 |
|
|
|
||||||||||||
46
17. |
lim |
4x3 − 2x2 + 5x |
; |
|
|||||||||||||
|
x→0 |
|
|
3x2 + 7x |
|
|
|
|
|
|
|
||||||
19. |
|
lim |
8x3 − 1 |
; |
|
|
|
|
|
|
|
||||||
|
x→1/2 |
x2 − 41 |
|
|
|
|
|
|
|
||||||||
21. |
lim |
|
|
x3 − 64 |
|
|
|
|
; |
|
|
||||||
7x2 − 27x − |
|
4 |
|
|
|||||||||||||
|
x→4 |
|
|
|
|
||||||||||||
|
|
|
|
√ |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
23. |
lim |
|
|
x+12− 4−x |
; |
||||||||||||
|
x→−4 |
|
x2+2x |
|
8 |
|
|
|
|||||||||
|
|
|
|
√ |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|||
25. |
lim |
|
x2 + 2 − |
|
2 |
; |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→0 |
√x2 |
+ 1 − 1 |
|
|
|||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
27. |
lim |
|
x − 3 |
− 2 |
|
|
|
|
|
|
|
||||||
x→7 |
√x + 2 − 3 ; |
|
|
|
|
|
|
|
|||||||||
|
|
√ |
|
− 5 |
|
|
|
|
|
|
|
||||||
29. |
lim |
2x + 7 |
; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
x→9 |
√ |
3 − √x |
|
|
|
|
|||||||||||
|
|
|
− 1 |
; |
|
||||||||||||
31. |
lim |
1 + 3x2 |
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
x→0 |
|
|
x3 + x2 |
|
|
|
|
|
|
|
||||||
|
lim |
3x2 |
− 2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
33. |
√ |
|
|
; |
|
|
|
|
|
|
|
||||||
x |
→ |
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
√ |
8 + x − 3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35. |
lim |
|
4x + 1 − 3 |
; |
|
|
|
|
|||||||||
|
x→2 |
|
|
x3 − 8 |
|
|
|
|
|
|
|
||||||
p
37.lim ( x2 + 4 − x);
x→∞
√√
18. |
lim |
x2 − x − 30 |
|
; |
|
||||||||||||||
|
x→−5 x3 + 125 |
|
|
|
|
||||||||||||||
20. |
lim |
x3 − 2x − 4 |
|
|
|
; |
|||||||||||||
|
x→2 x2 − 11x + 18 |
||||||||||||||||||
|
lim |
|
x2+x−12 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
22. |
x→3 |
√x 2 |
√4 |
− |
x; |
||||||||||||||
|
|
|
|
|
− − |
|
|
|
|
|
|||||||||
|
|
2 − |
√ |
|
|
|
|
|
|
|
; |
|
|
|
|||||
24. |
lim |
x2 + 4 |
|
|
|
||||||||||||||
3x2 |
|
|
|
|
|
||||||||||||||
|
x→0 |
√ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
− 3 |
|
|
|
|
||||||
26. |
lim |
2x + 1 |
|
|
; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→4 |
√ |
x − 2 |
− |
√2 |
|
|
|||||||||||||
|
|
√ |
|
|
|
|
|
− 2 |
|
|
|
|
|||||||
28. |
lim |
x2 + 4 |
|
|
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x→0 |
√x2 + 16 − 4 |
||||||||||||||||||
30. |
lim |
x3 − 27 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x; |
|
|
|
|
|
|
|||||||
x→3 |
√3x |
− |
|
|
|
|
|
|
|||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
||||
32. |
lim |
|
|
x + 20 − 4 |
; |
||||||||||||||
|
x→−4 |
x3 + 64 |
|
|
|
|
|||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. |
lim |
|
9 + x − 3 |
; |
|
|
|
|
|||||||||||
|
x→0 |
|
x2 + x |
|
|
|
|
|
|
||||||||||
|
|
|
√ |
|
− 2 |
|
|
|
|
|
|
||||||||
36. |
lim |
|
x |
|
; |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
→ |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2x + 1 − 3 |
|
|
|
|
|||||||||||
pp
38.lim ( x2+1− x2−9);
x→∞
p
39. |
xlim ( |
|
|
x + 9 − |
|
x − 1); |
40. |
xlim (x − |
x2 + 9); |
|
|
|
||||||||||||||||||
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
41. |
x→∞ p |
|
|
|
|
|
|
− |
|
; |
|
42. |
x→∞ |
|
|
− p |
|
|
|
|
|
|
|
; |
||||||
|
lim ( x2+4x+2 x) |
|
|
|
lim (x |
|
|
|
x2 |
+ 5x + 3) |
|
|||||||||||||||||||
43. |
lim |
5x |
− |
2+5x2 |
; |
|
|
|
44. |
lim |
|
6x2 − 1 |
− |
2x |
|
|
|
|||||||||||||
|
x−4 |
|
|
|
|
2 + 3x |
|
|
|
|||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
x→∞ |
|
; |
|
|
|
||||||||||||||||
45. |
lim |
x |
|
|
|
x3 − x2 + 2 |
; |
46. |
lim |
|
|
1 |
|
|
2 |
|
; |
|
|
|
||||||||||
|
− |
|
|
|
1−x− |
1−x2 |
|
|
|
|||||||||||||||||||||
x→∞ |
|
|
|
|
x2 + 1 |
|
|
x→1 |
|
|
|
|||||||||||||||||||
47. |
lim |
|
x2+1 |
|
x2+2x |
; |
48. |
lim |
|
|
2 |
|
|
|
|
|
1 |
|
; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
− 3x+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x→∞ x−1 |
x→5 x − 5 − x2 − 25 |
|
||||||||||||||||||||||||||||
47

49. |
lim |
1 − cos 8x |
; |
|
|
|
|
||||||||||
|
x→0 |
|
3x2 |
|
|
|
|
|
|
|
|
|
|||||
51. |
lim |
cos x − cos 5x |
; |
|
|||||||||||||
|
x→0 |
|
|
2x2 |
|
|
|||||||||||
53. |
|
lim |
1 − sin x |
; |
|
|
|
||||||||||
|
x→π/2 |
π − 2x |
|
|
|||||||||||||
55. |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|||||
x→0 tg x − sin x ; |
|||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin 7x + sin 3x |
|
|
||||||||||||||
57. |
lim |
; |
|
||||||||||||||
|
x sin x |
||||||||||||||||
|
x→0 |
|
|
|
|||||||||||||
59. |
lim |
cos 4x − cos3 4x |
; |
||||||||||||||
|
x→0 |
|
|
|
3x2 |
|
|
||||||||||
61. |
lim |
1 − cos 4x |
; |
|
|
||||||||||||
|
x→0 |
|
sin2 3x |
|
|
||||||||||||
63. |
lim tg2 3x |
· |
ctg2 2x |
; |
|
||||||||||||
x |
→ |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim |
|
sin2 3x |
|
|
||||||||||||
65. |
|
|
|
|
|
; |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
x→0 arctg2 |
2x |
|
|
|||||||||||||
50. |
lim |
sin 3x − sin x |
; |
|
|
||||||||||
|
x→0 |
|
|
5x |
|
|
|
|
|
|
|
|
|||
52. |
lim |
tg x − sin x |
; |
|
|
|
|||||||||
|
x→0 |
|
|
3x2 |
|
|
|
|
|
|
|
|
|||
54. |
lim |
1 − cos2 x |
; |
|
|
|
|
||||||||
|
x→0 |
|
x tg x |
|
|
|
|
|
|
|
|
||||
56. |
lim |
sin2 3x − sin2 x |
; |
||||||||||||
|
|
x2 |
|||||||||||||
|
x→0 |
|
|
|
|
||||||||||
58. |
|
lim |
1 − sin 2x |
; |
|
|
|
||||||||
|
x→π/4 |
|
π − 4x |
|
|
||||||||||
60. |
lim |
cos2 x − cos2 2x |
; |
||||||||||||
|
x→0 |
√ |
|
x2 |
|
|
|||||||||
62. |
lim |
x |
|
1 − cos 4x |
; |
|
|
||||||||
|
|
|
|
||||||||||||
|
x→0 |
|
sin2 3x |
|
|
||||||||||
64. |
lim |
|
sin 5x |
|
; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x→0 arcsin 2x |
|
|
||||||||||||
66. |
lim sin2 3x |
· |
ctg2 5x |
. |
|||||||||||
x |
→ |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§2. Друга особлива границя. Неперервнiсть функцiї
Другою особливою границею називають границю: |
|
|||||||
1 |
|
x |
|
|
1 |
|
|
|
lim |
|
|
lim (1 + x) x = e, |
(1) |
||||
|
||||||||
x→∞ 1 + x |
= x→0 |
|
|
|
|
|
||
де e – число Ейлера (e ≈ 2, 718281828). |
2x + 1 |
|
3x+1 |
|
||||
|
|
|
|
|
|
|||
|
|
|
lim |
|
|
. |
|
|
|
|
|
2x − 1 |
|
||||
Приклад 1. Знайти границю x→∞ |
|
|||||||
Розв’язання. Безпосередньо дану границю обчислити неможливо, оскiльки маємо невизначенiсть типу 1∞. Тому алгебраїчними перетвореннями зведемо дану границю до вигляду другої особливої границi
lim |
|
2x + 1 |
|
3x+1 |
= lim |
|
2x − 1 + 2 |
|
3x+1 |
= |
2x − 1 |
|
2x − 1 |
|
|||||||
x→∞ |
|
x→∞ |
|
|
48

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2−1 |
|
|
2 |
·(3x+1) . |
||||||||||||
= xlim |
|
1 + |
|
2x |
2 |
|
1 |
3x+1 |
= xlim |
1 + |
2x |
2 |
|
|
1 |
|
|
|
|
2x−1 |
||||||||||||||||||||||||||||||||||||||||
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
→ 0 при x → ∞, то 1 + |
2 |
|
|
|
2x−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Так як |
|
|
|
|
|
|
2 |
→ e, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
2x |
|
− |
|
1 |
2x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
а x→∞ |
|
2x |
|
1 |
|
|
= x→∞ |
2x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
2x |
|
1 |
|
|
3x+1 |
. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. Тому x→∞ |
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
lim |
2(3x + 1) |
|
|
lim |
6x + 2 |
= 3 |
|
|
|
|
|
|
lim |
|
|
|
|
2x + 1 |
|
|
|
|
|
|
|
= e3 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
+ 5x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − 3x + 7 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
Приклад 2. Обчислити границю x→∞ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Розв’язання. Використаємо другу особливу границю |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 + 5x + 4 |
|
|
x |
|
|
x→∞ |
|
|
|
x2 + 5x + 4 |
− |
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
x→∞ x2 − 3x + 7 |
|
|
|
|
|
x2 − 3x + 7 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= |
|
|
|
|
|
|||||||||||||||||
= lim |
1 + |
x2 + 5x + 4 − x2 + 3x − 7 |
|
x |
= lim |
|
|
1 + |
|
|
|
|
8x − 3 |
|
|
|
x |
= |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 − 3x + 7 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
x2 − 3x + 7 |
|
|
|
|
|
|
|
|
|
x→∞ |
− |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
3) x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
x −3x+7 |
x −3x+7 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
= lim |
|
1 + |
|
|
|
8x − |
3 |
|
|
|
|
8x−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→∞ x2 − 3x + 7 |
|
|
, тому |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x |
|
−3x+7 |
→ . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
− 3x + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
lim |
|
8x |
− |
3 |
|
|
|
= 0 |
|
|
|
|
|
|
1 + |
|
|
8x |
− 3 |
|
|
|
|
|
|
8x−3 |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
lim |
|
8x2 − 3x |
|
= |
|
lim |
|
|
|
|
8 − 3/x |
|
|
= 8. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x→∞ x2 − 3x + 7 |
|
x→∞ 1 − 3/x + 7/x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Таким чином, lim x2 + 5x + 4 x = e8. x→∞ x2 − 3x + 7
Функцiя f(x) називається неперервною в точцi x0 D(f), якщо вона визначена в деякому околi цiєї точки i lim f(x) = f(x0).
|
lim |
|
|
f(x) = lim f(x) = f(x0 + 0) (правостороння границя), |
|||||
x→x0+0 |
x→x0 |
|
|
|
|
||||
|
|
|
|
|
x>x0 |
|
|
|
|
|
lim |
|
lim f(x) = f(x |
0 − |
0) |
(лiвостороння границя) |
, |
||
x |
→ |
x0 |
− |
0 f(x) = x x0 |
|
|
|||
|
|
|
→ |
|
|
|
|
||
x<x0
49
то означення неперевностi функцiї f(x) в точцi x0 можна записати так:
lim f(x) = |
lim f(x) = |
|
lim f(x). |
(2) |
|||
x→x0 |
x→x0−0 |
|
|
x→x0+0 |
|
||
Розглянемо види розривiв. |
lim |
0 f(x)=f(x0 |
− 0) та |
||||
1. Якщо iснують скiнченнi границi x |
|||||||
→ |
x0 |
− |
|||||
|
|
|
|
|
|||
lim f(x) = f(x0 + 0), причому всi три значення f(x0), f(x0 − 0),
x→x0+0
f(x0 + 0) не рiвнi мiж собою, то x0 називається точкою розриву першого роду. Зокрема:
а) якщо f(x0 − 0) = f(x0 + 0) 6= f(x0), то x0 – точка усувного розриву;
б) якщо f(x0 − 0) 6= f(x0 + 0), то x0 – точка розриву першого роду типу "стрибок".
2. Якщо хоча б одна з границь f(x0 − 0) або f(x0 + 0) не iснує (або дорiвнює ±∞), то x0 називається точкою розриву другого роду.
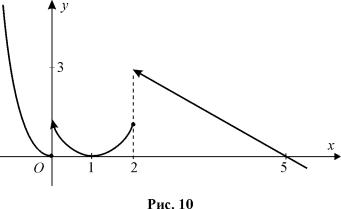
Приклад 3. |
Дослiдити функцiю на неперервнiсть та побудувати її |
||||||
графiк, якщо f(x) = |
(x |
1)2 |
, 0 < x ≤ 2, |
||||
|
|
|
x2 |
, −∞ |
< x ≤ 0, |
||
|
|
5 |
|
−x, |
2 |
< x < + . |
|
|
|
|
|
− |
|
∞ |
|
Розв’язання. |
Функцiя f(x) визначена i неперервна на iнтервалах |
||||||
|
|
|
|
|
|
|
|
(−∞; 0), (0; 2), (2; +∞). Тому розриви можуть бути в точках x1=0, x2=2.
В точцi x1 = 0 |
|
|
|
|
|
|
|
|
|
|
lim f(x) = |
x |
lim |
x2 = 0; |
lim f(x) = |
x |
lim |
2 = 1. |
|||
x 0 |
0 |
0 |
− |
0 |
x 0+0 |
→ |
0+0(x − 1) |
|
||
→ − |
|
|
→ |
|
→ |
|
|
|
||
50
