
Рудницький В.Б._ Вища матем в правах и задачах
.pdf
2. Нехай прямi заданi рiвняннями з кутовими коефiцiєнтами:
y = k1x + b1 та y = k2x + b2. Тодi тангенс кута ϕ мiж прямими обчислюється за формулою:
tg ϕ = |
k2 − k1 |
. |
(4) |
Умова паралельностi має вигляд: |
1 + k1 · k2 |
|
|
|
|
|
|
k1 = k2, |
(5) |
||
а умова перпендикулярностi – |
|
|
|
k1 · k2 = −1. |
(6) |
||
Вiдстань d вiд точки M(x0, y0) до прямої, що задається загальним рiвнянням Ax + By + C = 0, визначається за формулою:
|
|
d = |
|Ax0 + By0 + C| |
. |
(7) |
||||
|
|
|
|
|
|||||
|
|
|
√A2 + B2 |
|
|||||
Приклад 1. Знайти вiдстань мiж двома паралельними прямими |
|
||||||||
√ |
|
|
√ |
|
|
|
|||
3x + y − 3 10 = 0 та 6x + 2y + 5 10 = 0.
Розв’язання. Задача зводиться до визначення вiдстанi вiд довiльної
точки однiєї прямої до другої прямої. Поклавши, наприклад, у рiвняннi
√ √
першої прямої x=0, отримаємо, що y=3 10. Таким чином, M(0; 3 10) – точка, що лежить на першiй прямi. Тепер визначимо вiдстань вiд точки
M до другої прямої |
|
|
|
|
|
|
|
|
|
|||||
|
|6 · 0 + 2 · 3√ |
|
+ 5√ |
|
| |
= |
11√ |
|
|
|
|
|||
d = |
10 |
10 |
10 |
|
5, 5. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
√62 + 22 |
|
|
2√10 |
≈ |
||||||||||
|
|
|
|
|
||||||||||
Приклад 2. Визначитии гострий кут мiж прямими y = −3x + 7 та y = 2x + 1.
Розв’язання. Використаємо формулу (4), поклавши k1= − 3, k2=2.
Тодi |
|
1 + ( |
3) |
2 |
|
|
|
|
5 |
|
|
тобто |
|
4 |
|
tg ϕ = |
|
2 − |
(−3) |
|
|
= |
|
5 |
|
= 1, |
|
ϕ = |
π |
. |
|
|
− · |
|
− |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 3. Довести, що прямi 3x − 5y + 7 = 0 та 10x + 6y − 3 = 0 перпендикулярнi.
Розв’язання. З рiвняння першої прямої маємо: A1=3, B1= − 5, для другої прямої A2 = 10, B2 = 6. За формулою (2) A1A2 + B1B2 = = 3 · 10 + (−5) · 6 = 0, тобто прямi перпендикулярнi.
31

Aудиторнi завдання
1. Точка A(2; −5) є вершиною квадрата, одна з сторiн якого лежить на прямiй x − 2y − 7 = 0. Обчислити площу квадрата.
2.Обчислити значення меншого кута ϕ мiж прямими 3x + 4y − 2 = 0
та 8x + 6y + 5 = 0.
3.Визначити, при якому значеннi m рiвняння 3mx − 2y + 5 = 0 та 2x + 9y − 7 = 0 задають: а) паралельнi прямi; б) перпендикулярнi прямi.
4.Дослiдити взаємне розташування двох прямих `1 та `2. Якщо `1 та `2 паралельнi, то знайти вiдстань мiж ними та точку перетину:
a) |
`1: −2x + y − 1 = 0, |
`2: |
2y + 1 = 0; |
||||||
|
`1: x + y − 1 = 0, |
|
x |
= |
y + 1 |
||||
б) |
`2: |
|
|
|
|
|
. |
||
2 |
|
−2 |
|||||||
Домашнi завдання
1.Записати рiвняння трьох сторiн квадрата, якщо вiдомо, що четвертою стороною є вiдрiзок прямої 4x + 3y − 12 = 0, кiнцi якого лежать на осях координат.
2.Знайти рiвняння прямої, що проходить паралельно до прямої
12x + 5y − 52 = 0 на вiдстанi 2 вiд неї. |
√3y+1 = 0, |
√3x+y+1 = 0 |
3. Довести, що трикутник iз сторонами x+ |
та x − y − 10 = 0 рiвнобедрений. Знайти кут при його вершинi. 4. Довести, що наступнi пари прямих паралельнi:
a)2x + 3y − 3 = 0 та 4x + 6y + 1 = 0; б) y = 2x − 3 та y = 2x + 5.
5.Доведiть, що наступнi пари прямих взаємно перпендикулярнi:
a)2x + 3y + 1 = 0 та 6x − 4y + 3 = 0;
б) x + 2y − 3 = 0 та 6x − 3y + 5 = 0.
Самостiйна робота
1.Записати рiвняння прямoї, що проходить через точку перетину прямих 3x − 2y − 7 = 0 i x + 3y − 6 = 0 та вiдтинає на осi абсцис вiдрiзок, рiвний 5.
2.Знайти проекцiю точки A(−8; 12) на пряму, що проходить через точки B(2; −3) та C(−5; 1).
3.Дано двi вершини трикутника ABC: A(−4; 4), B(4; −12) та точка M(4; 2) перетину його висот. Знайти вершину C.
4.Визначити вiдстань вiд точки M(2; −1) до прямої, що вiдтинає на осях координат вiдрiзки a = 8, b = 6.
32
5.При якому значеннi m прямi 7x − 2y − 5 = 0, x + 7y − 8 = 0 та mx + my − 8 = 0 перетинаються в однiй точцi?
6.Точки A(1; 2) та B(3; 6) – протилежнi вершини квадрата. Визначити координати двох iнших вершин.
7.Знайти пряму, що проходить через точку перетину прямих x + 2y + 3 = 0, 2x + 3y + 4 = 0 паралельно до прямої 5x + 8y = 0.
8.Знайти пряму, що проходить через точку перетину прямих
x + 2y + 1 = 0, 2x + y + 2 = 0 та утворює кут 1350 з вiссю абсцис.
9.Довести, що чотирикутник ABCD – трапецiя, якщо A(3; 6), B(5; 2),
C(−1; −3), D(−5; 5).
10.Запишiть рiвняння прямої, що проходить через точку A(3; 1) перпендикулярно до прямої BC, якщо B(2; 5), C(1; 0).
11.Знайти точку, симетричну точцi M(2; −1) вiдносно прямої x − 2y + 3 = 0.
12.Знайти точку O перетину дiагоналей чотирикутника ABCD, якщо
A(−1; −3), B(3; 5), C(5; 2), D(3; −5).
13.Вiдомо рiвняння сторони AB трикутника ABC: 4x + y = 12, його висот BH: 5x − 4y = 12 та AM: x + y = 6. Знайти рiвняння двох iнших сторiн трикутника ABC.
14.Дано двi вершини трикутника ABC: A(−6; 2), B(2; −2) та точка перетину його висот H(1; 2). Знайти координати точки M перетину сторони AC та висоти BH.
15.Обчислити координати точки перетину серединних перпендикулярiв сторiн трикутника з вершинами A(2; 3), B(0; −3), C(6; −3).
16.Записати рiвняння висоти, проведеної з вершини A трикутника ABC, якщо вiдомi рiвняння його сторiн AB: 2x−y−3=0, AC: x+5y−7=0,
BC: 3x − 2y + 13 = 0.
17.Дано трикутник з вершинами A(3; 1), B(−3; −1), C(5; −12). Знайти рiвняння та обчислити довжину його медiани, проведеної з вершини
C.
18.Знайти рiвняння перпендикулярiв до прямої 3x + 5y − 15 = 0, проведених через точки перетину даної прямої з осями координат.
19.Дано рiвняння сторiн чотирикутника: x−y=0, x+3y=0, x−y−4=0, 3x + y − 12 = 0. Знайти рiвняння його дiагоналей.
20.Записати рiвняння прямої, що проходить через точку A(−2; 3) та утворює з вiссю Ox кут: а) 450; б) 900; в) 00.
21.Через точку перетину прямих 2x − 5y − 1 = 0 та x + 4y − 7 = 0 провести пряму, що дiлить вiдрiзок мiж точками A(4; −3) та B(−1; 2) у вiдношеннi λ = 2/3.
33
22.Вiдомi рiвняння двох сторiн ромба 2x−5y −1 = 0 i 2x−5y −34 = 0 та рiвняння однiєї з його дiагоналей x+3y−6 = 0. Знайти рiвняння другої дiагоналi.
23.Знайти точку E перетину медiан трикутника ABC, якщо A(−3; 1),
B(7; 5), C(5; −3).
24.Дано рiвняння двох сторiн паралелограма x −2y = 0, x −y −1 = 0 та точка перетину його дiагоналей M(3; −1). Знайти рiвняння двох iнших сторiн.
§3. Площина
Площина в декартовiй прямокутнiй системi координат Oxyz може бути задана наступними рiвняннями:
1. Загальне рiвняння площини:
Ax + By + Cz + D = 0, (1)
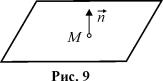
де A, B, C координати нормального, тобто перпендикулярного до площини вектора ~n (рис.9).
2. Рiвняння площини, що задається точкою M(x0, y0, z0) та нормальним вектором ~n = {A, B, C} (рис.9):
A(x − x0) + B(y − y0) + C(z − z0) = 0. |
(2) |
|||||||
3. Рiвняння площини у "вiдрiзках": |
|
|
||||||
x |
+ |
y |
+ |
z |
= 1, |
(3) |
||
|
a |
|
b |
c |
||||
|
|
|
|
|
||||
де a, b, c – вiдрiзки, що вiдтинає площина на координатних осях Ox, Oy i Oz вiдповiдно.
4. Рiвняння площини, що проходить через три заданi точки
M1(x1, y1, z1), M2(x2, y2, z2) та M3(x3, y3, z3):
|
x2 |
− x11 |
y2 |
− y1 |
||||
|
x |
x |
|
y |
y1 |
|||
x |
3 |
− x |
1 |
y |
3 |
− y |
1 |
|
|
|
− |
|
− |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
z − z1 z2 − z1 z3 − z1
= 0. (4)
34

5. Рiвняння площини, що проходить через задану точку M1(x1, y1, z1)
паралельно двом заданим векторам ~a = {ax, ay, az} |
~ |
|||||||
та b = {bx, by, bz}: |
||||||||
|
ax |
ay |
az |
= 0. |
(5) |
|||
|
x − x1 |
y − y1 |
z − z1 |
|
|
|||
b |
x |
b |
y |
b |
z |
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай двi площини заданi рiвняннями у загальному виглядi:
A1x + B1y + C1z + D1 = 0, A2x + B2y + C2z + D2 = 0.
Косинус кута ϕ мiж двома площинами обчислюється за формулою:
cos ϕ = |
|
A1A2 + B1B2 |
+ C1C2 |
, |
(6) |
|||
|
|
|
|
|
||||
pA12 + B12 + C12 · |
pA22 + B22 + C22 |
|||||||
|
|
|
||||||
де ~n1 = {A1, B1, C1} та ~n2 = {A2, B2, C2} – нормальнi вектори даних площин.
Умова паралельностi двох площин:
A1 |
= |
B1 |
= |
C1 |
6= |
D1 |
(7) |
|||
|
|
|
|
|
|
. |
||||
A2 |
B2 |
C2 |
D2 |
|||||||
Умова перпендикулярностi двох площин:
A1 · A2 + B1 · B2 + C1 · C2 = 0. |
(8) |
Вiдстань d вiд точки M(x0, y0, z0) до площини Ax + By + Cz + D = 0 обчислюється за формулою:
d = |
|Ax0 + By0 + Cz0 + D| |
. |
(9) |
||
|
|
|
|||
|
√A2 + B2 + C2 |
|
|||
Аудиторнi завдання
1.Записати рiвняння площини:
a)що проходить через точку M(7; −3; 5) паралельно площинi Oxz;
б) що проходить через вiсь Oz та точку A(−3; 1; −2);
в) що проходить через двi точки M1(4; 0; −2) та M2(5; 1; 7) паралельно осi Ox;
г) що проходить через точку M(7; −5; 1) та вiдтинає на осях координат рiвнi додатнi вiдрiзки.
2. Знайти кут мiж площинами x − 2y + 2z − 3 = 0 та 3x − 4y + 5 = 0.
35
3.Обчислити вiдстань мiж паралельними площинами
3x + 6y + 2z−15=0 та 3x + 6y + 2z + 13 = 0.
4.Дослiдити взаємне розташування площин:
а) −x + 2y − z + 1 = 0 та y + 3z − 1 = 0;
б) 2x − y + z − 1 = 0 та −4x + 2y − 2z − 1 = 0; в) 2x − y − z + 1 = 0 та x + 4y − 2z + 5 = 0.
Домашнi завдання
1.Записати рiвняння площини, що проходить через точку P (1; 0; 2) перпендикулярно до двох площин 2x−y+3z −1 = 0 та 3x+6y+3z −5 = 0.
2.Записати рiвняння площини, що проходить паралельно вектору
~ |
−1} та вiдтинає на осях Ox та Oy вiдрiзки a = 3, b = −2. |
S = {2; 1; |
3.Записати рiвняння площини, що проходить через лiнiю перетину площин x + 5y + 9z − 13 = 0, 3x − y − 5z + 1 = 0 та через точку M(0; 2; 1).
4.Запишiть рiвняння площини, що проходить паралельно площинi 2x − 6y + 3z − 56 = 0 на вiдстанi d = 4.
5.Знайдiть кут мiж площинами 2x + y − 2z + 3 = 0 та x + y − 5 = 0.
Самостiйна робота
1.Знайти вiдрiзки, якi вiдтинає на координатних осях площина, що проходить через точку M(−2; 7; 3) паралельно площинi x−4y +5z −1 = 0.
2.Записати рiвняння площини, що проходить через середину вiдрiзка M1M2 перпендикулярно до нього, якщо M1(1; 5; 6), M2(−1; 7; 10).
3.Знайти довжину перпендикуляра, проведеного з точки M(2; 3; −5) до площини 4x − 2y + 5z − 12 = 0.
4. Записати рiвняння площини, що проходить через точки A(2; 5; 1) та B(−3; 1; 3) паралельно осi Oy.
5. Записати рiвняння площини у "вiдрiзках", якщо вона проходить через точку M(6; −10; 1) та вiдтинає на осi Ox вiдрiзок a = −3, а на осi Oz – вiдрiзок c = 2.
6.Знайти рiвняння площини, точки якої рiвновiддаленi вiд точок
P (1; −4; 2) та Q(7; 1; −5).
7.Знайти рiвняння площини, що проходить через точку перетину площин 2x + 2y + z − 7 = 0, 2x − y + 3z − 3 = 0, 4x + 5y − 2z − 12 = 0 та через точки M(0; 3; 0) i N(1; 1; 1) .
8. Записати рiвняння площини, що проходить через точки A(1; 1; 0) та B(2; −1; −1) перпендикулярно до площини 5x + 2y + 3z − 7 = 0.
36

9.Записати рiвняння площини, що проходить через початок координат перпендикулярно до двох площин 2x−3y+z−1 = 0 та x−y+5z+3 = 0.
10.Записати загальне рiвняння площини, що проходить через поча-
~ |
−2; 3), |
ток координат перпендикулярно вектору AB, якщо A(5; |
B(1; −3; 5).
11.Записати загальне рiвняння площини, що проходить через точку A(3; −4; 1) паралельно координатнiй площинi Oxz.
12.Визначити, при якому значеннi B площини x − 4y + z − 1 = 0 та 2x + By + 10z − 3 = 0 перпендикулярнi.
13.Обчислити об’єм пiрамiди, обмеженої площиною
2x − 3y + 6z − 12 = 0 та координатними площинами.
14.Записати рiвняння площини, рiвновiддаленої вiд двох площин:
4x − y − 2z − 3 = 0 та 4x − y − 2z − 5 = 0.
15.Визначити при якому значеннi C площини 3x −5y + Cz −3 = 0 та x − 3y + 2z + 5 = 0 перпендикулярнi.
16.При яких значеннях B та N площини 2x + y + Bz − 1 = 0 та
Nx + 3y + 15z + 5 = 0 паралельнi?
17.Записати рiвняння площини, що проходить через точки
M(2; 3; −5) та N(−1; 1; −6) паралельно вектору ~a = {4; 4; 3}.
18.Знайти кут мiж площинами x − 2y + 2z + 3 = 0 та x + z − 5 = 0.
19.Записати рiвняння площини, що проходить через лiнiю перетину площин 2x − y − 12z − 3 = 0 i 3x + y − 7z − 2 = 0 перпендикулярно до
площини x + 2y + 5z − 1 = 0.
− ~ ~ ~
20. Який кут утворює з площиною x+y+2z 4 = 0 вектор ~a = i+2j+k?
§4. Пряма в просторi. Пряма та площина
В залежностi вiд способу задання прямої в просторi можна розглядати рiзнi її рiвняння.
1. Загальне рiвняння прямої в просторi як перетин двох площин:
A1x + B1y + C1z + D1 |
= 0, |
(1) |
|
A2x + B2y + C2z + D2 = 0. |
|||
|
|||
2. Рiвняння прямої, що проходить через двi точки M1(x1, y1, z1) та
M2(x2, y2, z2):
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
(2) |
x2 − x1 |
|
y2 − y1 |
|
z2 − z1 |
|
|
37
3. Канонiчне рiвняння прямої: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
, |
(3) |
||||||||
|
|
|
m |
|
|
n |
|
|
|
p |
|
|
|
|
||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
||||
де M(x0, y0, z0) – точка, що лежить на прямiй; S = {m, n, p} – напрямний |
||||||||||||||||
вектор прямої. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Параметричне рiвняння прямої, що проходить через точку |
||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
M(x0, y0, z0) i має напрямним вектор S = {m, n, p}: |
|
|
|
|||||||||||||
|
|
|
y = y0 |
+ nt, |
|
(4) |
||||||||||
|
|
|
|
|
x = x0 |
+ mt, |
|
|
|
|
||||||
|
|
|
z = z0 + pt. |
|
|
|
|
|||||||||
Нехай двi прямi в просторi |
задаються канонiчними рiвняннями |
|||||||||||||||
x − x1 |
= |
y − y1 |
= |
z − z1 |
, |
x − x2 |
= |
y − y2 |
= |
z − z2 |
. |
|||||
m1 |
|
n1 |
p1 |
|
m2 |
n2 |
|
p2 |
||||||||
Косинус кута ϕ мiж двома прямими в просторi визначається за
формулою: |
|
|
|
m1 · m2 + n1 · n2 + p1 · p2 |
|
|
|||||||||||
|
cos ϕ = |
|
|
. |
(5) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
m12 + n12 + p12 · m22 + n22 + p22 |
|
|||||||||||
Умова |
перпендикулярностi двох прямих у просторi: |
|
|||||||||||||||
|
|
p |
|
|
|
|
p |
|
|
|
|
||||||
|
|
m1 · m2 + n1 · n2 + p1 · p2 = 0. |
(6) |
||||||||||||||
Умова паралельностi двох прямих у просторi: |
|
||||||||||||||||
|
|
|
|
|
|
m1 |
= |
n1 |
= |
p1 |
. |
|
|
(7) |
|||
|
|
|
|
|
|
|
n2 |
|
|
|
|||||||
|
|
|
|
|
|
m2 |
|
|
|
p2 |
|
|
|
|
|||
Умова перетину двох непаралельних прямих у просторi: |
|
||||||||||||||||
|
|
|
m1 |
n1 |
|
|
p1 |
= 0. |
(8) |
||||||||
|
|
x2 − x1 y2 |
− y1 |
|
z2 − z1 |
|
|
||||||||||
|
|
m |
2 |
|
|
n |
2 |
|
|
p |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тепер розглянемо взаємне розмiщення прямої та площини. Нехай площина задається загальним рiвнянням Ax + By + Cz + D = 0, а пряма
– канонiчним рiвнянням |
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
m |
|
n |
|
p |
|
|
38 |
|
|
|
|
|

Синус кута ϕ мiж прямою та площиною знаходять за формулою:
sin ϕ = |
√ |
|
|
|Am + Bn + Cp| |
. |
(9) |
|||||
|
|
|
|
|
|
|
|
||||
|
A2 + B2 + C2 |
|
m2 + n2 + p2 |
|
|
||||||
Умова паралельностi прямої та |
площини: |
|
|
||||||||
|
p |
|
|
||||||||
|
|
Am + Bn + Cp = 0. |
|
(10) |
|||||||
Умова перпендикулярностi прямої та площини: |
|
|
|||||||||
|
|
|
A |
= |
B |
= |
C |
. |
|
(11) |
|
|
|
|
|
n |
|
|
|||||
|
|
m |
|
|
p |
|
|
||||
Якщо AM + Bn + Cp 6= 0, то пряма перетинає площину. Якщо
AM + Bn + Cp = 0 i Ax0 + By0 + Cz0 + D 6= 0, то пряма паралельна площинi. Якщо AM + Bn + Cp = 0 i Ax0 + By0 + Cz0 + D = 0, то пряма лежить у площинi.
|
5x + 4y − z − 7 = 0 |
записати в |
Приклад 1. Рiвняння прямої |
2x − y + 3z − 1 = 0 |
канонiчному виглядi.
Розв’язання. З рiвнянь площини, що утворюють пряму, випишемо координати нормальних векторiв ~n1 = {2; −1; 3}, ~n2 = {5; 4; −1}. Знайдемо
|
|
~ |
|
|
|
|
|
напрямний вектор прямої S = {m, n, p}, вiн має бути перпендикулярним |
|||||||
|
|
|
|
~ |
можемо прийняти векторний добуток |
||
до векторiв ~n1 та ~n2. Тому за S |
|||||||
векторiв ~n1 та ~n2: |
|
= |
|
|
|
= 11~i + 17~j + 13~k. |
|
S~ = ~n1 ~n2 |
~ |
~ |
~ |
||||
2 1 3 |
|||||||
|
× |
|
i |
j |
k |
|
− |
|
|
− |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
5 |
4 |
|
|
|
|
|
|
|
|
|
|
|
¨
Тепер необхiдно знайти точку M, яка лежить на прямiй. Iї координати мають задовольняти систему
2x − y + 3z − 1 = 0 5x + 4y − z − 7 = 0.
Покладемо x = 0, тодi
−y + 3z − 1 = 0 4y − z − 7 = 0.
Розв’язавши останню систему, одержимо, що y = 2, z = 1. Тому рiвняння прямої в канонiчному виглядi запишеться так:
x |
= |
y − 2 |
= |
z − 1 |
. |
−11 |
|
|
|||
17 |
13 |
|
|||
39
Приклад 2. Знайти кут ϕ мiж прямою, що проходить через точки
A(5; 1; −4) i B(6; 1; −3) та площиною 2x − 2y + z − 3 = 0.
Розв’язання. За напрямний вектор прямої можна взяти вектор
~ ~ |
−2; 1}. |
S=AB={1; 0; 1}, а за нормальний вектор площини – вектор ~n = {2; |
|
Тодi за формулою (9) |
|
|
sin ϕ = |
|
|
|
|
|1 · 2 + (−2) · 0 + 1 · 1| |
|
= |
|
|
3 |
|
= |
1 |
|
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
√12 + 02 + 12p22 + (−2)2 + 12 |
|
3√2 |
√2 |
|||||||||||||||||||
|
|
1 |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
звiдки ϕ = arcsin √ |
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Аудиторнi завдання |
|
|
|
|
|
|
|
|
|
|||||||
1. |
Записати рiвняння прямої, що проходить через точку M(3; −1; 2) |
|||||||||||||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
паралельно вектору AB, якщо A(−1; 2; 3), B(2; −3; 1). |
|
|
|
|||||||||||||||||||||
2. |
Записати рiвняння прямої, що проходить через точку M(2; 0; −3) |
|||||||||||||||||||||||
паралельно прямiй |
2x + y + 3z − 11 = 0, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
5x + 4y + z + 8 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3. |
Знайти точку перетину прямої та площини |
|
|
|
|
|
|
|
|
|||||||||||||||
|
x − 7 |
= |
y − 4 |
= |
z − 5 |
, 3x |
− |
y + 2z |
− |
5 = 0. |
|
|
|
|||||||||||
|
5 |
|
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2y + 3 = 0 |
|
|
|
|
|
|
|
|
|
|||
4. |
Знайти кут мiж прямою 3y−+ z − 1 = 0 |
та площиною |
||||||||||||||||||||||
2x + 3y − z + 1 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
Знайти параметричне рiвняння прямої, що проходить через точки |
|||||||||||||||||||||||
M(2; −5; 1) та N(−1; 1; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Домашнi завдання
1. Записати рiвняння площини, що проходить через пряму
x − 2 |
= |
y − 3 |
= |
z + 1 |
5 |
|
|
||
1 |
2 |
|||
перпендикулярно до площини x + 4y − 3z + 7 = 0. 2. Обчислити вiдстань мiж прямими
x − 2 |
= |
y + 1 |
= |
z |
та |
x − 7 |
= |
y − 1 |
= |
z − 3 |
. |
3 |
|
|
3 |
|
|
||||||
4 |
2 |
|
4 |
2 |
|
||||||
40
