Рудницький В.Б._ Вища матем в правах и задачах

§3. Метод Крамера. Матричний метод розв’язування систем лiнiйних алгебраїчних рiвнянь

Розглянемо систему лiнiйних алгебраїчних рiвнянь

a11x1 + a12x2 + . . . + a1nxn = b1,

a21x1 + a22x2 + . . . + a2nxn = b2, (1)

. . . . . . . . . . . . . . . . . . . . . . .

an1x1 + an2x2 + . . . + annxn = bn.

Якщо визначник системи det A 6= 0, то справедливi формули Крамера для обчислення невiдомих xi:

Приклад 1. Методом Крамера розв’язати систему лiнiйних алгебра-

2x1 − x2 − 3x3 = 3 3x1 + 4x2 − 5x3 = −8

2x2 + 7x3 = 17.

Розв’язання. Так як визначник даної системи

то дану систему можна розв’язати за формулами Крамера. Знаходимо

Використовуючи операцiю множення матриць, систему (1) можна

11

A−1AX = A−1B, звiдки видно, що X = A−1B.

Приклад 2. Матричним методом розв’язати систему рiвнянь

−

Аудиторнi завдання

Розв’язати ситему: а) за формулами Крамера; б) матричним методом.

Розв’язати ситему: а) за формулами Крамера; б) матричним методом.

12

7.5x2 + 4x3 = −20 8. 4x1 + x2 + 4x3 = 6

§4. Ранг матрицi. Теорема Кронекера–Капеллi. Метод Гаусса

Тут A – матриця коефiцiєнтiв при невiдомих, X – стовпчик невiдомих, B

– стовпчик вiльних членiв. Поряд з матрицею A розглядають розширену матрицю системи:

13

Максимальний порядок вiдмiнних вiд нуля мiнорiв матрицi A називається її рангом. Ранг матрицi можна знайти методом елементарних перетворень. Задану матрицю елементарними перетвореннями рядкiв i стовпцiв зводять до схiдчастої. Кiлькiсть ненульових рядкiв схiдчастої матрицi дорiвнює рангу матрицi.

Приклад 1. Елементарними перетвореннями знайти ранг матрицi.

При цьому виконали такi елементарнi перетворення:

1)до другого рядка додали перший, помножений на (−2); до третього – перший, помножений на (−3), до четвертого – перший, помножений на (−1);

2)до третього рядка додали другий, помножений на (−1), i помiняли мiсцями третiй i четвертий рядки. Отримали, що rang A = 3.

Система рiвнянь (1) називається сумiсною, якщо вона має хоча б один розв’язок i несумiсною, якщо вона не має жодного розв’язку.

Теорема Кронекера–Капеллi. Для того, щоб лiнiйна система (1) була сумiсною, необхiдно i досить, щоб ранг розширеної матрицi цiєї системи дорiвнював рангу її основної матрицi, тобто

rang A = rang A.

14

Приклад 2. Перевiрити чи сумiсна система

x1 + 5x2 − x3 = 3,

2x1 + 4x2 − 3x3 = 2,3x1 − x2 − 3x3 = −7.

Розв’язання. Знайдемо ранг розширеної матрицi за допомогою елементарних перетворень

З останньої матрицi маємо, що rang A = rang A = 3. Отже, згiдно теореми Кронекера–Капеллi дана система сумiсна.

Теорема Кронекера–Капеллi дає необхiднi i достатнi умови сумiсностi лiнiйної системи, але не дає способу знаходження розв’язку цiєї системи.

Розглянемо систему лiнiйних рiвнянь, у якiй m = n. Ефективним методом розв’язування таких систем є метод Гаусса. Вiн полягає у послiдовному виключеннi невiдомих. Елементарними перетвореннями систему лiнiйних рiвнянь (1) приводимо до схiдчастої:

З останньої системи послiдовно знаходимо xn, xn−1, . . . , x1.

На практицi зручнiше приводити до схiдчаcтого вигляду не саму систему, а розширену матрицю, яка їй вiдповiдає.

Приклад 3. Методом Гаусса розв’язати систему

x1 + x2 + 2x3 = 6, x1 − 2x2 − 3x3 = −3,

2x1 + x2 − x3 = −1.

Розв’язання. До схiдчатого вигляду приводимо розширену матрицю системи

15

З останньої матрицi послiдовно знаходимо: x3 = 3, x2 = −2, x1 = 2.

Система називається однорiдною, якщо всi її вiльнi члени b1, b2, . . . , bn рiвнi нулю. В уciх iнших випадках система неоднорiдна.

Однорiдна система завжди сумiсна, бо вона володiє так званим тривiальним (або нульовим) розв’язком x1=x2= . . . =xn=0. Вiдповiдь на питання, при яких умовах однорiдна система має нетривiальний розв’язок, дає наступна теорема.

Теорема. Квадратна однорiдна система має нетривiальний розв’я- зок тодi i лише тодi, коли визначник, складений iз коефiцiєнтiв при невiдомих, дорiвнює нулю.

Однорiдну систему можна розв’язати методом Гаусса. Для цього потрiбно взяти тi рiвняння системи, якi мiстять вiдмiнний вiд нуля мiнор, прийнявши всi iншi доданки за вiльнi члени. Тодi отримаємо множину розв’язкiв даної системи.

Приклад 4. Розв’язати однорiдну систему

З останньої системи знаходимо: x2 = C, x1 = −2C.

Таким чином, дана система має безлiч розв’язкiв, якi визначаються спiввiдношеннями x1 = −2C, x2 = C, x3 = C, де C – довiльна стала.

16

17

§5. Вектори та лiнiйнi операцiї над ними. Скалярний добуток двох векторiв

Вектором будемо називати напрямлений вiдрiзок. Довжину вiдрiзка, який зображає вектор, називають модулем або довжиною вектора. Якщо модуль вектора дорiвнює нулю, то вектор буде нульовим i напрям його невизначений.

Вектори, якi лежать на однiй прямiй або на паралельних прямих, називаються колiнеарними. Вектори, що лежать в однiй площинi або в паралельних площинах, називаються компланарними. Якщо вектори спiвнапрямленi i мають однаковi модулi, то такi вектори називаються рiвними. Якщо вектори мають однаковi модулi але протилежнi напрямки, то їх називають протилежними.

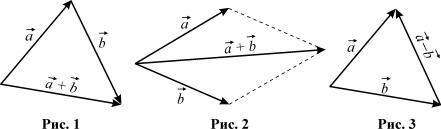
Сумою двох векторiв, розмiщених послiдовно (тобто кiнець першого вектора є початком другого), називають вектор, який сполучає початок першого вектора з кiнцем другого (рис.1). Це правило додавання векторiв називають правилом трикутника. Якщо ж два вектори мають спiльний початок, то для знаходження суми таких двох векторiв необхiдно побудувати на них паралелограм (рис.2). Вектор, який збiгається з дiагоналлю побудованого паралелограма, що має спiльний початок iз заданими векторами, буде сумою цих векторiв. Це правило додавання двох неколiнеарних векторiв називають правилом паралелограма.

який треба додати до вектора b, щоб дiстати вектор ~a, отже, ~a − b = ~c,

~

якщо b + ~c = ~a (рис.3). Неважко зрозумiти, що для того, щоб вiд вектора

18

напрямлений з ним при λ > 0 та протилежно напрямлений при λ < 0.

Лiнiйною комбiнацiєю векторiв ~a1,

~a2, . . . ,~an називається вектор

λ1~a1 + λ2~a2 + · · · + λn~an,

де λ1, λ2, . . . , λn – дiйснi числа.

Одиничним вектором (ортом) називають вектор, довжина якого дорiвнює одиницi i який спiвнапрямлений з даним вектором. Щоб знайти орт заданого вектора, потрiбно помножити вектор на число, обернене до модуля даного вектора.

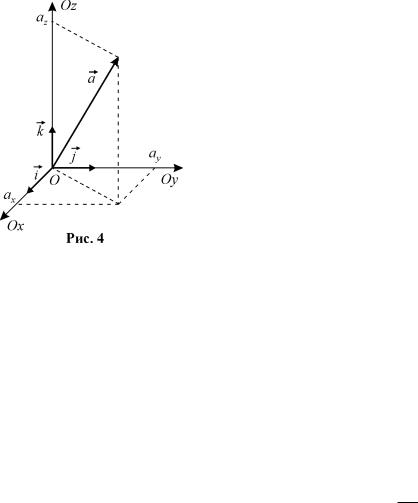
Якщо маємо вектор у системi координат, то це означає, що задано його координати, тобто алгебраїчнi проек-

цiї вектора на вiдповiднi осi координат. Нехай маємо прямокутну декартову систему координат у просторi (рис.4). Координати вектора позначимо через x, y, z. Тодi будемо записувати ~a = {x, y, z}. Очевидно, що

Якщо маємо двi точки A(x1, y1, z1) та B(x2, y2, z2), то вектор AB має координати

19

Якщо задано вектори ~a1 = {x1, y1, z1}, ~a2 = {x2, y2, z2}, то в координатнiй формi

~c = λ~a1 = {λx1, λy1, λz1}.

Якщо вектори колiнеарнi, то їх координати пропорцiйнi. Усе вищеска-

~

де ϕ – кут мiж векторами ~a та b.

Скалярний добуток (a,~) називають скалярним квадратом вектора ~a. Вiн дорiвнює квадрату модуля вектора ~a, тобто (a,~) = ~a 2 = |~a|2. Якщо вектори задано сво¨ıми декартовими координатами, тобто ~a = {x1, y1, z1},

Очевидно, що

Розв’язання. Якщо два вектора перпендикулярнi, то косинус кута мiж ними дорiвнює нулю. Тому параметр α будемо шукати з умови, що

20