Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Херсонский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Рудницький В.Б._ Вища матем в правах и задачах

.pdf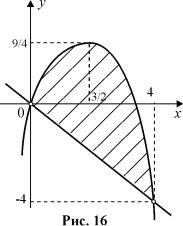

Скачиваний:

Добавлен:

07.02.2016

Размер:

703.72 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

§15. Обчислення площi плоскої фiгури

Площу криволiнiйної трапецiї, обмеженої кривою y = f(x) (f(x) ≥ 0), прямими x = a, x = b i вiдрiзком [a, b], обчислюємо за формулою:

S = f(x) dx.

Якщо крива задана параметрично x=x(t), y=y(t), то площу криволiнiйної трапецiї, обмеженою цiєю кривою, прямими x = a, x = b i вiдрiзком [a, b] осi Ox обчислюємо за формулою:

S = y(t) x0(t) dt,

де t1 i t2 визначаються iз рiвнянь a = x(t1), b = x(t2).

Площа криволiнiйного сектора, обмеженого кривою, заданою в полярнiй системi координат рiвнянням ρ = ρ(θ) i двома полярними радiусами θ = α, θ = β (α < β), обчислюється за формулою:

S =

Zα

ρ2dθ.

Приклад. Обчислити площу фi-

гури, обмеженої лiнiями y = 3x − x2 i

y = −x.

Розв’язання. Знаходимо точки пе-

ретину кривих i будуємо фiгуру.

y = 3x − x2

−x = 3x − x2

y = −x

y = −x.

Одержимо:

x1 = 0, x2 = 4; y1 = 0, y2 = −4. Тодi

S = 4(3x

(

x))dx =

(4x

x2)dx = 2x2

−

101

			Аудиторнi завдання
Обчислити площу фiгури, обмеженої лiнiями:
1. y2 = 9x, y = 3x;							2. y=x2+4x, y = x+4;
	x = a(t − sin t),							−
3.	y = a(1 − cos t), вiссю Ox (1-ї арки); 4. ρ = a(1								cos ϕ);
5. y = x2, y = x + 2							6. xy = 2, x+2y=5.
			Домашнi завдання
Обчислити площу фiгури, обмеженої лiнiями:
					16
1.	y = −x2, x + y + 2 = 0;			2.	y=		, y=17−x2; (I-а четверть)
1.	y = −x2, x + y + 2 = 0;			2.	y=	x2	, y=17−x2; (I-а четверть)
3.	y = sin x, y = cos x; x = 0;			4.	y = x2 − 4, x − y + 8 = 0;
	x = a cos3 t,
5.	y = a sin3 t ;			6.	ρ = a sin 3θ;
7. y = √			, xy = 1; x = 8, y = 0;
7. y = √		x	, xy = 1; x = 8, y = 0;

Самостiйна робота

Обчислити (з точнiстю до двох знакiв пiсля коми) площу фiгури, обме-

женої лiнiями:
1.	ρ = 3√			;	2.	y = x2, y = 3 − x;
			cos 2ϕ
3.	y = √x, y = x3;				4.	y = 7 sin3 t				;
							7 cos3 t,
5.	ρ = 3 cos 2ϕ;				6.	y2 = 9x, y = 3x;
7.	ρ = 2(1 − cos ϕ);				8.	y = 2 sin t;
							x = 3 cos t,
9.	y = x2, y = 2 − x2;				10.		ρ = 3 sin 4ϕ;
11.		y = x3, y = 1, x = 0;			12.		y = x + 1, y = cos x, y = 0;
13.		ρ2 = 2 sin 2ϕ;			14.		x = 4(t − sin t),
							y = 4(1 − cos t);
							1			x2
15.		ρ = 2 + cos ϕ;			16.		y =		,	y =		;
								1 + x2			2
17.		y2 = x+1, y2 = 9−x;			18.		y2 = x3, x = 0, y = 4;
19.		ρ = sin2 ϕ;			20.		y = 2x, y = 2x − x2, x = 0, x = 2.

102

§16. Подвiйний iнтеграл

Подвiйний iнтеграл, згiдно означення рiвний

f(x, y) dxdy =

= lim f(ξi, ηi)ΔSi,

d→0

i=1

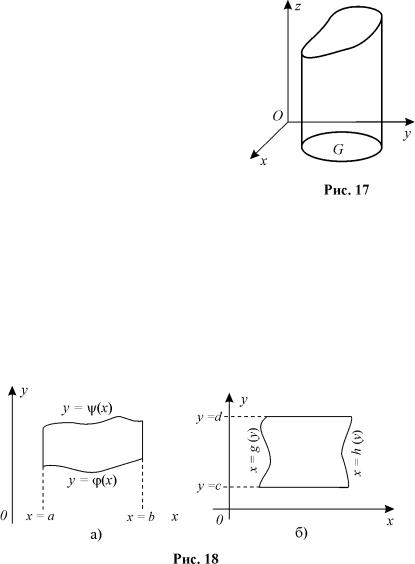
представляє собою об’єм прямого цилiндричного тiла, побудованого на областi G як на основi i обмеженого зверху поверхнею z=f(x, y).

Якщо f(x, y) ≡ 1, то dxdy

чисельно рiвний площi областi G (рис.17).

Обчислення подвiйного iнтеграла зводиться до повторного iнтегрування за схемою:

а) Нехай G – область обмежена прямими x = a, x = b i кривими y = ϕ(x) i y = ψ(x) (рис. 18а)), тодi

ZZ	b		ψ(x)
ZZ	f(x, y) dxdy = Z	dx	Z	f(x, y) dy.
G	a	ϕ(x)

б) Якщо область G обмежена прямими y = c, y = d i кривими x = g(y),

103

x = h(y) (рис. 18б)), то подвiйний iнтеграл обчислюється за формулою

ZZ	d	h(y)
ZZ	f(x, y) dxdy = Z	dy Z	f(x, y) dy.
G	c	g(y)

В обох випадках внутрiшнiй iнтеграл обчислюється при умовi, що одна змiна константа: так у випадку а) x = const у випадку б) y = const.

Аудиторнi завдання

1. Змiнити порядок iнтегрування в iнтегралах, область iнтегрування зобразити на рисунку

	√			3	y+3
1 3−x		25−x	2
	4			2

а) Z0	dxZ2	f(x, y) dy	б) Z0	dx	3Z	f(x, y) dy в) Z0	dy Z2	f(x, y) dx
	2x				4 x		2y

2. Визначити об’єм тiла, обмеженого вказаними поверхнями. Тiло i область iнтегрування зобразити на рисунку

а) z = 0, z = 2x, x + y = 3, x = r

;

= 0

x + y = 2

y = √

−

;

б) x = 0, y = 0, z 2

в) z = 0, z = 1 − x

, y = 0, y = 3 − x.

Домашня робота

1. Змiнити порядок iнтегрування в iнтегралах, область iнтегрування зобразити на рисунку

0	x+3		0		45 y	1	x2+1
а) Z	dxZ2	f(x, y) dy	б) Z	dy	Z	f(x, y) dx в) Z	dx Z	f(x, y) dy
−1 2x			−4 −√		9+y2	0	−1

2. Визначити об’єм тiла, обмеженого вказаними поверхнями. Тiло i область iнтегрування зобразити на рисунку

а) z = 0, z = 1 − y, y = x2;

б) z = 0, z = 2 − x, x = 1, x = y2;

в) x = 0, y = 0, z = 0, x + y = 1, z = x2 + 3y2.

104

un, де un R називається

Самостiйна робота

Змiнити порядок iнтегрування в iнтегралах, область iнтегрування

зобразити на рисунку

√

−

25−y2

dy Z2

f(x, y) dx

4 y

3−x

√

9+y2

dx Z2

f(x, y) dy

f(x, y) dx

−2

4 y

2. Визначити об’єм тiла, обмеженого вказаними поверхнями. Тiло i

область iнтегрування зобразити на рисунку

а) x = 0, y = 0, z = 0, x = 1, x + y = 2, z = x2 + 12 y2; б) x = 0, y = 0, z = 0, y + z = 1, x = y2 + 1;

в) z = 0, z = 1 − y2, x = y2, x = 2y2 + 1; г) z = 0, z = √1 − y, y = x2.

§17. Числовi ряди. Ознаки збiжностi числових рядiв

∞

Сума виду u1 + u2 + . . . + un + . . . =

n=1

числовим рядом, доданки un – членами ряду.

Сума Sn = u1 +u2 +. . .+un називається n-ою частинною сумою ряду.

Якщо послiдовнiсть частинних сум {Sn} збiжна i lim Sn = S, то число S

n→∞

називається сумою ряду, а сам ряд – збiжним. Якщо послiдовнiсть {Sn} скiнченної границi не має, то ряд називається розбiжним.

Ряд a + aq + aq2 + . . . + aqn + . . . представляє собою суму членiв геометричної прогресiї iз знаменником q. При |q| < 1 цей ряд збiгається i

його сумою є число S = a/(1 − q); при |q| ≥ 1 даний ряд розбiгається.

∞

Ряд 1+ 12 +. . . n1 +. . . = X n1 називається гармонiйним, вiн розбiжний.

n=1

∞

X 1

Ряд n=1 nα називається узагальненим гармонiйним рядом. При α>1 вiн збiгається, при α ≤ 1 – розбiгається.

105

= 13 6= 0,

Ознаки збiжностi рядiв з додатними членами

1. Необхiдна ознака збiжностi ряду.
Якщо числовий ряд збiгається, то lim un = 0.
n→∞
2. Ознаки порiвняння:
Нехай є два ряди	∞
	∞
u1 + u2 + . . . + un + . . . =	X	(1)
u1 + u2 + . . . + un + . . . =	un	(1)
та	n=1
та	∞
	∞
v1 + v2 + . . . + vn + . . . =	X	(2)
v1 + v2 + . . . + vn + . . . =	vn,	(2)

n=1

причому для всiх n ≥ n0 виконується умова 0 < un ≤ vn. Тодi

а) якщо збiгається ряд (2), то збiгається i ряд (1); якщо розбiгається ряд (1), то i розбiгається ряд (2).

б) якщо iснує скiнченна вiдмiнна вiд нуля границя lim (un/vn) = k,

n→∞

то ряди (1) та (2) одночасно збiгаються або розбiгаються. 3. Ознака Даламбера.

Якщо для ряду (1) iснує lim un+1 = `, то ряд збiгається при ` < 1 та

n→∞ un

розбiгається при ` > 1. При ` = 1 ознака Даламбера не дає вiдповiдi на питання про збiжнiсть ряду.

4. Ознака Кошi.

√

Якщо для ряду (1) iснує границя lim n un = `, то при l < 1 ряд збi-

n→∞

гається; при ` > 1 – розбiгається. При ` = 1 ознака Кошi не дає вiдповiдi на питання про збiжнiсть ряду.

5. Iнтегральна ознака Кошi.

Нехай члени ряду (1) монотонно спадають i функцiя y = f(x) неперервна при x ≥ 1, така, що f(n) = un. Тодi ряд (1) збiгається чи розбiгається

∞

в залежностi вiд того, збiгається чи розбiгається iнтеграл Z1

f(x)dx.

Приклад. Дослiдити на збiжнiсть числовi ряди:

∞

∞ 1

∞

n + 1

а) n=1

;

б) n=1

;

в) n=1

−

5n + 1

−

Розв’язання. а) перевiримо необхiдну ознаку збiжностi ряду. Загаль-

ний член ряду un = 3n − 1 , тому

lim un = lim

n→∞ n→∞ 3n − 1

106

тобто ряд розбiжний.

б) застосуємо ознаку порiвняння. Порiвняємо даний ряд з гармонiйним:

	1						1
k = lim		5n + 1	=	lim	n	=		.
		1/n
n→∞				n→∞ 5n + 1 5

Оскiльки границя iснує i не дорiвнює нулю, то заданий ряд розбiжний, бо розбiжним є гармонiйний ряд.

в) використаємо ознаку Кошi:

n + 1

nlim

= nlim

< 1,

−

→∞

тому ряд збiгається.

Аудиторнi завдання

Дослiдити на збiжнiсть числовi ряди:

∞

;

sin

;

n=1

2n3

−

n=1

∞

;

∞

;

n=1

ln(n + 1)

2n(n + 2)

n=1

∞

n tg

;

∞

;

n=1

2n+1

n=1

1 + n

∞

7. n=2

;

8. n=1

;

n ln2 n

1 + n2

1 n + 2

+2n

∞ e−√n

∞

√

;

10.

n=1

;

n + 1

n=1

11.

∞

;

12.

∞

n=1 2n + 1

n=1 lnn

(n + 1) .

Домашнi завдання

Дослiдити на збiжнiсть числовi ряди:

∞ 1

√

∞

;

1. n=1 n

( n+1− n−1);

2. n=1 n√n + 1

∞

n + 1

∞

;

n=1

2n + 5

3nn!

n=1

107

n=1

∞

11. arctgn

n=1

∞

n=1

∞

	∞	n
5.	X		;
5.	n=1	(n + 1)!	;
7.	n=1	2n − 1 ;
7.	∞	2n − 1 ;
	X
	n=1	n!
	n=1
	∞			π
9.	X(3n − 1) sin				;
9.	X(3n − 1) sin			4n	;

n1 ;

13.arctg n;

15. n=1 (4n−1)(4n+5) .

∞

4n arcsin

;

n=1

∞

;

−

1)!

n=1

10.

∞

;

n=1 5n

n + 3

12.

∞

n=1 sin n3

;

∞

14.

;

n=1

n ln7 n

Самостiйна робота

Дослiдити на збiжнiсть числовi ряди:

∞

n n + 2)!

∞

1. n=1

(

;

2. n=1

;

∞

;

∞

n=1(2n + 1) tg

n=1

10 n7;

∞

n2 + 3

;

n=1

5n(n + 3)!

n=1

(n + 1)!

∞

(n + 1)n

∞

3n − 1

;

√

;

n=1

n7n

∞

(2n − 1)3

;

10. ∞

;

(2n)!

n=1

n=1 4n!

11.

∞

10n

;

12.

∞

5n − 1

;

n=1

∞

n2 + 5n + 8

13.

arctg

;

14.

;

n=1

2n + 1

n=1

3n2

−

15.

∞

;

16.

∞

3n2 + 4n + 5

;

n=1

(ln(n + 1))2n

n=1

6n2

−

n + 1

−n

17.

∞

;

18.

∞

;

n=1

tg 2n + 1

108

∞

10n

19.

;

n=1

(ln(n + 2))n

∞

21.

;

n=1

;

23.

∞

7 + n

n=1

49 + n2

∞

25.

;

n=1

(n + 5) ln(n + 5)

ln(3n + 2)

∞

27.

;

∞

n + 2p

n=1

(3n + 2)

3 ln(3n + 2)

29.

;

n=1

n2 + 6n + 9

∞

n + 2

31.

n√3

;

n=1

∞

33.

√

n=1

n3 + 3n

∞

n + 3

20.

arcsin

;

n=1

2n + 5

∞

22.

;

n=1

(3 + 2n) ln5(3 + 2n)

∞

24.

;

n=1

4 (4n + 5)3

∞

ln(n + 4)

26.

;

n=1

(n + 4) ln2(n + 4)

∞

(n + 1)(n + 4)

28.

;

n=1

∞

30.

(3n

−

2)(7n

−

1) ;

n=1

∞

32.

;

3n2

−

n + 1

n=1

§18. Знакозмiннi ряди. Ознака Лейбнiца

Ряд виду
u1 − u2 + u3 − . . . + (−1)n−1un + . . . ,	(1)

де un > 0, називається знакозмiнним рядом. Цей ряд можна дослiдити на збiжнiсть за допомогою ознаки Лейбнiца.

Ознака Лейбнiца. Ряд (1) збiжний, якщо: 1) un+1 < un, (n = 1, 2, . . .);

2) lim un = 0.

n→∞

Якщо ряд, складений з абсолютних величин, тобто ряд

|u1| + |u2| + . . . + |un| + . . .

збiгається, то ряд (1) називається абсолютно збiжним . Якщо ряд з абсолютних величин розбiгається, але ряд (1) збiгається за ознакою

Лейбнiца, то такий ряд називається умовно збiжним.

∞

Приклад. Дослiдити на збiжнiсть знакозмiнний ряд P (−1)n lnnn.

n=1

109

Розв’язання. Використаємо ознаку Лейбнiца

|u1|

ln 1

= 0;

u2 =

ln 2

> |u3| =

ln 3

> . . .

n→∞

−

n→∞

n→∞ n

n→∞ 1

lim

(

1)n ln n

lim

ln n =

lim n =

lim

1 = 0.

За ознакою Лейбнiца ряд збiгається. Перевiримо його на абсолютну

∞

збiжнiсть. Розглянемо ряд з абсолютних величин X lnnn. Дослiдимо

n=1

його на збiжнiсть за допомогою iнтегральної ознаки Кошi. Маємо

ln x

∞

ln x

∞

dx = Z1

lim

ln xd(ln x) =

f(x) =

;

ln xd(ln x) =

N→∞ Z1

= lim

ln2 x

lim

ln2 N

−

ln2 1

= lim

ln2 N

∞

N→∞

Таким чином, ряд з абсолютних величин розбiгається. Тому початковий ряд умовно збiжний.

Аудиторнi завдання

Дослiдити на умовну та абсолютну збiжнiсть ряди:

∞

(−1)n−1 √

;

(−1)n−1n2−n;

n=1

∞

cos(2nα)

(−1)n−1

6n + 5

;

+ 1

;

n=1

∞

(−1)n

n ln2 n

;

(−1)n

n=2

n=1

Домашнi завдання

Дослiдити на умовну та абсолютну збiжнiсть ряди:

∞

( 1)n+1

∞

( 1)n−1

−

(2n

1)3

;

ln(n + 1)

;

n=1

∞

(

1)n

∞

(−1)n+1

−

2n + 1

;

4. n=1 n ln n ;

3. n=1

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.07.2025270.85 Кб0Розділ_9_10.doc
#
01.05.2025216.58 Кб0розмноження.doc
#
10.09.2019153.6 Кб2РОЗРОБКА СТРАТЕГІЇ МАРКЕТИНГУ.doc
#
01.05.20251.22 Mб0РОЛЬ СТВОЛА МОЗГА И МОЗЖЕЧКА В РЕГУЛЯЦИИ ПОЗЫ И...doc
#
01.04.2025122.07 Mб0РТС. Конспект лекцій.doc
#
07.02.2016703.72 Кб82Рудницький В.Б._ Вища матем в правах и задачах.pdf
#
23.08.2019260.1 Кб2Рук1.doc
#
17.08.2019101.15 Кб10с пылью и сором.docx
#
01.05.2025580.1 Кб0С.. Zapiska_DP1 (2).doc
#
04.11.2018272.38 Кб4Сам раб БМ 1.doc
#
13.11.2018584.7 Кб9Сам робота ділова нова.doc