Практика:

1. Скласти двоїсту задачу та визначити методи її розв’язання.

min Z=5X1 + Х2

при X1 + Х2 12

4Х1 + Х2  4

X1,X2 0

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений.Рассмотрим целевую функцию задачи F = 5x₁+x₂ → min. Построим прямую, отвечающую значению функции F = 0: F = 5x₁+x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (5; 1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией. Область допустимых решений представляет собой линию.Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых: x₁+x₂=12 x₁=0 Решив систему уравнений, получим: x₁ = 0, x₂ = 12 Откуда найдем минимальное значение целевой функции: F(X) = 5*0 + 1*12 = 12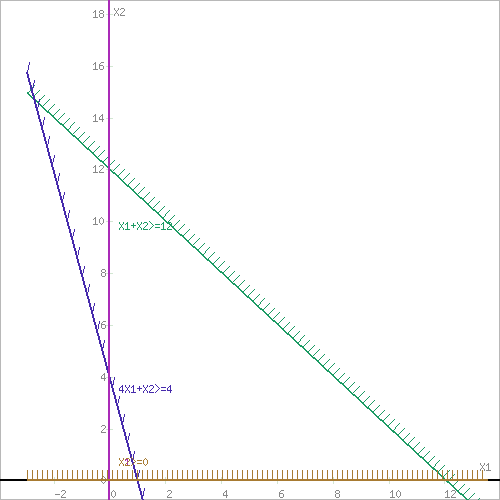

2. На трьох складах оптової бази зосереджений однорідний вантаж у кількостях 180,65 і 85 од. Цей вантаж необхідно перевезти в чотири магазини. Кожний з магазинів повинен одержати відповідно 130,40,60 і 30 од. вантажу. Тарифи перевезень зазначені в таблиці:

Склади	Магазини
		1	2	3	4
	1 2 3	2 7 2	3 3 1	4 1 4	3 2 6

Скласти опорний план перевезень.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

	1	2	3	4	Запасы
1	2	3	4	3	180
2	7	3	1	2	65
3	2	1	4	6	85
Потребности	130	40	60	30

Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 180 + 65 + 85 = 330 ∑b = 130 + 40 + 60 + 30 = 260 Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 70 (330—260). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю. Занесем исходные данные в распределительную таблицу.

	1	2	3	4	5	Запасы
1	2	3	4	3	0	180
2	7	3	1	2	0	65
3	2	1	4	6	0	85
Потребности	130	40	60	30	70

Минимальные затраты составят: F(x) = 2*130 + 3*25 + 0*25 + 1*60 + 2*5 + 1*40 + 0*45 = 445 Анализ оптимального плана. Из 1-го склада необходимо груз направить в 1-й магазин (130), в 4-й магазин (25) Из 2-го склада необходимо груз направить в 3-й магазин (60), в 4-й магазин (5) Из 3-го склада необходимо весь груз направить в 2-й магазин На 1-ом складе остался невостребованным груз в количестве 25 ед. Оптимальный план является вырожденным, так как базисная переменная x₁₅=0. На 3-ом складе остался невостребованным груз в количестве 45 ед. Оптимальный план является вырожденным, так как базисная переменная x₃₅=0.