Метод найменших квадратів

Нехай – послідовність значень незалежної змінної, а– послідовність відповідних значень залежної змінної.Припустимо, що точки ,, ...,приблизно розташовуються на одній прямій. Поставимо за мету підібрати рівняння прямої , яка є найточнішим наближенням залежності міжта.

Зміст методу найменших квадратів полягає у тому, що шукану лінію підбирають таким чином, щоб сума квадратів відхилень була б найменшою. Маємо

.

Використовуючи необхідну умову екстремуму функції , отримаємо:

.

Тобто коефіцієнти іпрямоїобчислюються із системи рівнянь:

Приклади розв’язання типових завдань

Приклад 1. Знайти похідну функції у точціМ(3;2;1) за напрямом вектора , деN(5;4;2). Знайти градієнт функції у точці М.

Розв’язання.

Знайдемо вектор та його направляючі косинуси:

Обчислимо значення частинних похідних в точці М:

;

Отже, .

.

Приклад 2. Знайти умовний екстремум функції u= f(x, y) = відносно рівняння зв’язку.

Розв’язання. Функції f і φ подвійно неперервно диференційовні. Матриця Якобі в даному випадку має вигляд (2х-2y), і її ранг дорівнює 1 в усіх точках, що задовольняють рівняння зв’язку. Отже, можна скористатися методом Лагранжа. Запишемо функцію Лагранжа

.

Згідно з необхідними умовами дістанемо систему:

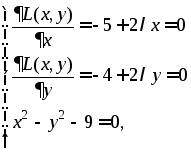
з якої знаходимо х=–5, у=4 при λ=1/2. Таким чином, функція f може мати умовний екстремум тільки в двох точках (–5; 4) і (5;–4).

Обчислимо другий диференціал функції Лагранжа: , тоді.

Знайдемо перший диференціал функції φ (х,y).

У точках (–5; 4) і (5; – 4) диференціали dx і dy пов’язані рівністю: 5dx +4dy =0, dy= При виконанні цієї умови другий диференціал функції Лагранжа в точці (–5; 4) є додатньо-визначеною квадратичною формою , а в точці (5; –4) — від’ємно визначеною формою. Отже, функціяf у точці (–5; 4) має умовний мінімум  u(-5,4)=15, а в точці (5;-4) — умовний максимум u(5;-4)=-3.

Приклад 3. Експериментально одержані значення функціїу п’яти точках, які записані у таблиці:

	1	2	3	4	5
	3,9	4,1	3,5	2,5	2,4

Методом найменших квадратів знайти функцію , що виражає приблизно функцію. Зробити рисунок, на якому побудувати графік функціїта експериментальні точки.

Розв’язання. Для знаходження коефіцієнтів іобчислимота, результати занесемо у таблицю:

	1	1	3,9	3,9
	2	4	4,1	8,2
	3	9	3,5	10,5
	4	16	2,5	10
	5	25	2,4	12
	15	55	16,4	44,6

Маємо:

.

Отже,

.

Пряма та експериментальні точки показані на рис. 4.

Самостійна (домашня) робота:

6. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах, ч.1..-М.:Высшая школа, 1967.-297с. Стор.

7. Бардачов Ю.М. Практикум з вищої математики. Ч. 1. / Ю.М. Бардачов, В.В, Крючковський, О.В. Цибуленко, А.М, Матвієнко, І.В. Вигоднер. — Херсон: "ОЛДІ-плюс", 2010. — 390 с. Розділ

8. Шипачев В.С. Задачник по высшей математике:учеб.пособие для вузов.–М.:Высш.шк., 2000.–304с. №

9. Рудницький В.Б., Гpипинська H.В., Кучерук О.Я., Моpоз В.В. Вища математика у вправах i задачах: Hавчальний посiбник для студентів економiчних та технологiчних спецiальностей вузiв. – Хмельницький: ТУП, 2004. – 130 с. – С.56-58..