Розділ 2. Статистико-економічний аналіз діяльності закладів культури

2.1. Аналіз динаміки чисельності закладів культури та їх відвідування населенням

Вид аналітичної функції, за допомогою якої визначають тенденції розвитку у рядах динаміки, залежить від характеру коливань значень ознаки.

1. Якщо показники динамічного ряду змінюються в арифметичній прогресії, без різких коливань, більш-менш рівномірно, то динамічні ряди вирівнюють за рівнянням прямої лінії. 1, ст. 608

При використанні прямолінійного тренду ŷt = а₀ + а₁t параметри а₀ і а₁ можуть бути знайдені шляхом рішення системи нормальних рівнянь:

nа₀ + а1∑t = ∑y; (2.1)

а₀∑t + а1∑t² = ∑ yt

за формулами : ; (2.2)

.

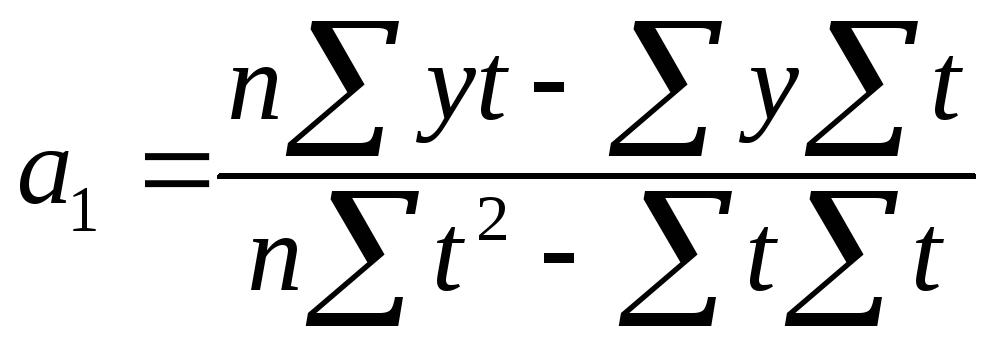На основі даних таблиці 1 визначимо значення параметрів рівняння:

Рівняння прямолінійного тренду прийме вигляд: ŷt = 139-1,4t

Отже, щорічно кількість театрів в середньому знижувалась на 1,4

Підставляючи відповідне даному рокові значення t, визначаємо розрахункові значення ŷt (див. табл. 1.)

Для першого року: у₁ =139-1,4*1=137,6 (од.на рік)

Для другого року: : у₂ = 139-1,4*2=136,2(од. на рік)

Для третього року: = 139-1,4*3=134,8(од.на рік)

Для четвертого року: = 139-1,4*4=133,4(од.на рік)

Для п’ятого року: = 139-1,4*5=132(од.на рік)

2. Якщо зміна рівнів ряду відбувається з приблизно рівномірним прискоренням або уповільненням ланцюгових абсолютних приростів, то динамічні ряди вирівнюють за рівнянням квадратичної параболи. Для розрахунку параметрів параболічного тренду ŷt = а_{0 +} а₁ t + а₂ t² складаємо систему нормальних рівнянь:

nа₀+ а₁∑t + а₂ ∑t² = ∑у;

а₀∑t + а₁∑t^{2 +} а₂∑t³ = ∑ yt; (2.3)

а₀∑t^{2 +} а₁∑t³ + а₂∑t= ∑ yt²

Підставляємо розрахункові дані в систему нормальних рівнянь (див. табл. 1).

Ділимо всі коефіцієнти в рівняннях на відповідні коефіцієнти при а_{0 :}

Віднімаючи від другого рівняння перше, а від третього – друге, отримуємо два рівняння з двома невідомими:

Ділимо кожну складову цих рівнянь на відповідні коефіцієнти при а₁ і віднімаємо від другого рівняння перше.

Звідки

Методом підстановки отримуємо параметри а₀ та а₁:

Отже, рівняння параболічного тренду має вигляд:

ŷt = 139 – 2,259t + 0,17t²

Це означає, що в році, який передує початку досліджень, вирівняна кількість театрів складала 139од., початкова швидкість зниження кількості театрів -2,259од., а прискорення зміни щорічних приростів – 0,17 од. на рік

Підставляючи в отримане рівняння відповідні значення t, визначаємо розрахункові значення показника для кожного року:

ŷ₁= 139,73-2,259*1+0,17*1=137,6(од.на рік)

ŷ₂= 139,73-2,259*2+0,17*4=135,9(од.на рік)

ŷ₃= 139,73-2,259*3+0,17*9= 134,5(од.на рік)

ŷ₄= 139,73-2,259*4+0,17*16=133,4(од.на рік)

ŷ₅= 139,73-2,259*5+0,17*16=132,7(од.на рік)

Розрахункові значення показників наведені в таблиці 1. Близькість розрахункової і фактичної суми у (відповідно 674,1 і 674) є критерієм правильності проведених розрахунків.

Для обґрунтування вибору трендового рівняння визначимо квадрати відхилень фактичних рівнів від розрахункових (див. табл. 2). Порівняльний аналіз одержаних даних показує, що для трендового моделювання більш обґрунтованим є рівняння прямої, оскільки сума квадратів відхилень розрахункових значень від фактичних в даному випадку найменша (674<674,1).

Для екстраполяції (прогнозування) показників на наступні періоди у рівняннях тренду змінюють порядковий номер року та розраховують ŷНаприклад, для 8-го року дослідження при використанні рівняння параболічного тренду отримаємо:

Ŷ₈= 139 – 1,4 *8 = 127,8

Рис. 1 Аналітичне вирівнювання кількості театрів в Україні в період 2009-2013р

Для характеристики рядів динаміки відвідування музеїв використовується система взаємопов’язаних показників: абсолютний приріст, темп зростання, темп приросту і абсолютне значення одного проценту приросту.

Абсолютний приріст характеризує розмір збільшення (або зменшення) рівня показників динамічного ряду за певний період. Його виражають у тих самих одиницях, що й рівні ряду динаміки. Цей показник обчислюють двома способами:

1. якщо кожний рівень ряду динаміки порівнюється з попереднім рівнем, абсолютний приріст називають ланцюговим:

;

2. якщо всі рівні ряду порівнюють з базисним (початковим рівнем), абсолютний приріст називають базисним:

.

Темп зростання – це відношення поточного рівня ряду динаміки () до попереднього () або початкового рівня (). Обчислюється у коефіцієнтах або процентах.

Темп приросту можна визначити віднімаючи від темпу зростання 100%.

Тпр.л. = Тзр.л. – 100%;

Тпр.б. = Тзр.б. – 100%.

Абсолютне значення 1% приросту – це відношення абсолютного приросту за певний період до темпу приросту за той самий період. Цей показник доцільно розраховувати лише для ланцюгових абсолютних приростів і темпів приросту. Простіше його можна визначити як відношення попереднього рівня показника до 100.

Результати розрахунків відображають в таблиці, після якої роблять висновок про зміну показника у часі.

Згідно даних таблиці 4 ,проаналізувавши показники відвідувань музеїв по Україні можна дійти висновку,що кожного року простежується тенденція до зростання відвідувань музеїв (на 100 осіб населення). Найбільша відвідуваність була у період з 2012 по 2013 роки,що на 13,6 % більше ніж у 2009 році.

Таблиця 4

Показники динаміки відвідування музеїв по Україні

Рік	Кількість музеїв од.	Абсолютний приріст од.		Темп зростання,%		Темп приросту,%		Абсолютне значення1% приросту
		б	л	б	л	б	л
2009	45	X	X	100	X	X	X	X
2010	47	2	2	104,4	104,4	4,4	4,4	0,4
2011	48	3	1	106,6	102,1	6,6	2,1	0,5
2012	49	4	1	108,9	102,0	8,9	2,0	0,5
2013	49	4	0	108,9	100,0	8,9	0	0