Примеры решения задач

5. Найти собственные векторы и собственные значения симметричного оператора , действующего в евклидовом пространстве и имеющего в ортонормированном базисе 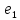, , матрицу

Решение: Характеристический многочлен оператора 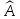имеет вид

,

поэтому , , - собственные значения этого оператора.

Чтобы найти координаты собственных векторов, нужно решить систему уравнений .

При эта система принимает вид

Так как число неизвестных равно 3, а ранг матрицы системы равен 2, то размерность пространства решений равна 1. Следовательно, ФСР состоит из одного решения: . Числа 3, —5, 4 являются координатами собственного вектора в базисе , , , т. е. — собственный вектор оператора . Множество всех собственных векторов оператора , соответствующих собственному значению , задается формулой , где с — любое вещественное число, не равное нулю.

При 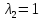эта система принимает вид

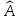Столбец — ФСР этой системы, поэтому множество всех собственных векторов оператора , соответствующих собственному значению , задается формулой , где с — любое число, не равное нулю.

Наконец, при система уравнений относительно координат собственного вектора имеет вид

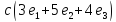Столбец — ФСР этой системы, поэтому множество всех собственных векторов оператора , соответствующих собственному значению , задается формулой , где с — любое число, не равное нулю.

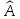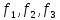6. Линейный оператор , действующий в евклидовом пространстве , имеет в базисе матрицу . Является ли оператор ортогональным, если разложение элементов по ортонормированному базису , , 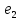имеет вид ?

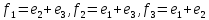Решение: Пусть С — матрица перехода от базиса 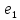, , к базису . Как следует из разложения

По формуле находим матрицу :

Нетрудно проверить, что А_е — ортогональная матрица. Следовательно, 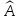— ортогональный оператор.

Тот же результат можно получить иначе, убедившись в том, что имеет место свойство, лежащее в основе определения ортогонального оператора: для верно . С этой целью вычислим вначале скалярное произведение 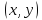, воспользовавшись формулой для скалярного произведения элементов евклидова пространства в произвольном базисе :

, где - координаты элементов x и у в базисе 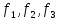. Значения скалярных произведений поместим в следующую таблицу:

	2	1	1
	1	2	1
	1	1	2

Таким образом, имеем

.

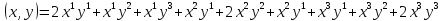Находим столбцы из координат элементов х и и 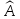у в базисе :

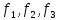Подставляя найденные значения координат в формулу

приходим к равенству . Следовательно, — ортогональный оператор.

Замечание. Хотя — ортогональный оператор, однако его матрица в базисе не является ортогональной. Причина состоит в том, что базис не ортонормированный.