
5. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНЫХ ОПЕРАТОРОВ
5.1
Собственные векторы и собственные
значения. Пусть
линейный оператор
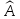 действует в линейном пространстве
действует в линейном пространстве
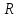 .
.
Определение.
Ненулевой элемент х
из
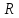 называется собственным
вектором
линейного оператора
называется собственным
вектором
линейного оператора
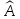 ,
если существует число
,
если существует число
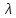 такое, что
такое, что
 .
Число
.
Число
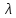 называется при этом собственным
значением оператора
называется при этом собственным
значением оператора
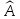 .
Говорят также, что собственный вектор
х
отвечает (или соответствует) собственному
значению
.
Говорят также, что собственный вектор
х
отвечает (или соответствует) собственному
значению
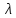 .
.
Свойства собственных векторов и собственных значений линейного оператора.
1°.
Если
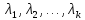 — различные собственные значения
оператора
— различные собственные значения
оператора
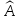 ,
то
отвечающие
им
собственные
векторы
,
то
отвечающие
им
собственные
векторы
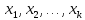 линейно
независимы.
линейно
независимы.
2°.
Линейный оператор, действующий в линейном
пространстве
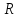 размерности n,
не может иметь более п
различных собственных значений.
размерности n,
не может иметь более п
различных собственных значений.
3°.
Если линейный оператор
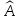 ,
действующий в линейном пространстве
,
действующий в линейном пространстве
 размерности n,
имеет п
различных собственных значений
размерности n,
имеет п
различных собственных значений
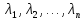 ,
то отвечающие им собственные векторы
,
то отвечающие им собственные векторы
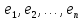 образуют базис пространства
образуют базис пространства
 .
Матрица оператора
.
Матрица оператора
 в этом базисе имеет вид
в этом базисе имеет вид
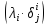 ,
где
,
где
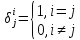 —
символ Кронекера.
—
символ Кронекера.
4°.
Множество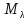 ,
содержащее нулевой элемент и все
собственные векторы линейного оператора
,
содержащее нулевой элемент и все
собственные векторы линейного оператора
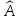 ,
отвечающие собственному значению
,
отвечающие собственному значению
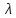 ,
является подпространством линейного
пространства
,
является подпространством линейного
пространства
 .
.
Подпространство
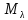 называется собственным
подпространством оператора
называется собственным
подпространством оператора
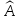 ,
отвечающим собственному значению
,
отвечающим собственному значению
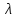 .
.
5.2
Характеристическое уравнение. Пусть
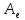 —
матрица
линейного оператора
—
матрица
линейного оператора
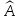 в базисе
в базисе
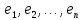 ,
E
- единичная матрица. Составим определитель
,
E
- единичная матрица. Составим определитель
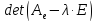 .
Он является многочленом степени п
относительно
.
Он является многочленом степени п
относительно
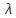 и называется характеристическим
многочленом оператора
и называется характеристическим
многочленом оператора
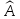 .
.
Уравнение
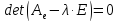 (1)
(1)
называется
характеристическим
уравнением
оператора
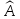 .
.
Характеристический многочлен, а значит, и характеристическое уравнение данного оператора, не зависит от выбора базиса, т. е. в любом базисе коэффициенты характеристического многочлена одни и те же.
Cпособ
отыскания
собственных векторов и собственных
значений линейного оператора
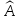 .
.
-
Находим собственные значения оператора, решая уравнение (1). Обозначим их
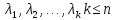 .
. -
Для каждого собственного значения
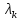 находим все ненулевые решения однородной
системы уравнений
находим все ненулевые решения однородной
системы уравнений
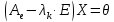 (2)
(2)
Каждое
ненулевое решение X
этой системы является столбцом координат
в базисе
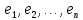 собственного
вектора оператора
собственного
вектора оператора
 ,
соответствующего собственному значению
,
соответствующего собственному значению
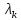 .
.
Замечание.
Собственное значение
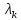 линейного оператора
линейного оператора
 называется
также собственным значением матрицы
называется
также собственным значением матрицы
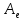 ,
а ненулевое решение системы (2)
(столбец X)
называется собственным вектором матрицы
,
а ненулевое решение системы (2)
(столбец X)
называется собственным вектором матрицы
 .
Во многих разделах математики и ее
приложений рассматриваются именно
собственные значения и собственные
векторы матриц, вне связи их с линейными
операторами.
.
Во многих разделах математики и ее
приложений рассматриваются именно
собственные значения и собственные
векторы матриц, вне связи их с линейными
операторами.
2.3 Инвариантные подпространства линейных операторов.
Определение.
Подпространство М
линейного пространства
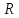 называется
инвариантным
относительно линейного оператора
называется
инвариантным
относительно линейного оператора
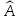 ,
если
для любого элемента х
из М
его образ
,
если
для любого элемента х
из М
его образ
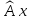 также принадлежит М.
также принадлежит М.
Примеры.
-
Подпространство, состоящее из одного нулевого элемента
 ,
является инвариантным подпространством
относительно любого линейного оператора.
,
является инвариантным подпространством
относительно любого линейного оператора. -
Само линейное пространство
 является инвариантным относительно
любого линейного оператора, действующего
в этом пространстве.
является инвариантным относительно
любого линейного оператора, действующего
в этом пространстве. -
Подпространства
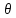 и
и
 называются тривиальными
инвариантными подпространствами
линейного оператора.
называются тривиальными
инвариантными подпространствами
линейного оператора. -
Собственное подпространство
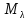 линейного оператора
линейного оператора
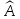 ,
отвечающее
собственному значению
,
отвечающее
собственному значению
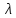 ,
является инвариантным относительно
оператора
,
является инвариантным относительно
оператора
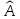 .
. -
Найти собственные векторы и собственные значения линейного оператора
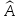 ,
действующего в линейном пространстве
,
действующего в линейном пространстве
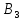 радиус-векторов и имеющего в
ортонормированном базисе
радиус-векторов и имеющего в
ортонормированном базисе
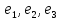 матрицу
матрицу
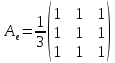 Так как
Так как
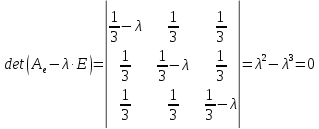
то
характеристическое уравнение оператора
 имеет вид
имеет вид
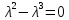 .
Корни этого уравнения
.
Корни этого уравнения
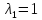 и
и
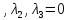 — собственные значения оператора А.
Собственное значение
— собственные значения оператора А.
Собственное значение
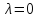 называется двукратным
собственным значением.
называется двукратным
собственным значением.
Чтобы
найти координаты собственных векторов,
нужно решить систему уравнений (2)
при
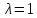 и
и
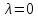
При
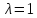 система уравнений (2) принимает вид
система уравнений (2) принимает вид
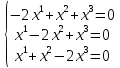
Так
как число неизвестных равно 3, а ранг
матрицы системы равен 2, то размерность
пространства решений равна 1. Решая,
находим фундаментальную систему решений,
состоящую из одного столбца
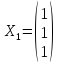 .
Это столбец координат собственного
вектора
.
Это столбец координат собственного
вектора
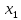 ,
отвечающего
собственному значению
,
отвечающего
собственному значению
 в базисе
в базисе
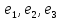 .
Множество всех собственных векторов,
соответствующих собственному значению
.
Множество всех собственных векторов,
соответствующих собственному значению
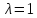 ,
имеет вид
,
имеет вид
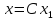 ,
где
,
где
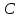 — произвольное вещественное число, не
равное нулю.
— произвольное вещественное число, не
равное нулю.
При
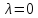 система уравнений (2) принимает вид
система уравнений (2) принимает вид

В этой системе уравнений число неизвестных равно 3, а ранг матрицы системы равен 1. Поэтому размерность пространства решений равна 2. Решая, находим фундаментальную систему решений, состоящую из двух столбцов
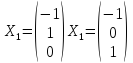 .
.
Эти
столбцы представляют собой координаты
в базисе
 двух линейно независимых собственных
векторов
двух линейно независимых собственных
векторов
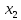 и
и
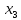 ,
отвечающих
собственному значению
,
отвечающих
собственному значению
 .
Все множество собственных векторов,
соответствующих собственному значению
.
Все множество собственных векторов,
соответствующих собственному значению
 ,
дает линейная комбинация векторов
,
дает линейная комбинация векторов
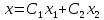 ,
где
,
где
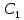 и
и
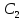 —
произвольные вещественные числа,
одновременно не равные нулю.
—
произвольные вещественные числа,
одновременно не равные нулю.
-
Найти собственные векторы и собственные значения матрицы
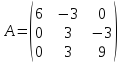
Характеристический многочлен матрицы А имеет вид

Его
трехкратный корень
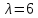 является собственным значением матрицы
А.
Чтобы найти собственные векторы, нужно
решить систему уравнений
является собственным значением матрицы
А.
Чтобы найти собственные векторы, нужно
решить систему уравнений
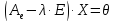

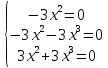
В
этой системе число неизвестных равно
3, а ранг матрицы системы равен 2. Поэтому
размерность пространства решений равна
1. Решая, находим фундаментальную систему
решений, состоящую из одного столбца
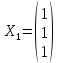 .
Таким образом, множество всех собственных
векторов матрицы А
есть множество столбцов вида
.
Таким образом, множество всех собственных
векторов матрицы А
есть множество столбцов вида
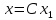 ,
где
,
где
 — произвольное число, не равное нулю.
— произвольное число, не равное нулю.
-
Три материальных точки
 единичной массы соединены между собой
и со стенкой тремя пружинами с
коэффициентами жесткости
единичной массы соединены между собой
и со стенкой тремя пружинами с
коэффициентами жесткости
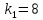 ,
,
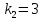 ,
,
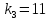 (рис. 4). Найти собственные частоты и
формы малых собственных колебаний
данной системы.
(рис. 4). Найти собственные частоты и
формы малых собственных колебаний
данной системы.
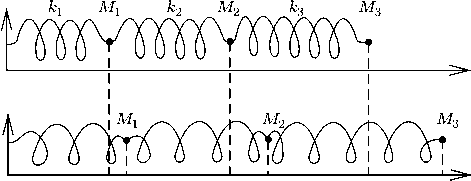
рис. 4
Прежде
всего, уточним постановку задачи.
Положение равновесия материальных
точек
 ,
соответствующее нерастянутым пружинам,
отметим на оси х
точками
,
соответствующее нерастянутым пружинам,
отметим на оси х
точками
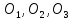 .
Если сжать или растянуть
пружины каким-то образом, а затем
отпустить их, то начнется колебательное
движение системы. Будем пренебрегать
силами
трения и массами пружин. В произвольный
момент времени t
точки
.
Если сжать или растянуть
пружины каким-то образом, а затем
отпустить их, то начнется колебательное
движение системы. Будем пренебрегать
силами
трения и массами пружин. В произвольный
момент времени t
точки
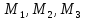 занимают какие-то положения
занимают какие-то положения
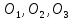 .
Величины направленных отрезков
.
Величины направленных отрезков
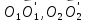 и
и
 на оси x,
характеризующие отклонения точек
на оси x,
характеризующие отклонения точек
 от положения равновесия, обозначим
через
от положения равновесия, обозначим
через
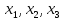 .
Если эти величины изменяются со временем
по закону
.
Если эти величины изменяются со временем
по закону
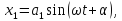
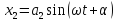 ,
,

то
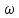 ;
называется собственной
частотой
системы, а отношения
;
называется собственной
частотой
системы, а отношения
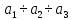 будем называть формой
собственных колебаний,
совершаемых с частотой
будем называть формой
собственных колебаний,
совершаемых с частотой
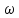 .
.
Для
отыскания собственных частот и
соответствующих им форм колебаний
составим уравнения движения материальных
точек
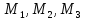 .
На каждую из этих точек действуют силы,
обусловленные жесткостью пружин.
Согласно закону Гука при малом растяжении
пружины упругая сила, стремящаяся
вернуть пружину в первоначальное
(нерастянутое) положение, пропорциональна
величине растяжения. Величины растяжений
первой, второй и третьей пружин в момент
t
равны соответственно
.
На каждую из этих точек действуют силы,
обусловленные жесткостью пружин.
Согласно закону Гука при малом растяжении
пружины упругая сила, стремящаяся
вернуть пружину в первоначальное
(нерастянутое) положение, пропорциональна
величине растяжения. Величины растяжений
первой, второй и третьей пружин в момент
t
равны соответственно
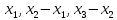 (см. рис. 4). Поэтому на точку
(см. рис. 4). Поэтому на точку
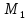 в момент t
со стороны первой пружины действует
сила
в момент t
со стороны первой пружины действует
сила
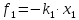 ,
а со стороны второй пружины — сила
,
а со стороны второй пружины — сила
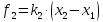 .
Обратите
внимание на знаки выражений для
.
Обратите
внимание на знаки выражений для
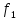 и
и
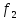 .
Если
.
Если
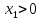 ,
то первая пружина в момент t
растянута по отношению к положению
равновесия, упругая сила стремится
сжать пружину, и, следовательно, на точку
,
то первая пружина в момент t
растянута по отношению к положению
равновесия, упругая сила стремится
сжать пружину, и, следовательно, на точку
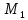 со стороны первой пружины действует
сила, направленная влево, т. е.
со стороны первой пружины действует
сила, направленная влево, т. е.
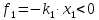 .
Если
.
Если
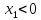 ,
то первая пружина сжата, упругая сила
стремится растянуть ее, и поэтому на
точку
,
то первая пружина сжата, упругая сила
стремится растянуть ее, и поэтому на
точку
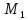 действует сила, направленная вправо,
т. е.
действует сила, направленная вправо,
т. е.
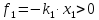 .
Аналогично, если
.
Аналогично, если
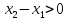 ,
то вторая пружина растянута, сила
упругости стремится сжать ее, и поэтому
со стороны второй пружины на точку
,
то вторая пружина растянута, сила
упругости стремится сжать ее, и поэтому
со стороны второй пружины на точку
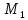 действует сила, направленная вправо:
действует сила, направленная вправо:
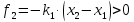 .
То же самое выражение для
.
То же самое выражение для
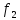 получается
в случае
получается
в случае
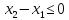 .
.
Итак,
результирующая сила, действующая на
точку
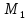 ,
есть сила
,
есть сила
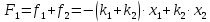
По
второму закону Ньютона произведение
массы точки
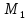 (она равна единице) на ускорение точки
(ускорение есть вторая производная по
времени
от
смещения x)
равно результирующей силе
(она равна единице) на ускорение точки
(ускорение есть вторая производная по
времени
от
смещения x)
равно результирующей силе
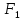

Аналогично,
на точки
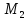 и
и
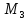 действуют результирующие силы
действуют результирующие силы
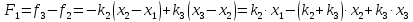
и
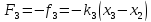 .
.
Поэтому уравнения движения этих точек имеют вид
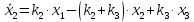 ,
,
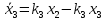
Будем искать решение системы дифференциальных уравнений
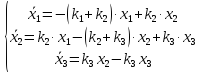
в виде (3). Подставляя (3) в систему, приходим к виду
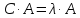 (6)
(6)
где
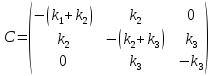 — известная матрица, составленная из
коэффициентов правых частей уравнений,
— известная матрица, составленная из
коэффициентов правых частей уравнений,
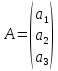 — искомый столбец “амплитуд”,
— искомый столбец “амплитуд”,
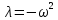 — квадрат искомой собственной частоты,
взятый со знаком минус.
— квадрат искомой собственной частоты,
взятый со знаком минус.
Таким
образом, для отыскания собственных
частот
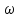 нужно найти собственные значения
нужно найти собственные значения
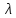 матрицы С,
а для нахождения формы собственных
колебаний нужно найти соответствующие
собственные векторы.
матрицы С,
а для нахождения формы собственных
колебаний нужно найти соответствующие
собственные векторы.
Учитывая,
что
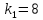 ,
,
 ,
,
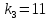 ,
получаем следующее характеристическое
уравнение матрицы С:
,
получаем следующее характеристическое
уравнение матрицы С:
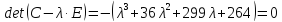
Оно
имеет корни
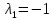 ,
,
 ,
,
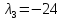 .
Следовательно,
.
Следовательно,
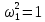 ,
,
 ,
,
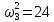 ,
т. е. собственными частотами колебательной
системы будут
,
т. е. собственными частотами колебательной
системы будут
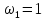 ,
,
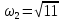 ,
,
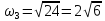
Решая
для каждого собственного значения
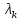 систему
(6),
находим собственные векторы матрицы С
— столбцы
систему
(6),
находим собственные векторы матрицы С
— столбцы
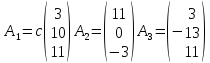
где
с
— произвольное число, не равное нулю.
Отношения элементов столбца
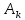 определяют форму собственных колебаний
с частотой
определяют форму собственных колебаний
с частотой
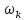 .
Так,
форма собственных колебаний с частотой
.
Так,
форма собственных колебаний с частотой
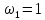 задается отношениями:
задается отношениями:
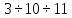 .
.
