
-
В линейном пространстве действует линейный оператор , переводящий ортонормированный базис в элементы такие, что
 ,
,
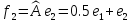 ,
,
 .
.
Найти
все подпространства пространства
 ,
инвариантные относительно оператора
,
инвариантные относительно оператора
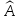 .
.
Прежде
всего укажем тривиальные инвариантные
подпространства
 и
и
 .
Для нахождения остальных инвариантных
подпространств найдем собственные
значения и собственные векторы оператора
.
Для нахождения остальных инвариантных
подпространств найдем собственные
значения и собственные векторы оператора
 .
Характеристический
многочлен матрицы Ае
имеет вид
.
Характеристический
многочлен матрицы Ае
имеет вид

Его
корни
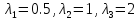 являются собственными значениями
оператора
являются собственными значениями
оператора
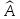 .
.
Чтобы
найти собственные векторы, нужно решить
систему линейных уравнений
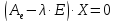 при
при
 ,
равных собственным значениям оператора
,
равных собственным значениям оператора
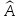 .
При
.
При
 система
принимает вид
система
принимает вид
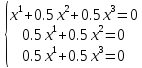
Так
как число неизвестных равно 3, а ранг
матрицы системы равен 2, то размерность
пространства решений равна 1. Решая,
находим фундаментальную систему решений,
состоящую из одного столбца
 .
Это столбец координат собственного
вектора
.
Это столбец координат собственного
вектора
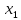 ,
отвечающего
собственному значению
,
отвечающего
собственному значению
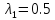 в базисе
в базисе
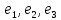 .
Одномерное инвариантное относительно
оператора
.
Одномерное инвариантное относительно
оператора
 подпространство, соответствующее
собственному значению
подпространство, соответствующее
собственному значению
 ,
есть линейная оболочка
,
есть линейная оболочка
 ,
, где с
— произвольное вещественное число.
,
, где с
— произвольное вещественное число.
При
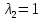 система принимает вид
система принимает вид

Как
и в предыдущем случае, одномерное
инвариантное относительно оператора
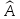 подпространство,
соответствующее собственному значению
подпространство,
соответствующее собственному значению
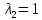 ,
есть линейная оболочка
,
есть линейная оболочка
 ,
где с
— произвольное вещественное число, а
,
где с
— произвольное вещественное число, а
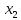 — собственный вектор, отвечающий
— собственный вектор, отвечающий
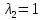 и имеющий в базисе
и имеющий в базисе
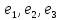 координаты
координаты
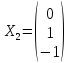 .
.
Наконец,
при
 система принимает вид
система принимает вид
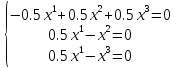
Ранг
матрицы тоже равен 2. Поэтому инвариантное
относительно оператора
 подпространство,
соответствующее собственному значению
подпространство,
соответствующее собственному значению
 ,
имеет размерность 1 и представляет собой
линейную оболочку
,
имеет размерность 1 и представляет собой
линейную оболочку
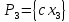 ,
где с
— произвольное вещественное число, а
,
где с
— произвольное вещественное число, а
 — собственный вектор, отвечающий
— собственный вектор, отвечающий
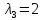 и имеющий в базисе
и имеющий в базисе
 координаты
координаты
 .
.
Далее,
линейные оболочки —
 ,
,
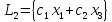 ,,
,,
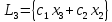 ,,
где
,,
где
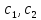 — произвольные вещественные числа,
являются двумерными инвариантными
относительно оператора
— произвольные вещественные числа,
являются двумерными инвариантными
относительно оператора
 подпространствами.
Действительно, например, для
подпространствами.
Действительно, например, для
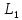 имеем
имеем

Других
инвариантных относительно оператора
 подпространств
нет.
подпространств
нет.
-
Ортогональный оператор.
Определение.
Линейный оператор
 ,
действующий в евклидовом пространстве,
называется ортогональным,
если для любых элементов x,
y
из этого пространства выполняется
равенство (
,
действующий в евклидовом пространстве,
называется ортогональным,
если для любых элементов x,
y
из этого пространства выполняется
равенство ( x,
x,
 у)
=
(х,
у).
у)
=
(х,
у).
Иными
словами, ортогональный оператор
 — это линейный оператор, сохраняющий
скалярное произведение элементов:
скалярное произведение образов
— это линейный оператор, сохраняющий
скалярное произведение элементов:
скалярное произведение образов
 x
и
x
и
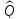 y
равно скалярному произведению их
прообразов x
и у.
y
равно скалярному произведению их
прообразов x
и у.
Свойства ортогонального оператора.
1°.
Ортогональный оператор
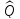 не изменяет нормы элементов, т. е.
не изменяет нормы элементов, т. е.
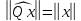 .
.
2°.
Если
 —
ортогональный оператор, то существует
обратный к нему оператор
—
ортогональный оператор, то существует
обратный к нему оператор
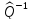 ,
который также является ортогональным,
и справедливо равенство
,
который также является ортогональным,
и справедливо равенство
 ,
(1)
,
(1)
т.
е. обратный оператор к ортогональному
оператору
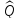 совпадает с сопряженным оператором
совпадает с сопряженным оператором
 ,.
Равенство (1) можно записать в эквивалентных
формах:
,.
Равенство (1) можно записать в эквивалентных
формах:
 ,
или
,
или
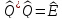 , (2)
, (2)
где
 — тождественный оператор.
— тождественный оператор.
Свойства 1° и 2° являются характеристическими свойствами ортогонального оператора, т. е. линейный оператор, действующий в евклидовом пространстве и не изменяющий нормы элементов, является ортогональным оператором, и точно так же линейный оператор, для которого справедливо равенство (1) или (2), является ортогональным оператором. Поэтому свойства 1° и 2° могут быть положены в основу определения ортогонального оператора.
3°.
Ортогональный оператор переводит
ортонормированный базис в ортонормированный
базис, и, обратно, если линейный оператор
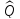 переводит
какой-нибудь ортонормированный базис
в ортонормированный базис, то
переводит
какой-нибудь ортонормированный базис
в ортонормированный базис, то
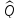 — ортогональный оператор.
— ортогональный оператор.
4°.
В любом ортонормированном базисе матрица
Q
ортогонального оператора является
ортогональной матрицей, т. е. удовлетворяет
условию
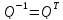 .
Это условие можно записать в эквивалентных
формах:
.
Это условие можно записать в эквивалентных
формах:
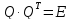 или
или
 .
.
Обратно:
если в некотором ортонормированном
базисе матрица оператора
Q
ортогональная, то
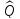 —
ортогональный оператор.
—
ортогональный оператор.
5°.
Если число
 — собственное значение ортогонального
оператора, то
— собственное значение ортогонального
оператора, то
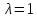 или
или
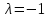 .
.
