
3.2. Неравенство Коши - Буняковского
Теорема
3.1. Для
любых векторов
х,
у
евклидова
пространства
 справедливо
неравенство
Коши - Буняковского
справедливо
неравенство
Коши - Буняковского
 (3.1)
(3.1)
При
 обе части неравенства (3.1) равны нулю
согласно свойству 3.3, значит, неравенство
выполняется. Отбрасывая этот очевидный
случай, будем считать, что
обе части неравенства (3.1) равны нулю
согласно свойству 3.3, значит, неравенство
выполняется. Отбрасывая этот очевидный
случай, будем считать, что .
Для
любого действительного числа
.
Для
любого действительного числа
 ,
в силу аксиомы г), выполняется неравенство
,
в силу аксиомы г), выполняется неравенство
 (3.2)
(3.2)
Преобразуем левую часть неравенства, используя аксиомы и свойства скалярного умножения:
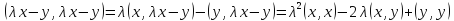
Мы
получили квадратный трехчлен относительно
параметра
 (коэффициент
(коэффициент при
при согласно аксиоме г) ненулевой, так как
согласно аксиоме г) ненулевой, так как ,
неотрицательный
при всех действительных значениях
параметра. Следовательно, его дискриминант
равен нулю или отрицательный, т.е.
,
неотрицательный
при всех действительных значениях
параметра. Следовательно, его дискриминант
равен нулю или отрицательный, т.е.

Что и требовалось доказать.
Доказательство неравенства Коши — Буняковского выглядит достаточно просто. Тем не менее это неравенство очень полезное. Применяя его в конкретных евклидовых пространствах, мы получаем некоторые хорошо известные в анализе и алгебре неравенства.
Пример
3.5. В
случае линейного
арифметического пространства
 неравенство Коши — Буняковского
трансформируется в неравенство
Коши:
неравенство Коши — Буняковского
трансформируется в неравенство
Коши:

В
евклидовом пространстве
 ,
скалярное произведение в котором
выражается определенным интегралом
(см. пример 3.4), неравенство Коши —
Буняковского превращается в
неравенство Буняковского (называемое
также неравенством
Шварца):
,
скалярное произведение в котором
выражается определенным интегралом
(см. пример 3.4), неравенство Коши —
Буняковского превращается в
неравенство Буняковского (называемое
также неравенством
Шварца):

3.3. Нормированные пространства
В
линейном
пространстве обобщением
понятия длины свободного
вектора является
норма. Длину вектора в линейном
пространстве
 или
или можно
рассматривать как функцию, определенную
на множестве
можно
рассматривать как функцию, определенную
на множестве
 (соответственно
(соответственно
 ),
которая
каждому вектору ставит в соответствие
число — его длину. Норму вектора в
линейном пространстве иногда называют
длиной, имея в виду связь с аналогичным
термином векторной алгебры.
),
которая
каждому вектору ставит в соответствие
число — его длину. Норму вектора в
линейном пространстве иногда называют
длиной, имея в виду связь с аналогичным
термином векторной алгебры.
Определение
3.2. Функцию,
заданную на линейном пространстве
 ,
которая каждому вектору
,
которая каждому вектору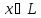 ставит
в соответствие действительное число
ставит
в соответствие действительное число
 ,
называютнормой,
если
она удовлетворяет следующим аксиомам
нормы:
,
называютнормой,
если
она удовлетворяет следующим аксиомам
нормы:
а)
 ,
причем равенство
,
причем равенство возможно только при
возможно только при ;
;
б)
 ;
;
в)
 (неравенство
треугольника).
(неравенство
треугольника).
Определение 3.3. Линейное пространство, в котором задана норма, называют нормированным пространством.
Евклидовы пространства и нормированные пространства представляют собой примеры линейных пространств с дополнительными структурами: скалярным умножением и нормой соответственно. Эти два понятия совершенно различны, однако, как утверждает следующая теорема, исходя из скалярного умножения в евклидовом пространстве можно задать норму и тем самым превратить евклидово пространство в нормированное.
Теорема 3.2. Всякое скалярное умножение в евклидовом пространстве определяет норму согласно формуле
 (3.3)
(3.3)
Отметим,
что, согласно аксиоме г) скалярного
умножения,
 и, следовательно, функция, заданная
соотношением (3.3), определена для всех
векторовх
евклидова
пространства. Проверим выполнение
аксиом нормы. Аксиома а) нормы немедленно
следует из аксиомы г) скалярного умножения
(определение 3.1). Аксиома б) нормы вытекает
из аксиомы в) скалярного умножения и
свойства 3.1:
и, следовательно, функция, заданная
соотношением (3.3), определена для всех
векторовх
евклидова
пространства. Проверим выполнение
аксиом нормы. Аксиома а) нормы немедленно
следует из аксиомы г) скалярного умножения
(определение 3.1). Аксиома б) нормы вытекает
из аксиомы в) скалярного умножения и
свойства 3.1:

Остается проверить аксиому в) нормы, для чего мы воспользуемся неравенством Коши — Буняковского (3.1),
 ,
,
которое можно записать в виде

или, с учетом (3.3),
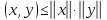 .
.
Используя это неравенство, получаем


Что и требовалось доказать.
Введение нормы по формуле (3.3) опирается только на общие свойства скалярного умножения, вытекающие из его аксиом, и не связано со спецификой конкретного линейного пространства. Поэтому такую норму в евклидовом пространстве называют евклидовой или сферической нормой. Когда говорят, не уточняя, о норме в евклидовом пространстве, обычно имеют в виду именно эту норму.
Вовсе не обязательно, чтобы в евклидовом пространстве норма вводилась через скалярное произведение. Рассмотрим следующие примеры, показывающие другие часто используемые нормы, не связанные с каким-либо скалярным произведением.
Пример
3.6. В
линейном
арифметическом пространстве
 нормой
является функция
нормой
является функция
 вида
вида
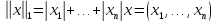
( в
правой части обозначает модуль
действительного числа).
в
правой части обозначает модуль
действительного числа).
Легко убедиться, что аксиома а) нормы выполнена, так как величина
 ,
причем она равна нулю тогда и только
тогда, когда все компоненты
,
причем она равна нулю тогда и только
тогда, когда все компоненты
 арифметического
вектора равны нулю.
арифметического
вектора равны нулю.
Так
же просто убедиться в верности аксиомы
б) нормы. Для проверки неравенства
треугольника (аксиома в) нормы) выберем
произвольные два вектора и
и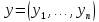 из
из
 .
Тогда
.
Тогда


Приведенную
норму называют
 -нормой
или
октаэдрической
нормой.
-нормой
или
октаэдрической
нормой.
Пример 3.7. Функция
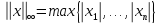
заданная
на векторах
 в
в
 ,
также
является нормой в
,
также
является нормой в
 .
Эту
норму называют
.
Эту
норму называют
 --нормой
или
кубической
Нормой.
--нормой
или
кубической
Нормой.
Как
и в предыдущем примере проверка аксиом
а) и б) нормы очевидна. Проверим неравенство
треугольника для произвольных векторов и
и из
из
 :
:



Нормы
 одного
и того же вектора х
связаны
неравенствами
одного
и того же вектора х
связаны
неравенствами
 .
.
которые непосредственно вытекают из определений этих норм.
Пример
3.8. Множество
S
тех векторов х
нормированного
пространства, которые удовлетворяют
равенству
 (единичных
векторов), называют
единичной
сферой. Множество
S
зависит от линейного пространства и
однозначно определяет рассматриваемую
в нем норму. На рис. 3.1 изображен вид
единичной сферы для различных норм
двумерного линейного пространства
(конкретно линейного пространства
радиус-векторов точек плоскости):
евклидовой (рис. 3.1, а),
ок-таэдрической (рис. 3.1,6) и кубической
(рис. 3.1, в). В случае трехмерного линейного
пространства (линейного пространства
радиус-векторов) единичные сферы
указанных норм изображены на рис. 3.2. Мы
видим, что это сфера (рис. 3.2, а),
октаэдр (рис. 3.2, 6)
и
куб (рис. 3.2, в).
Вид единичной сферы для этих норм и
послужил источником для их названий.
(единичных
векторов), называют
единичной
сферой. Множество
S
зависит от линейного пространства и
однозначно определяет рассматриваемую
в нем норму. На рис. 3.1 изображен вид
единичной сферы для различных норм
двумерного линейного пространства
(конкретно линейного пространства
радиус-векторов точек плоскости):
евклидовой (рис. 3.1, а),
ок-таэдрической (рис. 3.1,6) и кубической
(рис. 3.1, в). В случае трехмерного линейного
пространства (линейного пространства
радиус-векторов) единичные сферы
указанных норм изображены на рис. 3.2. Мы
видим, что это сфера (рис. 3.2, а),
октаэдр (рис. 3.2, 6)
и
куб (рис. 3.2, в).
Вид единичной сферы для этих норм и
послужил источником для их названий.

рис. 3.1

рис. 3.2
