fizpr

затем пропустить оба луча через анализатор, у которого плоскость колебаний, например, перпендикулярна РР, то луч левой половины поля зрения С будет погашен и поле зрения в этой половине будет темное, тогда как часть света правой половины будет пропущена анализатором и поле этой половины будет светлое. Если плоскость колебаний, пропускаемых анализатором, перпендикулярна Р1Р1, то будет обратное явление. В среднем положении анализатора, при котором обе половины поля зрения будут одинаково освещены, получим «нулевую точку».

При помещении трубки Т с раствором сахара в камеру сахариметра между полутеневой пластинкой из кварца и анализатором (рис.2), предварительно установленным на нулевую точку, равномерная освещенность поля зрения нарушается. Угол, на который надо повернуть анализатор, чтобы достигнуть первоначальной одинаковой освещенности двух половин поля зрения, очевидно, равен углу поворота φ плоскости поляризации оптически активным ратвором. (1) .

Для измерения угла φ при пользовании источником белого света вводят специальное приспособление - кварцевый компенсатор К (рис. 2). Он состоит из двух клиньев, сделанных из левовращающего кварца. Один клин K1 неподвижный, второй К2 - подвижный. Перемещая К2 относительно K1, можно изменять толщину К и, следовательно, величину левого вращения плоскости поляризации (1), даваемого кварцевыми клиньями K1 и К2 (их общей толщиной).

Так как раствор сахара вращает плоскость поляризации вправо (по часовой стрелке), то это вращение компенсируется левым

191

вращением кварцевого компенсатора К, удельное вращение которого примерно такое же, как у сахара для всех длин волн белого света.

Подвижный клин К2 кварцевого компенсатора перемещается вместе со шкалой. Линейное перемещение этого клина пропорционально углу вращения плоскости поляризации раствором сахара. Шкала прибора проградуирована в угловых единицах, называемых градусами Вентцке (1° Вентцке = 0,328 углового градуса). Для более точного отсчета шкала имеет нониус.

По измеренному углу φ поворота плоскости поляризации при известном значении постоянной прибора k и длине l трубки с раствором сахара можно определить его концентрацию С из соотношения:

Порядок выполнения работы

1.Включить осветитель в сеть.

2.Установить окуляр поля зрения и расположенный над ним окуляр шкалы сахариметра по глазу наблюдателя так, чтобы в первом была четко видна вертикальная линия, разделяющая поле зрения на две полуокружности, а во втором штрихи и цифры шкалы компенсатора и нониуса.

3.Произвести установку поляризатора на нуль, медленно вращая головку кремальерной передачи. При этом в окуляре поля зрения получается равная освещенность обеих полуокружностей поля

192

зрения, а в окуляре шкалы сахариметра нуль шкалы и нуль нониуса должны совпасть.

4.Визуально убедиться, что в трубках с растворами сахара нет пузырьков воздуха.

5.В сахариметр поместить трубку с раствором сахара известной концентрации С1, при этом равная освещенность поля зрения нарушается. При помощи кремальерной передачи вновь добиться равной освещенности поля зрения и взять отсчет угла φ1 по шкале, наблюдаемой в окуляре шкалы сахариметра (относительно неподвижной шкалы нониуса). Результат занести в таблицу.

6.Повторить п. 3 и п.5 для всех трубок с известными концентрациями растворов сахара.

7.Из формулы (1) получить выражение для постоянной прибора k. Вычислить и записать в таблицу 5 ее значения для растворов известной концентрации при длине пути луча в растворе (длине трубки) l = 20см. Найти среднее арифметическое значение постоянной прибора

8.Поместить в сахариметр трубку с раствором сахара неизвестной концентрации и произвести замер угла φx согласно п. З и 5. По формуле (2) вычислить неизвестную концентрацию Сx раствора сахара, используя среднее значение постоянной прибора kcp и длину пути луча в этом растворе l (п. 7).

193

1.Что собой представляет свет с точки зрения волновой теории?

2.Какой свет называется: естественным, поляризованным, плоскополяризованным, поляризованным по кругу (см. лаб. раб.

№ 504)?

3.В чем заключается явление двойного лучепреломления? Чем отличается обыкновенный луч от необыкновенного (лаб. раб. № 504)?

4.Как устроена поляризационная призма Николя?

5.В чем заключается явление вращения плоскости поляризации? Объяснение этого явления по Френелю. Какие вещества называются оптически активными? Приведите примеры таких веществ.

6.От чего зависит угол поворота плоскости поляризации?

7.Какова оптическая схема сахариметра, каково назначение ее элементов?

194

Лабораторная работа № 506

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ СТЕФАНА-БОЛЬЦМАНА ПРИ ПОМОЩИ ОПТИЧЕСКОГО ПИРОМЕТРА

Цель работы: ознакомление с одним из оптических методов измерения температуры и определение постоянной в законе СтефанаБольцмана.

Приборы и принадлежности: лампа накаливания с вольфрамовой нитью, реостат, амперметр, вольтметр, оптический пирометр с исчезающей нитью, трансформатор, выпрямитель.

Основные требования к теоретической подготовке: при подготовке к лабораторной работе необходимо проработать разделы курса общей физики "Тепловое излучение и его характеристики", "Законы теплового излучения" и методические указания к данной работе.

Теория метода и описание установки

Электромагнитное излучение всех длин волн обусловливается колебаниями электрических зарядов (электронов, ионов), входящих в состав вещества. Излучение тела сопровождается потерей энергии. Для того чтобы обеспечить возможность длительного излучения энергии, необходимо пополнять ее убыль. В противном случае

195

излучение будет сопровождаться какими-либо изменениями внутри тела, и состояние излучающей системы будет непрерывно изменяться. Указанные процессы могут быть весьма разнообразны и, следовательно, может быть различен характер и вид излучения (свечения)..

Электромагнитное излучение, которое обусловлено возбуждением атомов или молекул тела вследствие их теплового движения, т.е. их внутренней энергией, называется тепловым (температурным) излучением. Это излучение свойственно всем телам, имеющим температуру выше 0 К.

Только тепловое излучение равновесно. При помещении нагретого тела в полость с идеально отражающими стенками между телом и излучением устанавливается равновесие, т.е. тело в единицу времени будет поглощать столько же энергии, сколько и излучать.

Интенсивность теплового излучения и его спектральный состав зависят от температуры, химической природы и агрегатного состояния нагретого тела.

Все раскаленные твердые и жидкие тела дают сплошной спектр излучения (в спектре присутствуют волны всех длин).

Характеристики теплового излучения.

Спектральная излучательность тела r - мощность излучения с единицы площади поверхности тела в интервале частот (или длин волн) единичной ширины

196

где dWνизл,ν +dν - мощность электромагнитного излучения,

испускаемого с единицы поверхности тела в интервале частот от ν до ν+dν.

Интегральная излучательность (энергетическая светимость) RT – мощность электромагнитного излучения, испускаемого с единицы поверхности тела во всем диапазоне частот (или длин волн).

Интегральная и спектральная излучательность связаны соотношением

∞

RT = ∫ rν ,T dν .

0

Спектральная поглощательная способность тела aυ,T есть безразмерная величина, показывающая, какую долю энергии падающего излучения в интервале частот от ν до ( ν+dν) тело поглощает

Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется абсолютно черным (а.ч.т.). Поглощательная способность (2) а.ч.т. для всех частот (или длин волн) и температур aυ,T = 1. Абсолютно черных тел в природе не существует. Тело, близкое к а.ч.т. по своим свойствам, можно создать искусственно.

197

Для реальных («серых») тел поглощательная способность одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела. Для них aсυ,T =aТ = const < 1.

Законы теплового излучения.

Закон Кирхгофа. Отношение спектральной излучательности к спектральной поглощательной способности тела не зависит от природы тела, оно является для всех тел универсальной функцией частоты (длины волны) и температуры

Универсальная функция Кирхгофа rνа.T.ч.т. - есть не что иное,

как спектральная излучательность а.ч.т., так как для него аυ,T = 1.

Закон Стефана-Больцмана. Интегральная излучательность (энергетическая светимость) а.ч.т. пропорциональна четвертой степени его термодинамической температуры

где σ = 5,672·10-8 Bm/м2·K4 - коэффициент пропорциональности,

который носит название постоянной Стефана-Больцмана.

Если излучение происходит в среде, имеющей температуру Т0, то отдача телом тепла (энергии) Q в единицу времени с единицы площади поверхности по закону Стефана-Болъцмана

198

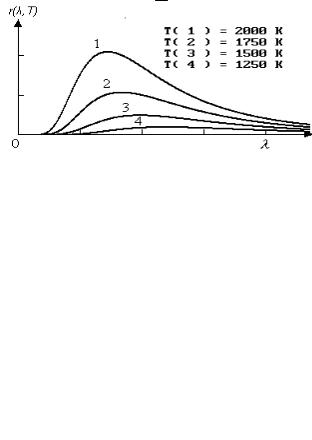
Закон смещения Вина (первый закон Вина). Длина волны λmax, соответствующая максимальной спектральной излучательности а.ч.т., обратно пропорциональна его абсолютной температуре (рис.1):

λmax = b ,

T

где b = 2,89·10-3 м ·K - постоянная Вина.

Второй закон Вина. Максимальная спектральная излучательность а.ч.т. пропорциональна пятой степени абсолютной температуры

(rν ,T ) max = b2T 5 ,

где b2 = 1,29· 10-5 Вт / (м3 К5 )..

Рисунок 1

199

Формула Планка. На основе квантовых представлений об излучении и поглощении электромагнитного излучения атомами и молекулами тел аналитическое выражение универсальной функции Кирхгофа, полученное Планком, имеет вид

где h = 6,62·10-34 Дж·с - постоянная Планка.

Совокупность методов измерения высоких температур, основанных на законах теплового излучения, в частности на использовании зависимости излучательности тела от его температуры, называется оптической пирометрией. Приборы, которые применяются в оптической пирометрии, называются пирометрами излучения. Они бывают двух видов: радиационные и оптические. В радиационных пирометрах регистрируется интегральное тепловое излучение исследуемого нагретого тела. В оптических пирометрах — излучение в каком-либо узком интервале частот (длин волн) т.е. монохроматическое излучение.

Под яркостной температурой Тя, измеряемой оптическими пирометрами, понимается такая температура а.ч.т., при которой его спектральная излучательность (излучательность для определенной

< 1 , то r(ν0 ,Тя) < r(ν0 ,T) , следовательно, Tя< Т.

200