fizpr

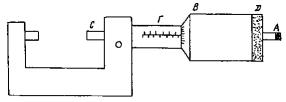
полном обороте барабана его край смещается на 0,50 мм основной шкалы. Поскольку шкала барабана имеет 50 делений, то цена деления этой шкалы равняется 0,01 мм. При завинченом винте нуль барабана стоит против нуля основной шкалы. Основная шкала имеет два масштаба: верхний и нижний. Нижний разбит на сантиметры и миллиметры. Верхний масштаб смещен относительно нижнего на 0,5 мм. Измеряемый предмет помещают между винтом и упором и подводят винт к соприкосновению с предметом. Для создания равномерного давления винта на измеряемый объект микрометр обеспечен специальным приспособлением - трещеткой, которая не допускает очень сильного давления.

Рисунок 2 - Микрометр

При измерении с помощью микрометра могут наблюдаться два случая:

1)Измеряемый предмет имеет длину, которая равняется а целых миллиметров и несколько сотых долей миллиметра, значения которых лежат в интервале от а до (а+0,50) мм. В этом случае сотые доли миллиметра прямо приписываются к целым мм.

2)Измеряемый предмет имеет длину, которая равняется (а+0,5) целых миллиметров и несколько сотых долей миллиметра, значения которых лежат в интервале от (а+0,50) до (а+1) мм. В этом случае

11

сотые доли миллиметра приписываются к (а+0,5) мм.

Какой из этих случаев имеет место, судят по верхней шкале. Если край барабана стоит ближе к делению нижней основной шкалы, то это первый случай, если же к делению верхней - это второй.

Рычажные весы

Перед взвешиванием нужно проверить "нуль" весов, для этого, повернув ручку аретира левой рукой, "открыть" весы (снять весы с аретира). Если стрелка колеблется в пределах шкалы, весы готовы к работе. При взвешивании на рычажных весах любого типа на левую чашку весов (при закрытых весах) помещают груз, а правой рукой на правую чашку помещают разновесы.

Внимание! Весы снимают с аретира только для того, чтобы выяснить, находятся ли нагруженные чашки в равновесии.

Не отпуская аретира, слегка приоткрывают весы, чтобы выяснить, которая из чашек перевешивает. Потом весы закрывают и изменяют набор гирь. Так повторяют до тех пор, пока не установятся плавные колебания стрелки в пределах шкалы.

Максимальная точность взвешивания на технических весах - 10 миллиграмм.

4.Обработка результатов измерений

4.1Измерение физических величин

Изучение физических явлений сопровождается измерениями физических величин, которые характеризуют определенные отношения между предметами или явлениями. Измерить какуюнибудь величину, значит сравнить ее с другой однородной величиной,

12

которая принята за единицу измерений. Экспериментатор должен: а) выбрать метод измерения; б) подобрать и установить измерительные приборы; в) провести наблюдение и отсчет измеренных величин.

Измерения бывают:

прямые, при которых отсчет по шкале прибора непосредственно дает искомую величину (например: измерение длин измерительными приборами, промежутков времени часами, массы весами или измерение температуры термометрами).

косвенные, при которых искомая величина "х" исчисляется по известной зависимости х = f(a, b… ),где величины a, b , ... значение величин, которые получены прямыми измерениями (например, определение плотности тел по формуле, в которую входят значения величин массы и объема, полученные прямыми измерениями).

Измерения принципиально не могут быть абсолютно точными. Любое, даже самое тщательное измерение, всегда сопровождается погрешностями.

Различают ошибки грубые, систематические и случайные.

1)Грубые ошибки (промахи) – это ошибки, которые возникли в результате небрежности отсчета по приборам или неразборчивости записи их показаний. Такой результат необходимо отбросить, а само измерение повторить.

2)Систематические ошибки являются следствием неисправности прибора, неточности метода измерения и т.п. В данном эксперименте они остаются постоянными: имеют одинаковую величину и знак и не уменьшаются при увеличении количества измерений. Систематические ошибки можно учесть, но уменьшить их

величину можно, только улучшив методику измерений. 13

3) Случайными ошибками называются неизбежно возникающие при измерениях сравнительно небольшие погрешности, которые обусловлены субъективными причинами, и которые невозможно заранее учесть. Эти погрешности подчиняются статистическим закономерностям и описываются теорией вероятности. Увеличение количества измерений приводит к уменьшению случайных погрешностей.

Полученные несколько значений измеренной величины отличаются друг от друга за счет случайных погрешностей и составляют выборку - совокупность конечного числа значений случайной величины. В связи с тем, что распределение случайных величин описывается статистическими (вероятностными) законами, то широко используется понятие "вероятности".

Вероятностью называется отношение числа благоприятных событий к полному числу событий. Она может принимать значение от нуля до единицы и утверждение, "значения равновероятны", означает, что они повторяются одинаково часто.

4.2. Гистограмма и ее построение

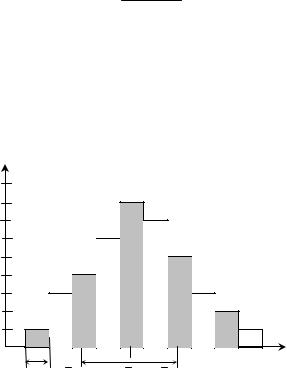
Пусть есть выборка из n значений измеренной величины. Для того, чтобы получить первое представление о распределении этой величины, строят так называемую гистограмму. Гистограмма это ступенчатый график (диаграмма), для построения которой по оси абсцисс откладывают значение измеренной величины, разбитое на интервалы (бины), а по оси ординат - количество n значений этой величины, которые попадают в каждый бин. По оси ординат могут быть отложены также вероятности n /n попадания измеренного

14

Построив гистограмму, можно сделать вывод о следующих закономерностях процесса измерения, которые обусловлены влиянием случайных погрешностей на значение измеренной величины:

1)наиболее часто встречаются величины, которые близки к среднему значению - они наиболее вероятны;

2)величины, одинаково отличающиеся от среднего значения, встречаются одинаково часто – они равновероятны;

3)величины, значительно отличающиеся от среднего значения, маловероятны.

Если увеличивать объем выборки и уменьшать ширину бинов, то ломаная линия в предельном случае превращается в плавную симметричную кривую, которая имеет вид колокола.

4.3 Нормальное распределение и его характеристики

Рассматривая случайные погрешности как один из видов случайных событий, немецкий математик Гаусс установил закон распределения погрешностей измерений в зависимости от своей величины. Этот закон называется законом нормального распределения или распределением Гаусса. На рисунке 4 приведена кривая, которая отвечает этому закону.

Кривая показывает:

1) наиболее вероятные случайные погрешности, близкие к

нулю;

2)с увеличением величины погрешности вероятность их появления быстро уменьшается;

3)погрешности, равные по величине, но противоположные по

16

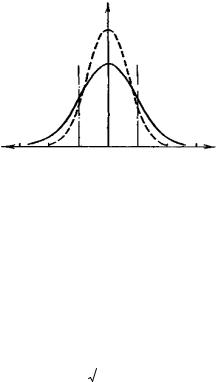
знаку, ровновероятны; 4) при измерениях с одинаковой точностью наиболее

возможным значением измеренной величины есть среднее арифметическое из всех результатов.

f(x)

-3σ -2σ -σ 0 σ 2σ 3σ

Отклонение от действительного значения

Рисунок 4 - График нормального распределения Кривая нормального распределения отвечает теоретическому

случаю бесконечно большого количества измерений n, при котором величины погрешностей неотрывно заполняют всю область значений

±Δх. Аналитическое выражение, которое описывает кривую нормального распределения (закон Гаусса) имеет вид:

где σ2 – дисперсия распределения величины Δх. Из теории следует, что при n >30

где xi = x − xi - отклонение значения измеренной величины от среднего, которое называется случайной абсолютной погрешностью единичного измерения.

Величину σ 2 называют дисперсией, а σ - генеральной

среднеквадратичной погрешностью.

При довольно точных измерениях величина σ мала, а при грубых измерениях наблюдается большой разброс результатов, и значение σ будет большим. В случае реального количества измерений их количество всегда будет конечным. В этом случае не имеет смысла говорить о вероятности появления погрешности данной величины, а говорят о вероятности появления погрешности, которая лежит в пределах некоторого интервала ± х. Интервал ± х называется доверительным, а вероятность Р попадания любого значения измеренной величины в доверительный интервал, называется

доверительной вероятностью или надежностью.

Расчеты площадей, ограниченных кривой распределения, для

Для обычных измерений можно ограничиться Р = 0,95. Для измерений, в которых необходима высокая надежность, задают Р = 0,98.

4.4. Расчет случайной погрешности по методу Стьюдента

В условиях физического практикума тяжело проводить измерение больше 3...5 раз. В этом случае необходимо использовать

18

методику, предложенную в 1908 году английским ученым У. Гассетом (псевдоним - Стьюдент). Он доказал, что статистический подход в достаточной мере возможен и при малом числе измерений (n <30).

Для оценки точности конечного числа измерений вместо σ пользуются выборочным средне квадратичным отклонением среднего арифметического

n

∑( xi )2

Величина, которая равняется отношению

называется коэффициентом Стьюдента. Ниже в таблице 1 приведенны значения коэффициента Стьюдента для любых n и Р

Таблица 1 - Значение коэффициента Стьюдента

19

4.5. Порядок расчета погрешностей прямых измерений

Для расчета случайных погрешностей используем некоторые следствия из распределения Стьюдента, которое применяется для малых выборок. Пусть мы имеем выборку из n значений величины х, разных за счет случайных погрешностей, т.е. имеем ряд значений х1, х2,.....хn. Для предварительной оценки необходимо отвергнуть сомнительные результаты (промахи). После этого можно приступить к выполнению расчета погрешности в следующем порядке:

3) найти среднее квадратичное отклонение среднего арифметического (для оценки точности конечного числа измерений вместо σ пользуются выборочной средней квадратичной ошибкой среднего арифметического)

n

∑( xi )2

S(x) = i=1

n(n − 1)

4) задать доверительную вероятность Р (экспериментатор выбирает по своему усмотрению по обыкновению в пределах от 0,9 до

0,99);

20