fizpr

обратимости хода световых лучей в геометрической оптике (см. на рис.2 и рис.3 ход лучей 3 и 3').

В поле зрения трубы Т рефрактометра, поставленной на пути лучей, прошедших систему двух призм, наблюдаются две области: одна светлая, куда преломленные лучи проходят (нижняя половина), другая темная, куда лучи не проходят. Положение границы светотени, наблюдаемой через окуляр рефрактометра, определяет предельный угол inp, величина которого зависит от плотности (концентрации) исследуемого раствора. Он же определяет показатель преломления раствора n21 (1).

Для разных длин волн света показатели преломления различны (явление дисперсии). Поэтому при освещении призм рефрактометра естественным светом граница светотени будет окрашена в разные цвета и не будет отчетливо резкой. Устранить эту окрашенность можно вращением на рефрактометре дисперсионного кольцакомпенсатора (см. указания на лабораторном стенде).

В окуляре трубы зрения рефрактометра имеется две шкалы: показателя преломления n0 (слева) и процентного содержания сухих веществ 0% (справа), а также перекрестие сетки. Отсчет соответствующих величин производится по положению границы светотени, совмещенной с центром перекрестия сетки.

Порядок выполнения работы

1. Включить рефрактометр в сеть.:

151

а) открыть верхнюю камеру и промыть дистиллированной водой поверхности осветительной и измерительной призм, затем вытереть их насухо чистой салфеткой;

б) нанести на плоскость измерительной призмы две-три капли дистиллированной воды и закрыть верхнюю камеру;

в) перемещением рукоятки с окуляром установить границу светотени так. чтобы она совпадала с центром перекрестия сетки. На шкале показателя преломления определить nо, которое соответствует значению абсолютного показателя преломления дистиллированной воды.

При правильной установке нуль-пункта граница светотени должна совпадать с центром перекрестия сетки) и с 0% шкалы процентного содержания сухих веществ.

2.Выполнить измерения показателей преломления растворов сахара с известной концентрацией (лучше в порядке ее возрастания). Для чего перед каждым измерением промывать дистиллированной водой и насухо вытирать чистой салфеткой поверхности призм. Заполнять пространство между призмами одним из растворов с известной концентрацией (смотри п. 1 б). Записывать в таблицу 1 значения показателя преломления, соответствующие в каждом опыте новому положению границы светотени, совпадающей с центром перекрестия сетки, указывающим по шкале 0% процентное содержание исследуемого раствора.

3.Последним выполнить замер показателя преломления раствора с неизвестной концентрации Сx.

152

ВНИМАНИЕ! Перед замером не забудьте промыть поверхность призм дистиллированной водой.

4.Построить график зависимости показателя преломления растворов с известной концентрацией сахара от величины их концентрации, выраженной в %.

5.По графику найти неизвестную концентрацию Сx раствора, для чего использовать значение его показателя преломления, отмеченное ранее в таблице 1.

6.Сделать вывод о зависимости показателя преломления раствора от его концентрации. Указать величину найденной в работе неизвестной концентрации раствора сахара. Сравнить ее с концентрацией этого же раствора, полученной по шкале 0% рефрактометра.

Таблица 1 - Результаты измерений

*) В заштрихованных ячейках истинные показатели для сравнения

153

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Сформулируйте законы геометрической оптики.

2.Что называется абсолютным и относительным показателем преломления?

3.В чем заключается принцип обратимости хода световых лучей в геометрической оптике?

4.Объясните явление полного внутреннего отражения. При каких условиях оно возможно?

5.Что такое предельный угол полного внутреннего отражения? От чего зависит его значение?

6.Объясните образование темной и светлой областей, наблюдаемых в окуляре рефрактометра (при наличии жидкости между осветительной и преломляющей призмами).

7.Каково соотношение между абсолютными показателями преломления и скоростями распространения света для сред с

разной плотностью?

8. .Какова зависимость показателя преломления раствора от его концентрации?

9.Каковы возможности рефрактометрического метода исследования веществ? Что лежит в его основе?

154

Лабораторная работа № 502

ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ ПРИ ПОМОЩИ ИНТЕРФЕРЕНЦИОННЫХ КОЛЕЦ НЬЮТОНА

Цель работы: изучение явления интерференции света, ознакомление с методикой интерференционных измерений, определение радиуса кривизны линзы при помощи интерференционных колец Ньютона.

Приборы и принадлежности: приспособление для получения колец Ньютона, измерительный микроскоп с осветителем.

Основные требования к теоретической подготовке: при подготовке к лабораторной работе необходимо проработать разделы курса общей физики "Интерференция света" и методические указания к данной работе.

Теория метода и описание установки

При наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Это явление называется интерференцией света.

155

Волны когерентны, если они монохроматичны (одинаковой длины волны) и имеют постоянную, не изменяющуюся со временем разность фаз.

Геометрическая разность хода двух интерферирующих волн

равна

(x2 - x1)

где x1 и x2 - расстояния, которые проходят волны от источника до точки наблюдения.

Оптическая разность хода интерферирующих волн, распространяющихся в среде, отличной от вакуума (воздуха), не равна геометрической.

Оптическая разность хода двух волн, распространяющихся в

где х1п и x2п - оптические пути первой и второй волны.

При отражении от оптически более плотной среды фаза световой волны изменяется на противоположную, что соответствует потере полуволны λ/2. Это равносильно увеличению оптического пути на λ/2, что обязательно должно учитываться при вычислении .

Интерференционные максимумы (максимумы интенсивности света) наблюдаются в тех местах интерференционной картины, в которых оптическая разность хода интерферируемых волн кратна четному числу полуволн или целому числу длин волн, т.е.

где т = 0,1,2,... - порядок интерференционного максимума. В этих точках интерферирующие волны имеют одинаковые фазы.

Интерференционные минимумы (минимумы интенсивности света) наблюдаются в тех местах интерференционной картины, в которых оптическая разность хода интерферирующих волн кратна нечетному числу полуволн, т.е.

где т = 0,1,2,... - порядок интерференционного минимума. В этих точках волны имеют противоположные фазы.

Во всех интерференционных схемах получения когерентных волн выполняется искусственное разделение световых волн, исходящих от одного источника, с последующим наложением их. В областях наложения волны дают устойчивую интерференционную картину в виде чередующихся светлых, соответствующих максимумам, и темных, соответствующих минимумам интенсивности, полос или колец.

Предлагаемый способ наблюдения интерференции света осуществляется при отражении падающего света (луч 1) от верхней (луч 1') и нижней (луч 1'') границ тонкой воздушной прослойки толщиной d, между поверхностью плоской отполированной пластинки и соприкасающейся с ней выпуклой поверхностью линзы (рис. 1).

157

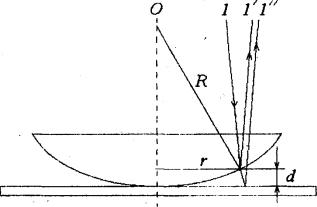
Рисунок 1.

При вычислении оптической разности хода интерферирующих когерентных лучей 1' и 1''можно пренебречь их небольшим наклоном ввиду того, что толщина воздушной прослойки очень мала. Тогда оптическая разность хода (2) этих лучей с учетом потери полуволны при отражении луча 1′′ от более плотной среды

В этом случае линии, которые соответствуют одинаковой разности хода (одинаковой толщине воздушной прослойки) интерферирующих волн, представляют собой концентрические окружности, кольца Ньютона с центром в точке соприкосновения линзы с пластинкой, т.е. интерференционные линии в данном методе - линии равной толщины.

Из рис. 1 имеем r2=R2- (R - d)2 = 2Rd- d2. Учтем, что 2R»d, тогда

158

Найдем радиусы темных rm и светлых rm колец Ньютона при наблюдении в отраженном свете, для чего в (6) подставим вместо последовательно соответствующее значение min (3) и max (2)

При наблюдении колец Ньютона в проходящем свете потеря полуволны для луча 1'' происходит дважды (от поверхностей пластинки и линзы), т.е. оптическая разность хода (4) изменится на целую λ. С учетом этого условия (7) поменяются местами: rmin будет соответствовать радиусам светлых, а rmax’ - радиусам темных колец Ньютона, наблюдаемых в проходящем свете.

Таким образом, измеряя радиусы светлых или темных колец Ньютона при известной длине волны λ падающего света, можно определить радиус кривизны линзы R.

Однако формулы (7) могут дать ошибочный результат, так как вследствие упругой деформации стекла и попадания пылинок в месте соприкосновения может появиться незначительный зазор величиной а. Это приведет к дополнительной разности хода, равной 2а. Тогда

159

условие (3) образования, например, k-го темного кольца в отраженном свете примет вид:

2d+λ/2+2a=(2k+ 1)λ/2 или d= kλ/2 - a.

Подставляя значение d в уравнение (5), имеем

Величина а не может быть измерена непосредственно, но ее можно исключить следующим образом. Запишем выражение (8) для любого другого темного кольца т

Вычитая из (9) выражение (8) получим:

rm2 − rk2 = R(m − k )λ..

Откуда расчетная формула для определения радиуса

кривизны линзы

где m, k – номера темных колец Ньютона; rm , r k - радиусы темных колец Ньютона;

λ- длина волны падающего монохроматического света.

Вприведенных расчетах не учитывается влияние света, отраженного от верхней поверхности линзы и нижней поверхности пластинки. Это делается потому, что толщина центральной части

160