fizpr

Среднюю скорость движения зарядов υ в проводнике получим,

использовав соотношение между силой тока I1, числом зарядов в единице объема образца п и средней скоростью:

I1 = вdneυ

вdne

Подставляя это значение средней скорости в соотношение (1). Получим:

Явление образования поперечного электрического поля и соответствующей ему разности потенциалов Ux в образце, по которому протекает электрический ток, при расположении его в поперечном магнитном поле называется эффектом Холла. Разность потенциалов

Ux носит название холловской разности потенциалов. Величину

R = 1 называют постоянной Холла для данного образца. en

Из формулы (2) получим рабочую формулу для определения постоянной Холла:

Порядок выполнения работы

1.Ознакомиться с рабочей схемой и приборами.

2.С разрешения преподавателя включить питание установки.

111

3.Потенциометром с помощью амперметра А1 установить в образце ток I1 = 3А.

4.В отсутствие магнитного поля определить напряжение U1, между точками а и б, которое появляется в результате того, что практически невозможно закрепить проводники в контактах по эквипотенциальной линии, т.е. чтобы между точками а и б отсутствовала разность потенциалов.

5.Включить ток в электромагните 3, по амперметру А2 определять величину тока I2, по вольтметру V определить соответствующее напряжение U2.

6.Холловскую разность потенциалов Uх в данном эксперименте определяют как разность

U x = U 2 −U1

7.Эксперимент повторить, установив в образце ток I1 = 5 и 7А.

8.Результаты занести в таблицу 1.

9.Отключить питание установки.

10.Определить индукцию магнитного поля В по формуле:

В= μ0 NI2 ,

h

где N – число витков;

h – ширина воздушного зазора электромагниту;

12.Оформить результаты расчета постоянной Холла по методу Стьюдента.

13.Из соотношения, которое определяет величину постоянной Холла

( R = 1 ), найти значение концентрации электронов в образце, en

взяв R как среднее по п.11.

Таблица 1 - Результаты измерений и вычислений

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чем заключается эффект Холла?

2.От чего зависит сила Лоренца?

3.Как определить направление действия силы Лоренца?

4.Как определяется постоянная Холла?

5.О чем говорит знак постоянной Холла?

6.Как вычислить среднюю скорость электрона в образце?

7.Как определить концентрацию электронов в образце?

113

4. КОЛЕБАНИЯ И ВОЛНЫ

Лабораторная работа № 401

ЗНАКОМСТВО С РАБОТОЙ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА. ОПРЕДЕЛЕНИЕ НЕИЗВЕСТНОЙ ЧАСТОТЫ ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ МЕТОДОМ ФИГУР ЛИССАЖУ

Цель работы: ознакомление с работой электронного осциллографа, определение неизвестной частоты сигнала методом фигур Лиссажу.

Приборы и оборудование: электронный осциллограф, генератор звуковой частоты.

Основные требования к теоретической подготовке: При подготовке к данной лабораторной работе необходимо проработать разделы курса общей физики: "Гармонические колебания", "Сложение взаимно перпендикулярных колебаний", а также методические указания к данной работе.

Теория метода и описание установки

1. Устройство и робота электронного осциллографа.

Осциллограф – прибор, который позволяет наблюдать и фотографировать быстротекущие процессы продолжительностью 10-6

– 10 -7 секунды. Электронно-лучевой осциллограф состоит из электронно-лучевой трубки, генератора развертки, двух усилителей и блока питания.

114

Для ознакомления с работой осциллографа разберем назначение каждой его части.

Электронно-лучевая трубка. Важнейшим элементом катодного осциллографа является электронно-лучевая трубка, которая представляет собой стеклянную колбу специальной формы с высоким вакуумом. Электронно-лучевые трубки могут быть двух типов: электростатические и магнитные. В трубках первого типа фокусирование и отклонение луча осуществляются электрическим полем, в трубках второго типа - магнитным.

Электронно-лучевая трубка (рис.1) состоит из электронной пушки (на рисунке выделена пунктиром), испускающей пучок электронов; двух пар отклоняющих пластин Пх и Пу, расположенных во взаимно перпендикулярных плоскостях; и флуоресцирующего экрана ФЭ. Электронная пушка позволяет получить узкий сфокусированный поток электронов. Она состоит из катода К, управляющего электрода УЭ и двух анодов А1 и А2 (А1 – фокусирующий анод, А2 — ускоряющий анод).

Горизонтально расположенные пластины Пу служат для отклонения луча в вертикальном направлении и называются вертикально отклоняющими пластинами. Вторая пара пластин Пх служит для отклонения луча в горизонтальном направлении и называется горизонтально отклоняющими пластинами.

Одновременное действие обеих пар отклоняющих пластин на электронный луч позволяет наблюдать на экране изменение исследуемого напряжения во времени. Пройдя отклоняющие пластины, электронный луч попадает на экран электронно-лучевой трубки, покрытый слоем флуоресцирующего вещества. При ударе об

115

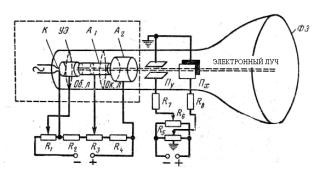
экран электрон приводит в возбужденное состояние атомы и молекулы этого слоя. Возвращаясь в нормальное состояние, атомы и молекулы испускают свет. Это явление носит название люминесценции

Рисунок 1

Генератор развертки. Вторым важным элементом электроннолучевого осциллографа является генератор развертки – радиотехническое устройство, которое позволяет получить напряжение развертки. Генератор развертки позволяет перемещать электронный луч вдоль горизонтальной оси с постоянной скоростью.

Если исследуемое напряжение имеет периодический характер, то для наблюдения на экране формы кривой этого напряжения его подводят к пластинам Пу, а на пластины Пх подают периодическое напряжение, которое называется напряжением развертки.

Для получения на экране неподвижного изображения необходимо, чтобы частоты исследуемого напряжения и напряжения развертки были кратны друг другу. В противном случае изображение на экране осциллографа самопроизвольно будет передвигаться. Перемещение изображения по экрану нежелательно, поскольку

116

затрудняет наблюдение изображения. Для устранения этого недостатка применяется синхронизация частоты генератора с частотой какогонибудь постороннего стабильного источника напряжения. Благодаря синхронизации генератор развертки будет вынужден работать точно с такой же частотой, как и исследуемый сигнал, который вызовет стойкость изображения на экране. Синхронизировать генератор развертки можно или частотой исследуемого напряжения, или частотой переменного напряжения, взятого от сети, или частотой какого-нибудь внешнего напряжения. Для этой цели осциллограф обеспечен переключателем типа синхронизации (переключатель «Синхронизация») и зажимами для подключения внешнего источника напряжения синхронизирующей частоты («Внеш. синхр»).

Блок питания. Блок питания включает ряд устройств, которые обеспечивают энергией электронно-лучевую трубку, генератор развертки, вертикальный и горизонтальный усилители и другие части прибора.

2. Метод фигур Лиссажу.

Используется для определения частоты неизвестного гармонического колебания.

Фигура Лиссажу – это замкнутая траектория точки, которая совершает одновременно два колебания во взаимно перпендикулярных плоскостях.

Чтобы получить уравнение фигуры Лиссажу, рассмотрим результат сложения двух гармонических колебаний одинаковой частоты ω, которые осуществляются вдоль координат OX и OY:

117

x = Α cosωt

оси которого совпадают с осями координат: 118

Если амплитуды колебаний одинаковые, то эллипс (4) превращается в окружность.

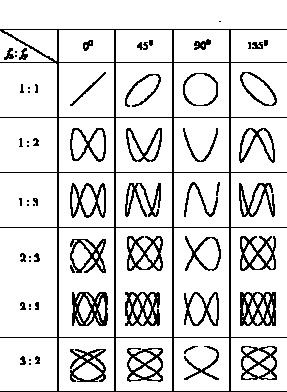
В общем случае форма фигуры Лиссажу зависит от соотношения амплитуд, частот и разности фаз колебаний. При сложении двух взаимно перпендикулярных колебаний с разными частотами получают сложные траектории (рис. 2).

Рисунок 2 119

Фигуры Лиссажу можно наблюдать на экране осциллографа, если на одну пару отклоняющих пластин подать напряжение от звукового генератора, а на другую – напряжение от сети переменного тока. Если соотношение частот этих двух сигналов кратно целому

появляется четкое и неподвижное изображения замкнутой фигуры Лиссажу соответствующей формы (рис.2).

Соотношение частот этих двух сигналов четко определяется соотношением количества точек касания фигуры Лиссажу с координатными осями OX и OY:

Таким образом, если известна одна из двух частот, с помощью

(5) можно определить другую, неизвестную частоту.

Порядок выполнения работы

1.Ознакомиться с рабочей схемой и приборами.

2.Определить, на какую пару (x или y) отклоняющих пластин подается сигнал от генератора (известная частота) и от блока питания (неизвестная частота сигнала).

3.С разрешения преподавателя включить питание установки.

4.Вращая ручку настройки частоты генератора, получить на экране неподвижное изображение любой фигуры Лиссажу.

5.Занести в таблицу изображение фигуры, количество точек касания

фигуры (nx и ny), частоту ν (с генератора), при которой получена

120